Tutorial 10 – 百折不挠:强化学习(Reinforcement Learning)
 Deep Learning
Deep Learning
create by Deepfinder
 Agenda
Agenda
- 师徒相授:有监督学习(Supervised Learning)
- 见微知著:无监督学习(Un-supervised Learning)
- 无师自通:自监督学习(Self-supervised Learning)
- 以点带面:半监督学习(Semi-supervised learning)
- 明辨是非:对比学习(Contrastive Learning)
- 举一反三:迁移学习(Transfer Learning)
- 针锋相对:对抗学习(Adversarial Learning)
- 众志成城:集成学习(Ensemble Learning)
- 殊途同归:联邦学习(Federated Learning)
- 百折不挠:强化学习(Reinforcement Learning)
- 求知若渴:主动学习(Active Learning)
- 万法归宗:元学习(Meta-Learning)
 强化学习的基本原理
强化学习的基本原理
在这个不断进步的技术世界中,强化学习(Reinforcement Learning, RL)作为机器学习的一个重要分支,正迅速发展成为理解人工智能(AI)和机器学习领域的关键。与传统的机器学习方法相比,强化学习独特地专注于学习如何基于环境的反馈作出最优决策。这种方法在多种复杂的、需要连续决策的问题中显示出巨大潜力,从而在近年来获得了显著的关注。 强化学习不仅为机器提供了学习如何在复杂环境中作出决策的能力,而且它的应用正在改变我们的世界。
- 它在许多领域中都发挥着重要作用,例如:
- 机器人技术:让机器人学习如何执行复杂任务,如行走或抓取。
- 游戏:AI玩家学习如何在复杂游戏中击败人类对手。
- 自动驾驶汽车:自动驾驶技术的核心之一,使汽车能够在复杂的道路环境中做出快速反应。
- 个性化推荐系统:基于用户行为和偏好的动态调整。
- 随着技术的不断进步和创新,强化学习在未来可能会有更加广泛的应用场景:
- 智能电网:优化能源分配和消耗,实现更高效的电力管理。
- 医疗保健:协助医生做出更准确的诊断和治疗决策。
- 智能城市:在城市规划和管理中,优化交通流量和公共服务。
- 金融领域:在投资和风险管理中做出更精确的预测和决策。
 强化学习基本概念
强化学习基本概念
- 智能体(Agent):在强化学习(RL)框架中,智能体是指一个能够观察并与环境交互的实体。它通过执行动作并根据环境反馈(通常是奖励信号)来做出决策的系统。智能体的目标是学习如何选择动作以最大化长期累计奖励。
- 环境(Environment):环境是智能体所处的外部系统,它定义了问题的界限和规则。在强化学习中,环境接收智能体的动作并响应给出新的状态和奖励,这决定了智能体的学习过程。
- 状态(State,s):状态是对环境在特定时刻的描述或观察。它通常被视为智能体用来做出决策的信息集合。状态必须包含关于环境的足够信息,以便智能体能够有效地做出行动选择。
- 状态的概率密度函数(State Probability Density Function):状态的概率密度函数是一个数学函数,用于描述在给定当前状态和智能体的动作下,环境转移到各个可能下一状态的概率分布。这个函数是理解和预测环境动态的核心要素。
- 状态价值函数(State Value Function, V(s)):状态价值函数是一个函数,它给出了在策略π下,从状态s开始并遵循该策略所能获得的预期回报的估计值。状态价值函数是用于评估在某状态下开始并遵循特定策略所能达到的长期表现。
- 策略(Policy, π):策略是从状态到动作的映射。在确定性策略中,它定义了在给定状态下智能体将要执行的动作;在随机性策略中,它定义了在给定状态下选择每个可能动作的概率。
- 动作(Action,a):动作是智能体可以在给定状态下选择执行的任何操作。动作根据环境的反馈影响智能体所处的状态以及它接收到的累计回报。
- 动作的概率密度函数(Action Probability Density Function):这个函数描述了在给定状态和策略下,选择每个可能动作的概率分布。特别是在连续动作空间中,这个函数定义了所有可能动作的概率密度。
- 动作价值函数(Action-Value Function, Q(s,a)):动作价值函数或Q函数,给出了在策略π下,从状态s开始并采取动作a,然后遵循策略π所能获得的预期回报的估计值。它是评估在特定状态下执行特定动作并随后遵循特定策略的长期表现的关键。
- 回报(Reward):回报是环境根据智能体执行的动作给出的立即反馈。它是强化学习过程中引导智能体学习和行动选择的关键信号。

- 累计回报(Cumulative Reward):累计回报是从当前时刻开始到未来某个时间点或时序结束时,智能体获得的回报之和。它是强化学习中最关注的优化目标,智能体的学习和决策旨在最大化这个累计值。
- 探索(Exploration):探索是智能体尝试未知或较少尝试动作的过程,目的是发现更有价值的行动选择或信息,以改善其决策策略。
- 利用(Exploitation):利用是指智能体选择那些已知为产生最大回报的动作的过程。在利用中,智能体依赖已有知识做出决策,而非寻求新的信息。
- 轨迹(Trajectory):在强化学习中,轨迹是指智能体在与环境交互过程中经历的一系列状态(s)、动作(a)和奖励(r)的序列。
理解强化学习中的随机性
在强化学习(Reinforcement Learning, RL)中,随机性(或不确定性)是一个核心概念,它出现在各个方面,包括环境的动态特性、智能体的策略、学习过程和奖励信号等。理解和处理这些随机性对于设计有效的RL算法至关重要。以下详细介绍强化学习中的随机性:
- 环境的随机性
- 状态转移的随机性: 在大多数强化学习问题中,环境的状态转移可能具有随机性。即当智能体在某状态下执行一个动作时,它可能以一定的概率转移到多个不同的后续状态。
- 奖励的随机性: 在某些RL问题中,即使在相同的状态和动作下,每次得到的奖励也可能有所不同,反映了环境中的不确定性或噪声。
- 策略的随机性:
- 探索与利用:在强化学习中,智能体需要在探索(尝试新的或少见的行动以获得更多信息)和利用(根据已有知识选择最佳行动)之间找到平衡。 探索通常涉及随机性,例如,智能体可能会以一定的概率随机选择一个动作,而不是总是选择当前看来最佳的动作。
- 随机策略: 在某些算法中,如策略梯度方法,策略本身可能是随机的,意味着即使在相同的状态下,智能体也可能以一定的概率选择不同的动作。
- 学习过程的随机性:
- 初始化:强化学习算法的性能可能受到初始条件的影响,比如神经网络权重的初始随机赋值。 另外,在使用经验回放(如DQN中)的学习过程中,从经验缓冲池中随机抽取样本也引入了随机性。
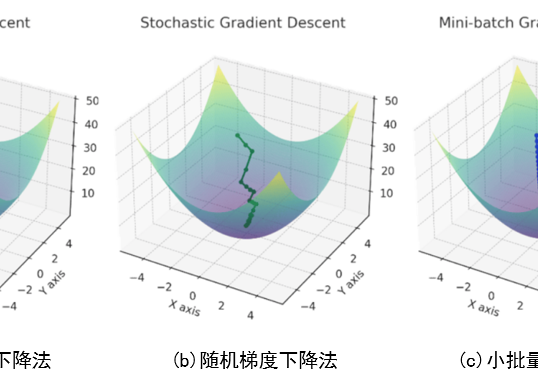
- 随机梯度下降(Stochastic Gradient Descent, SGD):在基于梯度的学习方法中,梯度的估计通常基于随机选择的样本,而非全体数据集,这也引入了随机性。
- 强化学习中的随机性是双刃剑:
- 一方面它增加了学习过程的复杂性和挑战;
- 另一方面,适当的随机性有助于智能体探索环境,避免陷入局部最优。
- 因此,合理地理解和利用随机性是设计高效强化学习系统的关键。
 基于价值的深度强化学习(DQN)
基于价值的深度强化学习(DQN)
要理解DQN,我们首先需要理解Q值。Q值是一个函数,Q(s, a)表示在状态s下执行动作a可以得到的预期奖励。
直观上讲,Q值告诉智能体哪些动作在长期来看更有利。
Q学习的目标是找到最优的Q值函数,从而智能体可以通过查看Q值来选择最佳动作。
如何找到Q函数?
深度学习的魅力就是遇到解决不了的问题直接扔给神经网络进行学习即可。
在DQN中,我们使用一个深度神经网络来预测Q值,网络的输入是状态,输出是每个动作的Q值。
- 想象一下,有一个机器人(智能体)在玩一个游戏。
- 它的目标是获取尽可能多的分数(奖励)。游戏中的每个场景可以视为一个“状态”,机器人可以采取各种动作(比如向左走、向右走)。
- 在DQN中,我们让机器人自己学习。机器人会尝试不同的动作,并观察哪些动作带来更高的分数。
- 在传统强化学习方法中,机器人有一个记分板(Q表),上面记录了在每个场景(状态)中采取不同动作可能获得的分数。即Sarsa算法。
- 在游戏变得非常复杂时,记分板(Q表)变得非常大,机器人不可能记住所有的信息。
- 在DQN中,我们用一个神经网络来帮助机器人估计这个记分板上的分数,即Q值。神经网络试图预测在特定状态下采取特定动作能得到的分数(Q值)。
问题来了,如何使得神经网络使其预测的Q值尽可能接近真实的Q值?
注意,因为环境的复杂性和不确定性。这些Q值通常不能直接计算,而是需要通过与环境的交互来逐渐估计和逼近。
贝尔曼方程和时序差分学习是解决这问题的关键。
贝尔曼方程与时序差分学习(TD-Learning)
- 贝尔曼方程是强化学习中的一个核心概念。
- 贝尔曼方程基于马尔可夫决策过程(MDP),它提供了一种计算当前状态价值或动作价值(考虑未来奖励)的递归方法。
- 递归的思想是将一个大问题分解为相似的小问题。
- 在这里,贝尔曼方程将一个长期的序列决策问题分解为一步决策问题和剩余的序列决策问题。对于动作价值函数$Q(s, a)$ , 贝尔曼方程可以表示为:
$$
Q(s, a)=\mathbb{E}\left[R_{t+1}+\gamma \max _{a^{\prime}} Q\left(S_{t+1}, a^{\prime}\right) \mid S_t=s, A_t=a\right]
$$
这里, $\mathbb{E}[\cdot]$ 表示期望值, $R_{t+1}$ 是奖励, $\gamma$ 是折扣因子,用来衡量未来奖励的当前价值。这里有几个要点:
- 即时奖励 $R_{t+1}$ : 表示在状态 $s$ 下执行动作 $a$ 之后智能体立即获得的奖励。
- 折扣未来奖励 $\gamma \max _{d^{\prime}} Q\left(S_{t+1}, a^{\prime}\right)$ : 代表智能体预期在下一个状态 $S_{t+1}$ 采取最佳动作 $a^{\prime}$ 能够获得的折扣后的未来回报。这里, $\gamma$ (折扣因子)确保了未来的奖励相比于即时奖励的重要性降低。这是一个符合常理的设定,就像现实生活中,十年后给你一百块带来的期望肯定远远小于即可给你一百块钱带来的期望。
- 期望值 $\mathbb{E}[\cdot]$ : 因为环境的不确定性或策略的随机性,贝尔曼方程使用期望值来综合所有可能的下一状态和奖励,确保智能体的决策考虑了所有可能的未来情景。
在贝尔曼方程中,期望 $\mathbb{E}[\cdot]$ 是关于环境动态(即从状态 $s$ 通过动作 $a$ 转移到下一个状态 $s^{\prime}$ 并获得奖励 $R_{t+1}$ ) 的统计平均。
这个期望的准确计算通常需要环境的完整模型 (即状态转移概率和奖励函数),这在很多实际应用中是未知的或者难以精确获得的。
这主要是因为几个原因
- 环境的不确定性
- 状态空间
- 动作空间的庞大
- 模型的未知性
这些因素使得直接计算贝尔曼方程中的期望值变得不切实际或计算上不可行,因此我们采用时序差分 (TD) 学习方法来估计这个值。
具体来说,TD学习简化了贝尔曼方程,不必计算期望,直接使用当前估计和下一个状态(或下一个几个状态)的奖励来更新价值估计,其更新规则可以表述为:
$$
Q\left(S_t, A_t\right) \leftarrow Q\left(S_t, A_t\right)+\alpha\left[R_{t+1}+\gamma \max _{a^{\prime}} Q\left(S_{t+1}, a^{\prime}\right)-Q\left(S_t, A_t\right)\right]
$$
这里:
- $-\alpha$ 是学习率。
- $-R_{t+1}+\gamma \max _{a^{\prime}} Q\left(S_{t+1}, a^{\prime}\right)$ 是TD目标, 代表了对下一个状态的价值的估计。这个估计方法肯定比直接估计下一个状态的价值要准确,因为当前的价值 $R_{t+1}$ 是已经观测到的。
- 这就像你从家出发上学的途中有一个商店,当你走到商店时再预估到达学校的时间,肯定比刚从家出发就预测到校时间要准确,因为从家到商店的时间已经被观察到了。
- TD目标那么这个值怎么得到呢?
- 在深度强化学习(如DQN)中,神经网络被用来逼近Q函数。网络的输入是状态(以及可能的动作),输出是该状态(和动作)的Q值估计。
- 因此,在任意时刻,下一状态的价值实际上是由神经网络基于其当前的参数估计得出的。
- 实际上,这个TD目标就是我们在训练神经网络时的标签。
- $-R_{t+1}+\gamma \max _{a^{\prime}} Q\left(S_{t+1}, a^{\prime}\right)-Q\left(S_t, A_t\right)$ 是TD误差,表示当前奖励加上下一个状态的折现后的估计价值与当前状态的估计价值之间的差异。这里记作 $\delta_t$
- 更新 $\mathrm{Q}$ 值的基本思想是:
- 如果我们在某个状态动作对 $\left(S_t, A_t\right)$ 得到的奖励比我们原本预期的要多,那么我们应该增加这个状态动作对的 $Q$ 值。
- 反之,如果得到的奖励比预期的少,我们应该减少这个状态动作对的 $Q$值。
- 因此,TD学习中的 $Q$ 值更新公式为:
$$
Q\left(S_t, A_t\right) \leftarrow Q\left(S_t, A_t\right)+\alpha \times \delta_t
$$
- 这里, $\alpha$ 是学习率,它决定了我们在每次更新时要改变多少 $\mathrm{Q}$ 值。
- 理解这个更新过程如果 $\delta_t$ 为正 (实际获得的奖励加上对未来奖励的估计超过了当前 $Q$ 值的估计),我们提高 $Q\left(S_t, A_t\right)$ 。
- 如果 $\delta_t$ 为负(实际获得的奖励加上对未来奖励的估计低于当前 $\mathrm{Q}$ 值的估计),我们降低 $Q\left(S_t, A_t\right)$ 。
通过这种方式,TD学习算法能够不断地调整其对每个状态-动作对价值的估计,以更好地适应和学习环境的动态特性。
注意, $Q$ 值的更新并不直接等同于监督学习中的损失函数。
$Q$ 值的更新更像是一种迭代式的价值估计过程,通过不断基于TD误差的校正,使得预测的 $Q$ 值更接近于真实(或最优)的 $Q$ 值。
可以说,在训练的每个步骤中,TD更新的目标 $Q$ 值充当了类似于监督学习中真实标签的角色,
但这个“标签”本身也是在不断学习和调整中的,没有像监督学习中那样固定不变的“真实标签”。
训练神经网络
- 如何训练这个神经网络来预测Q值?
- 训练神经网络的首要步骤是数据收集。
- 强化学习中的数据通常由智能体在与环境交互过程中所获得的状态、动作、奖励和下一个状态组成。
- 这些数据被存储在经验回放缓冲区内,以供后续训练使用。
- 接下来进行抽样,神经网络的训练涉及从经验回放缓冲区中随机抽取一批样本。这样做有助于减少样本数据间的相关性,进而降低训练过程的方差。
- 对于每个抽样出的样本,我们根据TD目标和网络的当前预测计算损失。其目的是最小化预测Q值和TD目标之间的差距,公式如下:
$$
\operatorname{LossMSE}=\frac{1}{N} \sum_{i=1}^N\left(y_i-Q\left(s_i, a_i ; \theta\right)\right)^2
$$
其中:
- $-N$ 是样本数量。
- $-y_i$ 是第 $i$ 个样本的TD目标值,根据贝尔曼方程计算得出。
- $-Q\left(s_i, a_i ; \theta\right)$ 是神经网络关于当前参数 $\theta$ 下,状态 $s_i$ 和动作 $a_i$ 的预测 $\mathrm{Q}$ 值。
在训练过程中,通过梯度下降方法最小化MSE,以此调整网络参数 $\theta$ ,使得预测的 $\mathrm{Q}$ 值 $Q(s, a ; \theta)$ 接近TD 目标 $y$ ,即减少神经网络输出与期望输出之间的误差。
整个训练过程是一个持续的迭代过程,直至达到既定的性能标准或完成预没的训练周期。
在此过程中,应注意保持探索与利用之间的平衡。智能体不仅要利用现有策略来最大化即时奖励,还应不断探索新的策略,以发现可能获得更高长期回报的行为模式。
评估网络与目标网络
- $R_{t+1}+\gamma \max _{a^{\prime}} Q\left(S_{t+1}, a^{\prime}\right)$ 是TD目标
- 在DQN中,神经网络被用来逼近 $\mathrm{Q}$ 函数。网络的输入是状态(以及可能的动作),输出是该状态(和动作)的 $\mathrm{Q}$ 值估计。
- 因此,在任意时刻,下一状态的价值 $Q\left(S_{t+1}, a^{\prime}\right)$ 实际上是由神经网络基于其当前的参数估计得出的。
- 这是一种自举的方式,单个网络同时进行 $Q$ 值的估计和TD目标的计算,会导致一种“追逐自己尾巴”的情况,其中 $Q$ 值的更新可能过于频繁和剧烈。
- 这种情况下,网络试图在一个连续变化的目标上进行训练,很难收敛,容易造成训练过程的不稳定性和振荡。
- 为了解决这个问题,在DQN (Deep Q-Networks) 及其变体中,一般使用两种神经网络一一评估网络和目标网络。
评估网络(也称为策略网络)用于实时估计值函数。换句话说,这个网络负责根据当前状态和动作,预测Q值。在学习过程中,此网络的参数不断更新以反映最新学习的结果。
目标网络在结构上与评估网络相同,但其参数更新频率较低。目标网络的主要作用是在计算TD目标(Temporal-Difference Target)时提供一个相对稳定的Q值估计。这个TD目标通常用于计算损失函数和进行梯度下降。
由于目标网络的更新滞后于评估网络,它可以为学习过程提供一个较为稳定的学习目标。这有助于减少每次更新所带来的方差,从而使训练过程更加平滑。而且,分离的目标网络可以在一定程度上防止过拟合。因为目标网络不会立即反映出最新的学习成果,从而避免了评估网络可能因过度适应最近的经验而忽略了长期的策略。
注意,目标网络的参数不是每次迭代都更新。通常,它的参数会在固定的时间步或者固定的训练周期后从评估网络复制过来。这个更新间隔是一个超参数,需要根据具体的应用场景和任务来调整。
探索(exploration)和利用(exploitation)
Epsilon-greedy策略是强化学习中的一种基本策略,用于平衡探索和利用。其基本原理是:
- 以概率epsilon选择一个随机动作(探索)。
- 以概率1-epsilon选择当前最优动作(利用)。
通过调整epsilon值,可以控制智能体的探索和利用行为:
- 在训练初期,epsilon值较高,智能体更多地进行探索,尝试不同的动作。
- 在训练后期,epsilon值较低,智能体更多地利用已经学到的知识,选择最优动作。
指数衰减
采用指数衰减更新epsilon值,使得epsilon值从初始值逐渐减小到最终值。这种方式可以平滑地过渡智能体的行为:
- 在训练初期,智能体主要进行探索,以便更好地了解环境。
- 随着训练的进行,智能体逐渐减少探索,更多地利用已学得的知识进行决策。
import matplotlib.pyplot as plt
import numpy as np
# 参数定义
epsilon_start = 1.0
epsilon_end = 0.01
epsilon_decay = 500
sample_count = np.arange(0, 2000) # 2000步采样次数
# 计算每个采样点的epsilon值
epsilon_values = epsilon_end + (epsilon_start - epsilon_end) * np.exp(-1. * sample_count / epsilon_decay)
# 绘制epsilon值的变化曲线
plt.plot(sample_count, epsilon_values)
plt.xlabel('Sample Count')
plt.ylabel('Epsilon Value')
plt.title('Epsilon Decay Over Time')
plt.grid(True)
plt.show()
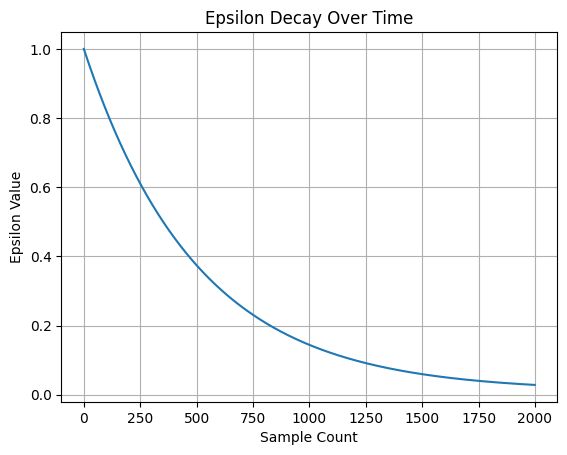
这种动态调整探索和利用的策略有助于智能体在早期充分探索环境,后期充分利用学到的策略,提高训练效果和效率。
 GYM库
GYM库
- Gym 是一个用于开发和比较强化学习算法的开源工具包,由 OpenAI 提供。
- 它提供了一系列标准化的环境,这些环境涵盖了多种不同类型的问题,方便研究人员和开发者进行算法开发、测试和比较。
- Gym 库不仅支持经典的控制和博弈问题,还支持一些复杂的任务。例如:
- CartPole-v1: 经典的平衡杆问题。
- MountainCar-v0: 一个小车需要爬上山顶。
- Acrobot-v1: 一个两连杆机器人需要通过摆动达到特定高度。
- Pong-v0: 乒乓球游戏。
- Breakout-v0: 打砖块游戏。
- SpaceInvaders-v0: 太空侵略者游戏。
- LunarLander-v2: 月球着陆器。
- BipedalWalker-v2: 两足机器人行走。
- Humanoid-v2: 模拟人形机器人。
- Ant-v2: 四足机器人。
- FetchReach-v1: Fetch 机器人控制任务。
Gym库的详细文档和环境列表可以在其官方网站上找到:Gym Documentation
Humanoid示例如下:

cart_pole示例如下:
本项目也是在此游戏环境下进行的代码示例。
 示例代码:基于价值的强化学习
示例代码:基于价值的强化学习
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import numpy as np
import random
import math
import gym
# 定义重放缓冲区类,用于存储经验
class ReplayBuffer:
# 初始化方法,定义缓冲区容量和位置
def __init__(self, capacity):
self.buffer = []
self.capacity = capacity
self.position = 0
# 向缓冲区添加经验
def push(self, transition):
if len(self.buffer) < self.capacity:
self.buffer.append(None)
self.buffer[self.position] = transition
self.position = (self.position + 1) % self.capacity
# 从缓冲区随机采样一个批次的经验
def sample(self, batch_size):
batch = random.sample(self.buffer, batch_size)
state, action, reward, next_state, done = map(np.stack, zip(*batch))
return state, action, reward, next_state, done
# 返回缓冲区的当前大小
def __len__(self):
return len(self.buffer)
# 定义策略网络类
class PolicyNetwork(nn.Module):
def __init__(self, n_states, n_actions):
super(PolicyNetwork, self).__init__()
self.fc1 = nn.Linear(n_states, 128)
self.fc2 = nn.Linear(128, n_actions)
def forward(self, x):
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
# 定义深度Q网络类
class DQN:
# 初始化方法,定义相关参数和网络
def __init__(self, model, memory, cfg):
self.n_actions = cfg['n_actions'] # 动作数量
self.device = torch.device(cfg['device']) # 设备(CPU或GPU)
self.gamma = cfg['gamma'] # 折扣因子
self.sample_count = 0 # 采样计数
self.epsilon = cfg['epsilon_start'] # 初始epsilon值
self.epsilon_start = cfg['epsilon_start'] # epsilon初始值
self.epsilon_end = cfg['epsilon_end'] # epsilon最终值
self.epsilon_decay = cfg['epsilon_decay'] # epsilon衰减率
self.batch_size = cfg['batch_size'] # 批量大小
self.policy_net = model.to(self.device) # 策略网络
self.target_net = model.to(self.device) # 目标网络
# 初始化目标网络权重与策略网络相同
for target_param, param in zip(self.target_net.parameters(), self.policy_net.parameters()):
target_param.data.copy_(param.data)
self.optimizer = optim.Adam(self.policy_net.parameters(), lr=cfg['lr']) # 优化器
self.memory = memory # 重放缓冲区
# 采样动作方法,基于epsilon-greedy策略
def sample_action(self, state):
self.sample_count += 1 # 增加采样计数
# 更新epsilon值,采用指数衰减
self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * \
math.exp(-1. * self.sample_count / self.epsilon_decay)
if random.random() > self.epsilon: # 选择贪婪策略
with torch.no_grad():
state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
q_values = self.policy_net(state) # 计算Q值
action = q_values.max(1)[1].item() # 选择Q值最大的动作
else: # 随机选择动作
action = random.randrange(self.n_actions)
return action # 返回动作
# 预测动作方法,用于测试阶段
@torch.no_grad()
def predict_action(self, state):
state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
q_values = self.policy_net(state) # 计算Q值
action = q_values.max(1)[1].item() # 选择Q值最大的动作
return action # 返回动作
# 更新网络方法
def update(self):
if len(self.memory) < self.batch_size: # 如果缓冲区中的经验不足一个批次
return
# 从缓冲区采样一个批次的经验
state_batch, action_batch, reward_batch, next_state_batch, done_batch = self.memory.sample(self.batch_size)
# 转换为张量
state_batch = torch.tensor(np.array(state_batch), device=self.device, dtype=torch.float)
action_batch = torch.tensor(action_batch, device=self.device).unsqueeze(1)
reward_batch = torch.tensor(reward_batch, device=self.device, dtype=torch.float)
next_state_batch = torch.tensor(np.array(next_state_batch), device=self.device, dtype=torch.float)
done_batch = torch.tensor(np.float32(done_batch), device=self.device)
# 计算当前Q值
q_values = self.policy_net(state_batch).gather(dim=1, index=action_batch)
# 计算下一个状态的Q值
next_q_values = self.target_net(next_state_batch).max(1)[0].detach()
# 计算期望Q值
expected_q_values = reward_batch + self.gamma * next_q_values * (1 - done_batch)
# 计算损失
loss = nn.MSELoss()(q_values, expected_q_values.unsqueeze(1))
self.optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播
# 梯度裁剪
for param in self.policy_net.parameters():
param.grad.data.clamp_(-1, 1)
self.optimizer.step() # 更新网络参数
# 环境和智能体配置函数
def env_agent_config(cfg):
env = gym.make(cfg['env_name']) # 创建环境
n_states = env.observation_space.shape[0] # 状态空间维度
n_actions = env.action_space.n # 动作空间维度
memory = ReplayBuffer(cfg['memory_capacity']) # 创建重放缓冲区
agent = DQN(PolicyNetwork(n_states, n_actions), memory, cfg) # 创建DQN智能体
return env, agent # 返回环境和智能体
# 训练函数
def train(cfg, env, agent):
print("开始训练!")
rewards = [] # 存储每回合的奖励
steps = [] # 存储每回合的步数
for i_ep in range(cfg['train_eps']):
ep_reward = 0 # 初始化回合奖励
ep_step = 0 # 初始化回合步数
state, _ = env.reset() # 重置环境,获取初始状态
for _ in range(cfg['ep_max_steps']):
ep_step += 1
action = agent.sample_action(state) # 采样动作
next_state, reward, done, truncated, info = env.step(action) # 执行动作
done = done or truncated
agent.memory.push((state, action, reward, next_state, done)) # 将经验存储到缓冲区
state = next_state # 更新状态
agent.update() # 更新评估网络
ep_reward += reward # 累加奖励
if done: # 如果回合结束
break
if (i_ep + 1) % cfg['target_update'] == 0: # 每隔一定回合更新目标网络
agent.target_net.load_state_dict(agent.policy_net.state_dict())
steps.append(ep_step) # 记录步数
rewards.append(ep_reward) # 记录奖励
if (i_ep + 1) % 10 == 0:
print(f"回合:{i_ep + 1}/{cfg['train_eps']},奖励:{ep_reward:.2f},Epislon:{agent.epsilon:.3f}")
print("完成训练!")
env.close() # 关闭环境
return {'rewards': rewards} # 返回奖励记录
# 测试函数
def test(cfg, env, agent):
print("开始测试!")
rewards = [] # 存储每回合的奖励
steps = [] # 存储每回合的步数
for i_ep in range(cfg['test_eps']):
ep_reward = 0 # 初始化回合奖励
ep_step = 0 # 初始化回合步数
state, _ = env.reset() # 重置环境,获取初始状态
done = False # 初始化结束标志
while not done and ep_step < cfg['ep_max_steps']:
ep_step += 1
action = agent.predict_action(state) # 预测动作
next_state, reward, done, truncated, info = env.step(action) # 执行动作
done = done or truncated
state = next_state # 更新状态
ep_reward += reward # 累加奖励
if done:
print(f"回合 {i_ep + 1} 在步数 {ep_step} 完成")
steps.append(ep_step) # 记录步数
rewards.append(ep_reward) # 记录奖励
print(f"回合:{i_ep + 1}/{cfg['test_eps']},奖励:{ep_reward:.2f}")
print("完成测试")
env.close() # 关闭环境
return {'rewards': rewards} # 返回奖励记录
# 获取配置参数函数
def get_args():
return {
'env_name': 'CartPole-v1', # 环境名称
'n_actions': 2, # 动作数量
'device': 'cpu', # 设备(CPU)
'gamma': 0.99, # 折扣因子
'epsilon_start': 1.0, # 初始epsilon值
'epsilon_end': 0.01, # 最终epsilon值
'epsilon_decay': 500, # epsilon衰减率
'batch_size': 64, # 批量大小
'lr': 0.001, # 学习率
'memory_capacity': 10000, # 缓冲区容量
'train_eps': 100, # 训练回合数
'test_eps': 100, # 测试回合数
'ep_max_steps': 200, # 每回合最大步数
'target_update': 10, # 目标网络更新频率
'seed': 42 # 随机种子
}
# 绘制奖励曲线函数
def plot_rewards(rewards, cfg, tag="train"):
import matplotlib.pyplot as plt
plt.plot(rewards) # 绘制奖励曲线
plt.title(f'{tag} Rewards') # 设置标题
plt.show() # 显示图像
# 获取参数
cfg = get_args()
# 训练
env, agent = env_agent_config(cfg)
res_dic = train(cfg, env, agent)
# 绘制训练奖励曲线
plot_rewards(res_dic['rewards'], cfg, tag="train")
# 测试
res_dic = test(cfg, env, agent)
# 绘制测试奖励曲线
plot_rewards(res_dic['rewards'], cfg, tag="test")
开始训练!
/home/arwin/anaconda3/envs/dt/lib/python3.8/site-packages/gym/utils/passive\_env\_checker.py:233: DeprecationWarning: np.bool8 is a deprecated alias for np.bool\_. (Deprecated NumPy 1.24) if not isinstance(terminated, (bool, np.bool8)): 回合:10/100,奖励:11.00,Epislon:0.586 回合:20/100,奖励:16.00,Epislon:0.401 回合:30/100,奖励:20.00,Epislon:0.290 回合:40/100,奖励:46.00,Epislon:0.152 回合:50/100,奖励:60.00,Epislon:0.059 回合:60/100,奖励:100.00,Epislon:0.027 回合:70/100,奖励:138.00,Epislon:0.014 回合:80/100,奖励:162.00,Epislon:0.010 回合:90/100,奖励:200.00,Epislon:0.010 回合:100/100,奖励:200.00,Epislon:0.010 完成训练!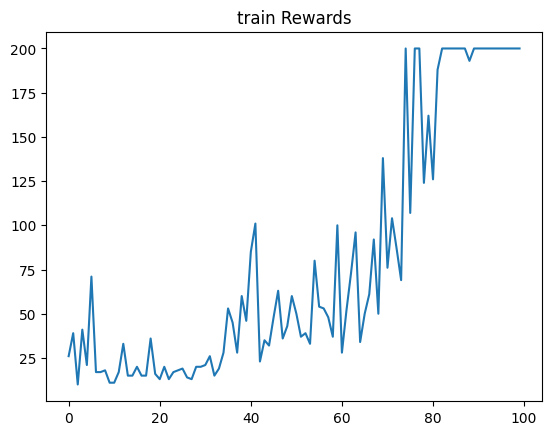
开始测试!
回合 1 在步数 190 完成
回合:1/100,奖励:190.00
回合:2/100,奖励:200.00
回合:3/100,奖励:200.00
回合 4 在步数 175 完成
回合:4/100,奖励:175.00
回合 5 在步数 199 完成
回合:5/100,奖励:199.00
回合 6 在步数 175 完成
回合:6/100,奖励:175.00
回合:7/100,奖励:200.00
回合:8/100,奖励:200.00
回合:9/100,奖励:200.00
回合:10/100,奖励:200.00
回合:11/100,奖励:200.00
回合 12 在步数 188 完成
回合:12/100,奖励:188.00
回合:13/100,奖励:200.00
回合:14/100,奖励:200.00
回合 15 在步数 197 完成
回合:15/100,奖励:197.00
回合:16/100,奖励:200.00
回合:17/100,奖励:200.00
回合:18/100,奖励:200.00
回合:19/100,奖励:200.00
回合:20/100,奖励:200.00
回合 21 在步数 184 完成
回合:21/100,奖励:184.00
回合:22/100,奖励:200.00
回合 23 在步数 187 完成
回合:23/100,奖励:187.00
回合:24/100,奖励:200.00
回合 25 在步数 194 完成
回合:25/100,奖励:194.00
回合:26/100,奖励:200.00
回合:27/100,奖励:200.00
回合 28 在步数 196 完成
回合:28/100,奖励:196.00
回合:29/100,奖励:200.00
回合 30 在步数 199 完成
回合:30/100,奖励:199.00
回合:31/100,奖励:200.00
回合:32/100,奖励:200.00
回合:33/100,奖励:200.00
回合 34 在步数 188 完成
回合:34/100,奖励:188.00
回合 35 在步数 190 完成
回合:35/100,奖励:190.00
回合:36/100,奖励:200.00
回合:37/100,奖励:200.00
回合:38/100,奖励:200.00
回合 39 在步数 192 完成
回合:39/100,奖励:192.00
回合 40 在步数 191 完成
回合:40/100,奖励:191.00
回合:41/100,奖励:200.00
回合 42 在步数 185 完成
回合:42/100,奖励:185.00
回合:43/100,奖励:200.00
回合 44 在步数 184 完成
回合:44/100,奖励:184.00
回合:45/100,奖励:200.00
回合 46 在步数 192 完成
回合:46/100,奖励:192.00
回合:47/100,奖励:200.00
回合:48/100,奖励:200.00
回合:49/100,奖励:200.00
回合:50/100,奖励:200.00
回合:51/100,奖励:200.00
回合:52/100,奖励:200.00
回合:53/100,奖励:200.00
回合 54 在步数 194 完成
回合:54/100,奖励:194.00
回合 55 在步数 181 完成
回合:55/100,奖励:181.00
回合:56/100,奖励:200.00
回合:57/100,奖励:200.00
回合 58 在步数 185 完成
回合:58/100,奖励:185.00
回合:59/100,奖励:200.00
回合 60 在步数 177 完成
回合:60/100,奖励:177.00
回合 61 在步数 176 完成
回合:61/100,奖励:176.00
回合:62/100,奖励:200.00
回合:63/100,奖励:200.00
回合:64/100,奖励:200.00
回合:65/100,奖励:200.00
回合:66/100,奖励:200.00
回合 67 在步数 185 完成
回合:67/100,奖励:185.00
回合 68 在步数 200 完成
回合:68/100,奖励:200.00
回合:69/100,奖励:200.00
回合:70/100,奖励:200.00
回合:71/100,奖励:200.00
回合 72 在步数 185 完成
回合:72/100,奖励:185.00
回合:73/100,奖励:200.00
回合:74/100,奖励:200.00
回合:75/100,奖励:200.00
回合:76/100,奖励:200.00
回合:77/100,奖励:200.00
回合 78 在步数 191 完成
回合:78/100,奖励:191.00
回合 79 在步数 173 完成
回合:79/100,奖励:173.00
回合 80 在步数 188 完成
回合:80/100,奖励:188.00
回合:81/100,奖励:200.00
回合:82/100,奖励:200.00
回合:83/100,奖励:200.00
回合:84/100,奖励:200.00
回合:85/100,奖励:200.00
回合 86 在步数 192 完成
回合:86/100,奖励:192.00
回合:87/100,奖励:200.00
回合:88/100,奖励:200.00
回合 89 在步数 190 完成
回合:89/100,奖励:190.00
回合 90 在步数 180 完成
回合:90/100,奖励:180.00
回合:91/100,奖励:200.00
回合 92 在步数 197 完成
回合:92/100,奖励:197.00
回合 93 在步数 195 完成
回合:93/100,奖励:195.00
回合:94/100,奖励:200.00
回合:95/100,奖励:200.00
回合 96 在步数 189 完成
回合:96/100,奖励:189.00
回合 97 在步数 192 完成
回合:97/100,奖励:192.00
回合:98/100,奖励:200.00
回合:99/100,奖励:200.00
回合:100/100,奖励:200.00
完成测试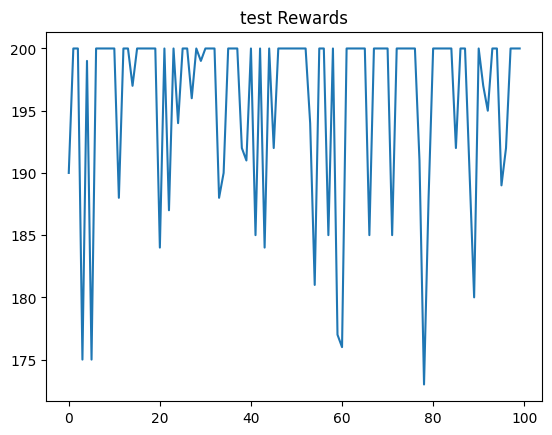
 基于策略的深度强化学习(Policy-based model)
基于策略的深度强化学习(Policy-based model)
- 想象一下,你正在教一个机器人学习如何走路。
- 在基于策略的强化学习方法中,你直接告诉这个机器人在每一步该如何行动。这种指导是通过一个概率模型来实现的,即策略函数。
- 策略函数考虑当前的环境(即机器人的当前状态),然后输出每一个可能动作的概率。机器人根据这些概率来选择其动作。
- 因此,在每个状态下,机器人有一个清晰的概率指导它决定下一步如何行动。
- 这种方法的关键优势是可以处理更加复杂和多样的动作选择,例如在连续动作空间中选择合适的动作力度和方向。
相比之下,在DQN这类基于值的强化学习方法中,我们不是直接告诉机器人每一步怎么做,而是给它一个评分系统:对于每一个可能的动作,DQN评估其带来的预期回报(即Q值)。机器人的任务是在每一步选择那个预期回报最高的动作。这就好比不是告诉机器人具体怎么走,而是给每一步一个分数,让它自己找出得分最高的步骤。这种方法在离散动作空间中表现得非常好,因为可以轻松比较和选择有限个动作中的最佳选项。
现在,如果动作空间变得非常大或者是连续的(想象让机器人学习怎样以任意速度和方向跑步),基于值的方法就变得复杂且效率不高了。因为对于每一个可能的动作,你都需要计算一个预期回报,并从中选择最佳的。但在连续动作空间中,可能的动作是无限的,这使得找出最佳动作变得非常困难。
相反,基于策略的方法则可以更自然地处理这种情况。因为你不需要为每个可能的动作分别计算一个值,而是直接根据当前状态生成动作的概率分布。这使得机器人能够在连续的动作空间中平滑地选择动作,而不是在有限的选项中做出选择。
策略梯度优化
- 基于策略的强化学习直接对策略本身进行优化,而不是像在DQN中那样间接通过Q值来推导策略。
- 策略本身通常由一个神经网络表示,输入是状态,输出是在这个状态下采取每个可能动作的概率。
- 策略梯度方法是通过调整策略网络的参数来直接最大化累积回报的期望值。
- 其中,REINFORCE 算法是一种经典的策略梯度方法。
- 在REINFORCE中,我们让策略网络指导动作的选择,然后根据实际获得的回报来调整网络参数。
- 简短说,如果一个动作导致了正的回报,那么我们就增加未来选择这个动作的概率;反之,如果导致了负面的回报,那么选择这个动作的概率就会减少。
- 具体的算法步骤如下:
- 初始化策略模型:策略通常由一个参数化的模型表示,比如一个神经网络。这个网络根据输入的状态来输出每个可行动作的概率。
- 生成一个或多个片段:在每个迭代中,使用当前的策略在环境中执行多个完整的轨迹(Trajectory),直到达到终止状态。每个轨迹是一个状态、动作和回报的序列。
- 计算回报:对于轨迹中的每个步骤,计算从当前状态到轨迹结束所获得的累积回报。这个累积回报通常是对未来回报的一个折扣累计和,其中折扣因子 γ 决定了未来回报的权重。
- 策略梯度更新:对于轨迹中的每个步骤,调整策略模型的参数,以增加在给定状态下选择实际执行的动作的概率。这个调整是根据策略梯度进行的,通常使用梯度上升法来实现。策略梯度由每个步骤的累积回报和动作概率的梯度的乘积给出。 重复上述步骤直到策略收敛或达到某个性能标准。
策略梯度的基本形式可以表示为:
$$
\nabla_\theta J(\theta)=\mathbb{E}\left[\sum_{t=0}^T G_t \cdot \nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right)\right]
$$
从直观上我们可以这些解释上述公式:
- 期望回报: $J(\theta)$ 是在策略 $\pi_\theta$ 下的期望回报。我们的目标是调整 $\theta$ 来最大化 $J(\theta)$ 。
- 梯度上升: 由于我们要最大化 $J(\theta)$ ,我们需要朝着梯度 $\nabla_\theta J(\theta)$ 的方向调整 $\theta$ 。这意味着如果某个方向上的梯度为正,增加 $\theta$ 在这个方向上的值会增加期望回报。
- 策略概率的对数: $\log \pi_\theta\left(a_t \mid s_t\right)$ 是在给定状态 $s_t$ 下选择动作 $a_t$ 的策略概率的自然对数。对数运算使得梯度计算更为稳定和高效。
- 梯度 $\nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right)$ : 这部分表明策略概率对参数 $\theta$ 的敏感程度。直观上说,它告诉我们,微小地调整 $\theta$会如何影响在状态 $s_t$ 下选择动作 $a_t$ 的概率。
- 累积回报 $G_t$ : 这是从时间 $t$ 到轨迹结束的累积折扣回报。 $G_t$ 的引入确保了动作的选择不仅考虑立即回报,而是基于其长期影响。通过 $G_t$ ,策略梯度方法可以促进那些可能立即回报不高,但长期效果好的动作。
- 期望: 外层的期望 $\mathbb{E}$ 表示这个梯度是在所有可能轨迹下的平均梯度。由于直接计算整个期望通常不可行,实践中常常通过从当前策略中采样一个或多个轨迹来估计这个期望。
 为什么要将策略概率对数的梯度与累积回报相乘?
为什么要将策略概率对数的梯度与累积回报相乘?
 示例代码:基于策略的强化学习
示例代码:基于策略的强化学习
- 定义策略网络
策略网络输出层使用softmax激活函数生成动作概率分布。
# 定义策略网络类
class PolicyNetwork(nn.Module):
def __init__(self, n_states, n_actions):
super(PolicyNetwork, self).__init__()
self.fc1 = nn.Linear(n_states, 128)
self.fc2 = nn.Linear(128, n_actions)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.softmax(self.fc2(x), dim=-1) # 使用softmax激活函数
return x
- 策略梯度算法
实现策略梯度算法(如REINFORCE)更新策略网络。
# 定义策略梯度强化学习算法类
class PolicyGradient:
def __init__(self, model, memory, cfg):
self.n_actions = cfg['n_actions']
self.device = torch.device(cfg['device'])
self.gamma = cfg['gamma']
self.policy_net = model.to(self.device)
self.optimizer = optim.Adam(self.policy_net.parameters(), lr=cfg['lr'])
self.memory = memory
# 采样动作方法
def sample_action(self, state):
state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
probs = self.policy_net(state).cpu().detach().numpy().flatten()
action = np.random.choice(self.n_actions, p=probs)
return action
# 更新策略网络
def update(self):
if len(self.memory) < self.memory.capacity:
return
state_batch, action_batch, reward_batch, _, _ = self.memory.sample(self.memory.capacity)
state_batch = torch.tensor(np.array(state_batch), device=self.device, dtype=torch.float32)
action_batch = torch.tensor(action_batch, device=self.device)
reward_batch = torch.tensor(reward_batch, device=self.device, dtype=torch.float32)
# 计算每个时间步的折扣回报
G = np.zeros_like(reward_batch)
for t in range(len(reward_batch)):
G_sum = 0
discount = 1
for k in range(t, len(reward_batch)):
G_sum += reward_batch[k] * discount
discount *= self.gamma
G[t] = G_sum
G = torch.tensor(G, dtype=torch.float32, device=self.device)
self.optimizer.zero_grad()
state_action_values = self.policy_net(state_batch)
log_probs = torch.log(state_action_values.gather(1, action_batch.unsqueeze(1)))
loss = -torch.sum(log_probs * G)
loss.backward()
self.optimizer.step()- 环境和智能体配置
初始化策略梯度方法的环境和智能体。
# 环境和智能体配置函数
def env_agent_config(cfg):
env = gym.make(cfg['env_name'])
n_states = env.observation_space.shape[0]
n_actions = env.action_space.n
memory = ReplayBuffer(cfg['memory_capacity'])
agent = PolicyGradient(PolicyNetwork(n_states, n_actions), memory, cfg)
return env, agent
- 训练和测试
# 训练函数
def train(cfg, env, agent):
print("开始训练!")
rewards = []
steps = []
for i_ep in range(cfg['train_eps']):
ep_reward = 0
ep_step = 0
state, _ = env.reset()
done = False
while not done:
ep_step += 1
action = agent.sample_action(state)
next_state, reward, done, truncated, _ = env.step(action)
done = done or truncated
agent.memory.push((state, action, reward, next_state, done))
state = next_state
ep_reward += reward
if done:
break
agent.update()
steps.append(ep_step)
rewards.append(ep_reward)
if (i_ep + 1) % 10 == 0:
print(f"回合:{i_ep + 1}/{cfg['train_eps']},奖励:{ep_reward:.2f}")
print("完成训练!")
env.close()
return {'rewards': rewards}
# 测试函数
def test(cfg, env, agent):
print("开始测试!")
rewards = []
steps = []
for i_ep in range(cfg['test_eps']):
ep_reward = 0
ep_step = 0
state, _ = env.reset()
done = False
while not done and ep_step < cfg['ep_max_steps']:
ep_step += 1
action = agent.sample_action(state)
next_state, reward, done, truncated, _ = env.step(action)
done = done or truncated
state = next_state
ep_reward += reward
if done:
print(f"回合 {i_ep + 1} 在步数 {ep_step} 完成")
steps.append(ep_step)
rewards.append(ep_reward)
print(f"回合:{i_ep + 1}/{cfg['test_eps']},奖励:{ep_reward:.2f}")
print("完成测试")
env.close()
return {'rewards': rewards}
# 获取配置参数函数
def get_args():
return {
'env_name': 'CartPole-v1',
'n_actions': 2,
'device': 'cpu',
'gamma': 0.99,
'epsilon_start': 1.0,
'epsilon_end': 0.01,
'epsilon_decay': 500,
'batch_size': 64,
'lr': 0.001,
'memory_capacity': 10000,
'train_eps': 100,
'test_eps': 100,
'ep_max_steps': 200,
'target_update': 10,
'seed': 42
}
# 绘制奖励曲线函数
def plot_rewards(rewards, cfg, tag="train"):
import matplotlib.pyplot as plt
plt.plot(rewards)
plt.title(f'{tag} Rewards')
plt.show()
# 获取参数
cfg = get_args()
# 训练
env, agent = env_agent_config(cfg)
res_dic = train(cfg, env, agent)
# 绘制训练奖励曲线
plot_rewards(res_dic['rewards'], cfg, tag="train")
# 测试
res_dic = test(cfg, env, agent)
# 绘制测试奖励曲线
plot_rewards(res_dic['rewards'], cfg, tag="test")
开始训练!
回合:10/100,奖励:46.00
回合:20/100,奖励:11.00
回合:30/100,奖励:33.00
回合:40/100,奖励:16.00
回合:50/100,奖励:16.00
回合:60/100,奖励:11.00
回合:70/100,奖励:24.00
回合:80/100,奖励:12.00
回合:90/100,奖励:20.00
回合:100/100,奖励:60.00
完成训练!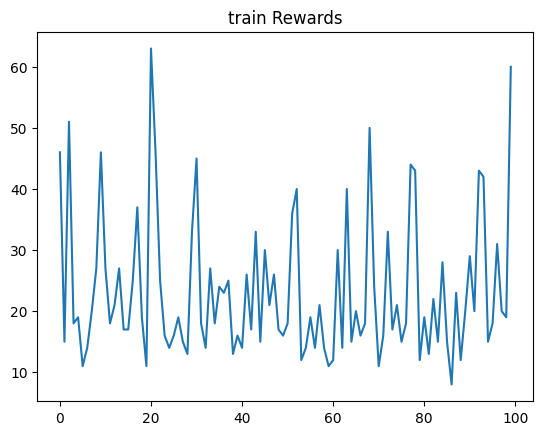
开始测试!
回合 1 在步数 18 完成
回合:1/100,奖励:18.00
回合 2 在步数 15 完成
回合:2/100,奖励:15.00
回合 3 在步数 22 完成
回合:3/100,奖励:22.00
回合 4 在步数 25 完成
回合:4/100,奖励:25.00
回合 5 在步数 21 完成
回合:5/100,奖励:21.00
回合 6 在步数 33 完成
回合:6/100,奖励:33.00
回合 7 在步数 20 完成
回合:7/100,奖励:20.00
回合 8 在步数 22 完成
回合:8/100,奖励:22.00
回合 9 在步数 30 完成
回合:9/100,奖励:30.00
回合 10 在步数 18 完成
回合:10/100,奖励:18.00
回合 11 在步数 16 完成
回合:11/100,奖励:16.00
回合 12 在步数 20 完成
回合:12/100,奖励:20.00
回合 13 在步数 16 完成
回合:13/100,奖励:16.00
回合 14 在步数 27 完成
回合:14/100,奖励:27.00
回合 15 在步数 13 完成
回合:15/100,奖励:13.00
回合 16 在步数 26 完成
回合:16/100,奖励:26.00
回合 17 在步数 24 完成
回合:17/100,奖励:24.00
回合 18 在步数 15 完成
回合:18/100,奖励:15.00
回合 19 在步数 12 完成
回合:19/100,奖励:12.00
回合 20 在步数 22 完成
回合:20/100,奖励:22.00
回合 21 在步数 52 完成
回合:21/100,奖励:52.00
回合 22 在步数 18 完成
回合:22/100,奖励:18.00
回合 23 在步数 35 完成
回合:23/100,奖励:35.00
回合 24 在步数 47 完成
回合:24/100,奖励:47.00
回合 25 在步数 9 完成
回合:25/100,奖励:9.00
回合 26 在步数 32 完成
回合:26/100,奖励:32.00
回合 27 在步数 12 完成
回合:27/100,奖励:12.00
回合 28 在步数 14 完成
回合:28/100,奖励:14.00
回合 29 在步数 46 完成
回合:29/100,奖励:46.00
回合 30 在步数 55 完成
回合:30/100,奖励:55.00
回合 31 在步数 21 完成
回合:31/100,奖励:21.00
回合 32 在步数 12 完成
回合:32/100,奖励:12.00
回合 33 在步数 9 完成
回合:33/100,奖励:9.00
回合 34 在步数 26 完成
回合:34/100,奖励:26.00
回合 35 在步数 26 完成
回合:35/100,奖励:26.00
回合 36 在步数 20 完成
回合:36/100,奖励:20.00
回合 37 在步数 25 完成
回合:37/100,奖励:25.00
回合 38 在步数 34 完成
回合:38/100,奖励:34.00
回合 39 在步数 13 完成
回合:39/100,奖励:13.00
回合 40 在步数 23 完成
回合:40/100,奖励:23.00
回合 41 在步数 23 完成
回合:41/100,奖励:23.00
回合 42 在步数 30 完成
回合:42/100,奖励:30.00
回合 43 在步数 16 完成
回合:43/100,奖励:16.00
回合 44 在步数 50 完成
回合:44/100,奖励:50.00
回合 45 在步数 13 完成
回合:45/100,奖励:13.00
回合 46 在步数 15 完成
回合:46/100,奖励:15.00
回合 47 在步数 44 完成
回合:47/100,奖励:44.00
回合 48 在步数 11 完成
回合:48/100,奖励:11.00
回合 49 在步数 51 完成
回合:49/100,奖励:51.00
回合 50 在步数 18 完成
回合:50/100,奖励:18.00
回合 51 在步数 11 完成
回合:51/100,奖励:11.00
回合 52 在步数 11 完成
回合:52/100,奖励:11.00
回合 53 在步数 33 完成
回合:53/100,奖励:33.00
回合 54 在步数 19 完成
回合:54/100,奖励:19.00
回合 55 在步数 19 完成
回合:55/100,奖励:19.00
回合 56 在步数 17 完成
回合:56/100,奖励:17.00
回合 57 在步数 10 完成
回合:57/100,奖励:10.00
回合 58 在步数 22 完成
回合:58/100,奖励:22.00
回合 59 在步数 25 完成
回合:59/100,奖励:25.00
回合 60 在步数 28 完成
回合:60/100,奖励:28.00
回合 61 在步数 30 完成
回合:61/100,奖励:30.00
回合 62 在步数 18 完成
回合:62/100,奖励:18.00
回合 63 在步数 54 完成
回合:63/100,奖励:54.00
回合 64 在步数 35 完成
回合:64/100,奖励:35.00
回合 65 在步数 57 完成
回合:65/100,奖励:57.00
回合 66 在步数 27 完成
回合:66/100,奖励:27.00
回合 67 在步数 10 完成
回合:67/100,奖励:10.00
回合 68 在步数 28 完成
回合:68/100,奖励:28.00
回合 69 在步数 31 完成
回合:69/100,奖励:31.00
回合 70 在步数 18 完成
回合:70/100,奖励:18.00
回合 71 在步数 8 完成
回合:71/100,奖励:8.00
回合 72 在步数 16 完成
回合:72/100,奖励:16.00
回合 73 在步数 29 完成
回合:73/100,奖励:29.00
回合 74 在步数 12 完成
回合:74/100,奖励:12.00
回合 75 在步数 38 完成
回合:75/100,奖励:38.00
回合 76 在步数 31 完成
回合:76/100,奖励:31.00
回合 77 在步数 17 完成
回合:77/100,奖励:17.00
回合 78 在步数 29 完成
回合:78/100,奖励:29.00
回合 79 在步数 68 完成
回合:79/100,奖励:68.00
回合 80 在步数 16 完成
回合:80/100,奖励:16.00
回合 81 在步数 24 完成
回合:81/100,奖励:24.00
回合 82 在步数 13 完成
回合:82/100,奖励:13.00
回合 83 在步数 22 完成
回合:83/100,奖励:22.00
回合 84 在步数 11 完成
回合:84/100,奖励:11.00
回合 85 在步数 21 完成
回合:85/100,奖励:21.00
回合 86 在步数 22 完成
回合:86/100,奖励:22.00
回合 87 在步数 16 完成
回合:87/100,奖励:16.00
回合 88 在步数 13 完成
回合:88/100,奖励:13.00
回合 89 在步数 15 完成
回合:89/100,奖励:15.00
回合 90 在步数 14 完成
回合:90/100,奖励:14.00
回合 91 在步数 21 完成
回合:91/100,奖励:21.00
回合 92 在步数 15 完成
回合:92/100,奖励:15.00
回合 93 在步数 24 完成
回合:93/100,奖励:24.00
回合 94 在步数 14 完成
回合:94/100,奖励:14.00
回合 95 在步数 28 完成
回合:95/100,奖励:28.00
回合 96 在步数 56 完成
回合:96/100,奖励:56.00
回合 97 在步数 51 完成
回合:97/100,奖励:51.00
回合 98 在步数 15 完成
回合:98/100,奖励:15.00
回合 99 在步数 22 完成
回合:99/100,奖励:22.00
回合 100 在步数 26 完成
回合:100/100,奖励:26.00
完成测试
 演员评论家模型(Actor-Critic model)
演员评论家模型(Actor-Critic model)
演员-评论家(Actor-Critic)模型是一种结合了基于值的方法和基于策略的方法的强化学习框架。 这个模型的核心思想是将策略决策(演员)和值函数估计(评论家)的优点结合起来,以期达到更好的学习效率和策略性能。
演员部分负责基于当前策略选择动作。
- 这个策略通常是随机的,允许算法在探索(尝试新动作)和利用(选择已知最佳动作)之间取得平衡。演员的策略是通过某种参数化形式实现的,一般使用神经网络,其参数通过策略梯度方法更新。具体解释如下:
- 输入: 演员网络的输入通常是环境的当前状态。
- 输出: 输出是对每个可能动作的概率分布 (在离散动作空间中) 或者特定动作的参数 (如均值和标准差,在连续动作空间中)。
- 损失函数: 演员网络的训练通常通过策略梯度方法,例如REINFORCE或Actor-Critic方法的策略梯度。
- 优化方法: 梯度上升是常用的优化方法,用于最大化奖励期望。
评论家部分估计所选动作的价值
- 通常是状态-动作对的Q值或仅是状态的价值V。这个评价帮助演员判断所选择的动作是好是坏。评论家的更新通常依赖于TD-Learning或其他值函数近似方法,并且它提供的价值反馈用于指导演员的策略更新。具体解释如下:
- 输入: 输入通常是当前状态或状态和动作的组合。
- 输出: 输出是对当前状态或状态-动作对的价值估计,即 Q 值 (状态-动作值函数) 或 V 值 (状态值函数)。
- 损失函数: 评论家的损失函数通常是TD误差的平方。
- 优化方法: 梯度下降是最常用的优化方法,用于最小化价值估计的误差。
在演员-评论家(Actor-Critic)模型中,学习过程涉及到一个交互式的环节。
- 演员负责选择动作
- 评论家则评估这些动作的好坏。
- 下面详细解释这个过程的每个步骤:
- Step1:基于当前策略,演员选择一个动作。
- Step2:环境反馈,环境根据选择的动作返回新的状态和奖励。
- Step3:学习更新,评论家使用TD误差来评估所采取动作的价值。 同时,演员根据评论家的反馈来更新其策略,以增加在类似情境下选择更有价值动作的概率。
- Step4:迭代下去直到轨迹结束
演员-评论家模型算法的优缺点
- 优点如下:
1.稳定性与效率的结合: 演员-评论家模型结合了基于策略的方法(如REINFORCE)的优点和基于值的方法(如Q学习或DQN)的优点,比单独使用策略梯度方法或值函数方法更稳定和高效。
2.适用于连续动作空间: 与仅基于值的方法(如DQN)不同,演员-评论家模型适用于连续动作空间的问题,使其在处理诸如机器人控制等问题时更为有效。这个优点是继承自基于策略的强化学习的。
3.减少方差,提高学习效率: 评论家的引入帮助减少策略估计的方差,从而提高学习的效率。这个优点是继承自基于价值的强化学习的。
4.在线学习和离线学习: 可以应用于在线学习(从每个步骤中学习)和离线学习(从一个完整的情节中学习),提供灵活的学习方式。
- 缺点如下:
- 复杂性和计算成本: 需要同时训练两个模型(演员和评论家),这可能导致模型更加复杂和计算成本更高。
- 稳定性问题: 尽管比纯策略梯度方法更稳定,但是演员-评论家算法的稳定性仍然不如传统的基于值的方法,如DQN。
- 调参难度: 需要调整更多的超参数(如两个不同网络的学习率、折扣因子等),调参可能比单一模型方法更加困难。
- 过度估计的风险: 由于评论家模型可能过度估计值函数,特别是在使用函数逼近器(如神经网络)时,可能导致学习过程不稳定。
 示例代码:演员评论家模型
示例代码:演员评论家模型
class ActorCriticNetwork(nn.Module):
def __init__(self, n_states, n_actions):
super(ActorCriticNetwork, self).__init__()
self.fc1 = nn.Linear(n_states, 256)
self.fc2 = nn.Linear(256, 128)
self.actor = nn.Linear(128, n_actions)
self.critic = nn.Linear(128, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
policy_dist = F.softmax(self.actor(x), dim=-1)
value = self.critic(x)
return policy_dist, value
class ActorCritic:
def __init__(self, model, memory, cfg):
self.n_actions = cfg['n_actions']
self.device = torch.device(cfg['device'])
self.gamma = cfg['gamma']
self.model = model.to(self.device)
self.optimizer = optim.Adam(self.model.parameters(), lr=cfg['lr'])
self.memory = memory
# 采样动作方法
def sample_action(self, state):
state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0) # 将状态转换为张量
policy_dist, _ = self.model(state) # 获取策略分布
policy_dist = policy_dist.cpu().detach().numpy().flatten() # 将策略分布转换为numpy数组并展平
action = np.random.choice(self.n_actions, p=policy_dist) # 根据策略分布采样动作
return action
# 更新模型方法
def update(self):
if len(self.memory) < self.memory.capacity: # 如果缓冲区中的经验不足
return
# 从缓冲区采样一个批次的经验
state_batch, action_batch, reward_batch, next_state_batch, done_batch = self.memory.sample(self.memory.capacity)
state_batch = torch.tensor(np.array(state_batch), device=self.device, dtype=torch.float32) # 将状态转换为张量
action_batch = torch.tensor(action_batch, device=self.device) # 将动作转换为张量
reward_batch = torch.tensor(reward_batch, device=self.device, dtype=torch.float32) # 将奖励转换为张量
next_state_batch = torch.tensor(np.array(next_state_batch), device=self.device, dtype=torch.float32) # 将下一个状态转换为张量
done_batch = torch.tensor(done_batch, device=self.device, dtype=torch.float32) # 将完成标志转换为张量
# 获取下一个状态的价值
_, next_value = self.model(next_state_batch)
# 计算目标价值
target_values = reward_batch + self.gamma * next_value.squeeze() * (1 - done_batch)
# 获取当前状态的策略分布和价值
policy_dist, values = self.model(state_batch)
values = values.squeeze() # 去掉多余的维度
# 计算优势
advantages = target_values - values
# 计算策略的对数概率
log_probs = torch.log(policy_dist.gather(1, action_batch.unsqueeze(1)))
actor_loss = -torch.sum(log_probs.squeeze() * advantages.detach()) # 策略损失
critic_loss = F.mse_loss(values, target_values.detach()) # 价值损失
loss = actor_loss + critic_loss # 总损失
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
def env_agent_config(cfg):
env = gym.make(cfg['env_name'])
n_states = env.observation_space.shape[0]
n_actions = env.action_space.n
memory = ReplayBuffer(cfg['memory_capacity'])
agent = ActorCritic(ActorCriticNetwork(n_states, n_actions), memory, cfg)
return env, agent
def train(cfg, env, agent):
print("开始训练!")
rewards = []
steps = []
for i_ep in range(cfg['train_eps']):
ep_reward = 0
ep_step = 0
state, _ = env.reset()
done = False
while not done:
ep_step += 1
action = agent.sample_action(state)
next_state, reward, done, truncated, _ = env.step(action)
done = done or truncated
agent.memory.push((state, action, reward, next_state, done))
state = next_state
ep_reward += reward
if done:
break
agent.update()
steps.append(ep_step)
rewards.append(ep_reward)
if (i_ep + 1) % 10 == 0:
print(f"回合:{i_ep + 1}/{cfg['train_eps']},奖励:{ep_reward:.2f}")
print("完成训练!")
env.close()
return {'rewards': rewards}
def test(cfg, env, agent):
print("开始测试!")
rewards = []
steps = []
for i_ep in range(cfg['test_eps']):
ep_reward = 0
ep_step = 0
state, _ = env.reset()
done = False
while not done and ep_step < cfg['ep_max_steps']:
ep_step += 1
action = agent.sample_action(state)
next_state, reward, done, truncated, _ = env.step(action)
done = done or truncated
state = next_state
ep_reward += reward
if done:
print(f"回合 {i_ep + 1} 在步数 {ep_step} 完成")
steps.append(ep_step)
rewards.append(ep_reward)
print(f"回合:{i_ep + 1}/{cfg['test_eps']},奖励:{ep_reward:.2f}")
print("完成测试")
env.close()
return {'rewards': rewards}
def get_args():
return {
'env_name': 'CartPole-v1',
'n_actions': 2,
'device': 'cpu',
'gamma': 0.99, # 调整折扣因子
'lr': 0.0005, # 调整学习率
'memory_capacity': 10000,
'train_eps': 100, # 增加训练回合数
'test_eps': 100,
'ep_max_steps': 200,
'seed': 42
}
def plot_rewards(rewards, cfg, tag="train"):
import matplotlib.pyplot as plt
plt.plot(rewards)
plt.title(f'{tag} Rewards')
plt.show()
cfg = get_args()
env, agent = env_agent_config(cfg)
res_dic = train(cfg, env, agent)
plot_rewards(res_dic['rewards'], cfg, tag="train")
res_dic = test(cfg, env, agent)
plot_rewards(res_dic['rewards'], cfg, tag="test")
开始训练!
回合:10/100,奖励:19.00
回合:20/100,奖励:10.00
回合:30/100,奖励:11.00
回合:40/100,奖励:11.00
回合:50/100,奖励:36.00
回合:60/100,奖励:34.00
回合:70/100,奖励:28.00
回合:80/100,奖励:81.00
回合:90/100,奖励:25.00
回合:100/100,奖励:26.00
完成训练!
开始测试!
回合 1 在步数 19 完成
回合:1/100,奖励:19.00
回合 2 在步数 13 完成
回合:2/100,奖励:13.00
回合 3 在步数 16 完成
回合:3/100,奖励:16.00
回合 4 在步数 11 完成
回合:4/100,奖励:11.00
回合 5 在步数 10 完成
回合:5/100,奖励:10.00
回合 6 在步数 19 完成
回合:6/100,奖励:19.00
回合 7 在步数 10 完成
回合:7/100,奖励:10.00
回合 8 在步数 43 完成
回合:8/100,奖励:43.00
回合 9 在步数 18 完成
回合:9/100,奖励:18.00
回合 10 在步数 17 完成
回合:10/100,奖励:17.00
回合 11 在步数 11 完成
回合:11/100,奖励:11.00
回合 12 在步数 15 完成
回合:12/100,奖励:15.00
回合 13 在步数 22 完成
回合:13/100,奖励:22.00
回合 14 在步数 21 完成
回合:14/100,奖励:21.00
回合 15 在步数 13 完成
回合:15/100,奖励:13.00
回合 16 在步数 9 完成
回合:16/100,奖励:9.00
回合 17 在步数 8 完成
回合:17/100,奖励:8.00
回合 18 在步数 17 完成
回合:18/100,奖励:17.00
回合 19 在步数 44 完成
回合:19/100,奖励:44.00
回合 20 在步数 12 完成
回合:20/100,奖励:12.00
回合 21 在步数 30 完成
回合:21/100,奖励:30.00
回合 22 在步数 19 完成
回合:22/100,奖励:19.00
回合 23 在步数 21 完成
回合:23/100,奖励:21.00
回合 24 在步数 28 完成
回合:24/100,奖励:28.00
回合 25 在步数 14 完成
回合:25/100,奖励:14.00
回合 26 在步数 9 完成
回合:26/100,奖励:9.00
回合 27 在步数 25 完成
回合:27/100,奖励:25.00
回合 28 在步数 26 完成
回合:28/100,奖励:26.00
回合 29 在步数 20 完成
回合:29/100,奖励:20.00
回合 30 在步数 12 完成
回合:30/100,奖励:12.00
回合 31 在步数 22 完成
回合:31/100,奖励:22.00
回合 32 在步数 22 完成
回合:32/100,奖励:22.00
回合 33 在步数 26 完成
回合:33/100,奖励:26.00
回合 34 在步数 21 完成
回合:34/100,奖励:21.00
回合 35 在步数 17 完成
回合:35/100,奖励:17.00
回合 36 在步数 22 完成
回合:36/100,奖励:22.00
回合 37 在步数 12 完成
回合:37/100,奖励:12.00
回合 38 在步数 25 完成
回合:38/100,奖励:25.00
回合 39 在步数 10 完成
回合:39/100,奖励:10.00
回合 40 在步数 15 完成
回合:40/100,奖励:15.00
回合 41 在步数 10 完成
回合:41/100,奖励:10.00
回合 42 在步数 9 完成
回合:42/100,奖励:9.00
回合 43 在步数 22 完成
回合:43/100,奖励:22.00
回合 44 在步数 15 完成
回合:44/100,奖励:15.00
回合 45 在步数 15 完成
回合:45/100,奖励:15.00
回合 46 在步数 12 完成
回合:46/100,奖励:12.00
回合 47 在步数 29 完成
回合:47/100,奖励:29.00
回合 48 在步数 14 完成
回合:48/100,奖励:14.00
回合 49 在步数 16 完成
回合:49/100,奖励:16.00
回合 50 在步数 18 完成
回合:50/100,奖励:18.00
回合 51 在步数 18 完成
回合:51/100,奖励:18.00
回合 52 在步数 18 完成
回合:52/100,奖励:18.00
回合 53 在步数 12 完成
回合:53/100,奖励:12.00
回合 54 在步数 15 完成
回合:54/100,奖励:15.00
回合 55 在步数 19 完成
回合:55/100,奖励:19.00
回合 56 在步数 36 完成
回合:56/100,奖励:36.00
回合 57 在步数 44 完成
回合:57/100,奖励:44.00
回合 58 在步数 21 完成
回合:58/100,奖励:21.00
回合 59 在步数 22 完成
回合:59/100,奖励:22.00
回合 60 在步数 22 完成
回合:60/100,奖励:22.00
回合 61 在步数 23 完成
回合:61/100,奖励:23.00
回合 62 在步数 53 完成
回合:62/100,奖励:53.00
回合 63 在步数 10 完成
回合:63/100,奖励:10.00
回合 64 在步数 26 完成
回合:64/100,奖励:26.00
回合 65 在步数 20 完成
回合:65/100,奖励:20.00
回合 66 在步数 26 完成
回合:66/100,奖励:26.00
回合 67 在步数 13 完成
回合:67/100,奖励:13.00
回合 68 在步数 11 完成
回合:68/100,奖励:11.00
回合 69 在步数 19 完成
回合:69/100,奖励:19.00
回合 70 在步数 20 完成
回合:70/100,奖励:20.00
回合 71 在步数 11 完成
回合:71/100,奖励:11.00
回合 72 在步数 31 完成
回合:72/100,奖励:31.00
回合 73 在步数 25 完成
回合:73/100,奖励:25.00
回合 74 在步数 34 完成
回合:74/100,奖励:34.00
回合 75 在步数 13 完成
回合:75/100,奖励:13.00
回合 76 在步数 21 完成
回合:76/100,奖励:21.00
回合 77 在步数 9 完成
回合:77/100,奖励:9.00
回合 78 在步数 16 完成
回合:78/100,奖励:16.00
回合 79 在步数 17 完成
回合:79/100,奖励:17.00
回合 80 在步数 42 完成
回合:80/100,奖励:42.00
回合 81 在步数 16 完成
回合:81/100,奖励:16.00
回合 82 在步数 19 完成
回合:82/100,奖励:19.00
回合 83 在步数 18 完成
回合:83/100,奖励:18.00
回合 84 在步数 23 完成
回合:84/100,奖励:23.00
回合 85 在步数 22 完成
回合:85/100,奖励:22.00
回合 86 在步数 45 完成
回合:86/100,奖励:45.00
回合 87 在步数 26 完成
回合:87/100,奖励:26.00
回合 88 在步数 87 完成
回合:88/100,奖励:87.00
回合 89 在步数 14 完成
回合:89/100,奖励:14.00
回合 90 在步数 11 完成
回合:90/100,奖励:11.00
回合 91 在步数 15 完成
回合:91/100,奖励:15.00
回合 92 在步数 12 完成
回合:92/100,奖励:12.00
回合 93 在步数 19 完成
回合:93/100,奖励:19.00
回合 94 在步数 23 完成
回合:94/100,奖励:23.00
回合 95 在步数 19 完成
回合:95/100,奖励:19.00
回合 96 在步数 14 完成
回合:96/100,奖励:14.00
回合 97 在步数 18 完成
回合:97/100,奖励:18.00
回合 98 在步数 28 完成
回合:98/100,奖励:28.00
回合 99 在步数 14 完成
回合:99/100,奖励:14.00
回合 100 在步数 24 完成
回合:100/100,奖励:24.00
完成测试
生成对抗网络 VS 演员-评论家模型算法
先简短回顾一下这两个模型。
生成对抗网络(GANs)
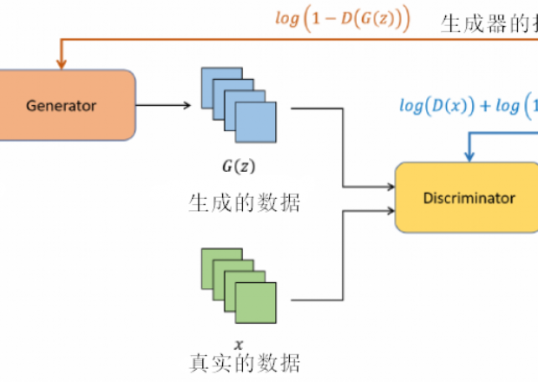
- 基本概念:GANs 由两部分组成,生成器(Generator)和判别器(Discriminator)。生成器的目标是创建逼真的数据(如图片),而判别器的目标是区分真实数据和生成器产生的假数据。
- 训练性质:在GANs中,生成器和判别器呈对抗关系。生成器尝试欺骗判别器,而判别器努力不被欺骗。这种对抗过程促进了两者的能力提升,最终生成器能产生极为逼真的数据。
- 学习机制:GANs 的学习过程是一个动态平衡的游戏,其中生成器不断改进其生成的数据以逃避判别器的识别,而判别器则不断提升其辨别能力。
演员-评论家模型
- 基本概念:演员-评论家模型由两部分组成,演员(Actor)和评论家(Critic)。演员负责选择动作,而评论家评价这些动作并提供反馈。
- 训练性质:与GANs不同,演员-评论家模型中的演员和评论家是合作关系。评论家提供的反馈帮助演员改进其策略,以此优化动作选择过程。
- 学习机制:在演员-评论家模型中,演员的动作选择受到评论家提供的价值评估指导,评论家基于演员的表现来调整自己的价值估计。这种机制有助于同时优化策略选择和价值判断。
 Q1:为什么训练性质一个是对抗,一个是合作?
Q1:为什么训练性质一个是对抗,一个是合作?
 Q2:到底是对抗提升好一些,还是合作共赢好一些?
Q2:到底是对抗提升好一些,还是合作共赢好一些?
 Credits
Credits
- Icons made by Becris from www.flaticon.com
- Icons from Icons8.com - https://icons8.com
- Dive Into Deep Learning - Recurrent Neural Networks
- DS-GA 1008 - NYU CENTER FOR DATA SCIENCE - Deep Sequence Modeling
- Text classification with the torchtext library
- Tricks For Training Transformers - Borealis AI - P. Xu, S. Prince
- Tal Daniel
作者
arwin.yu.98@gmail.com