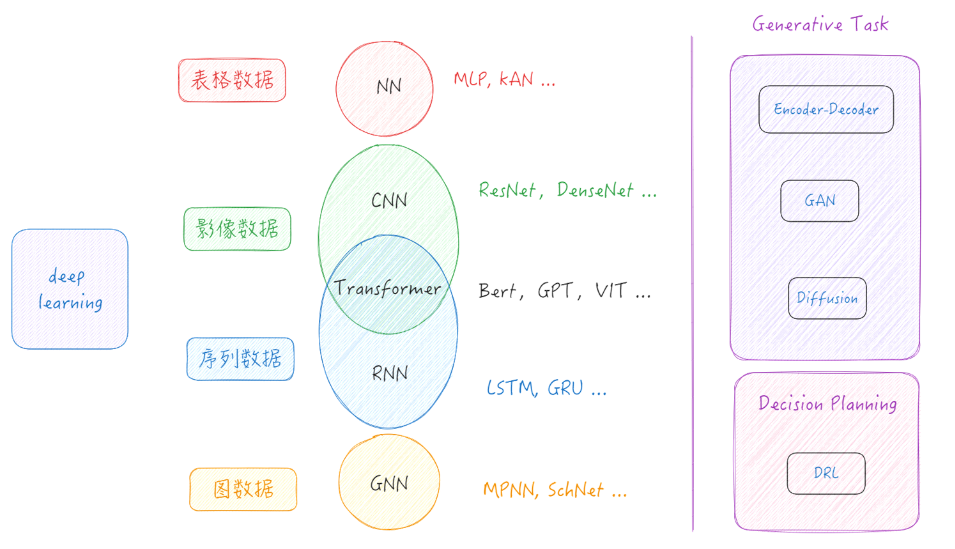
Learning Methods of Deep Learning
create by Deepfinder
Agenda
- 师徒相授：有监督学习（Supervised Learning）
- 见微知著：无监督学习（Un-supervised Learning）
- 无师自通：自监督学习（Self-supervised Learning）
- 以点带面：半监督学习（Semi-supervised learning）
- 明辨是非：对比学习（Contrastive Learning）
- 举一反三：迁移学习（Transfer Learning）
- 针锋相对：对抗学习（Adversarial Learning）
- 众志成城：集成学习(Ensemble Learning)
- 殊途同归：联邦学习（Federated Learning）
- 百折不挠：强化学习（Reinforcement Learning）
- 求知若渴：主动学习（Active Learning）
- 万法归宗：元学习（Meta-Learning）
Tutorial 01 - 师徒相授：有监督学习（Supervised Learning）
The Perceptron
-
第一个也是最简单的线性模型之一。
-
基于 线性阈值单元 (LTU)：输入和输出是数字，每个连接都与一个权重相关联。
-
LTU 计算其输入的加权和：$z = w_1x_1 + w_2x_2 +....+w_nx_n = w^Tx$，然后对该和应用 阶跃函数 并输出结果：$$ h_w(x) = step(z) = step(w^Tx) $$
-
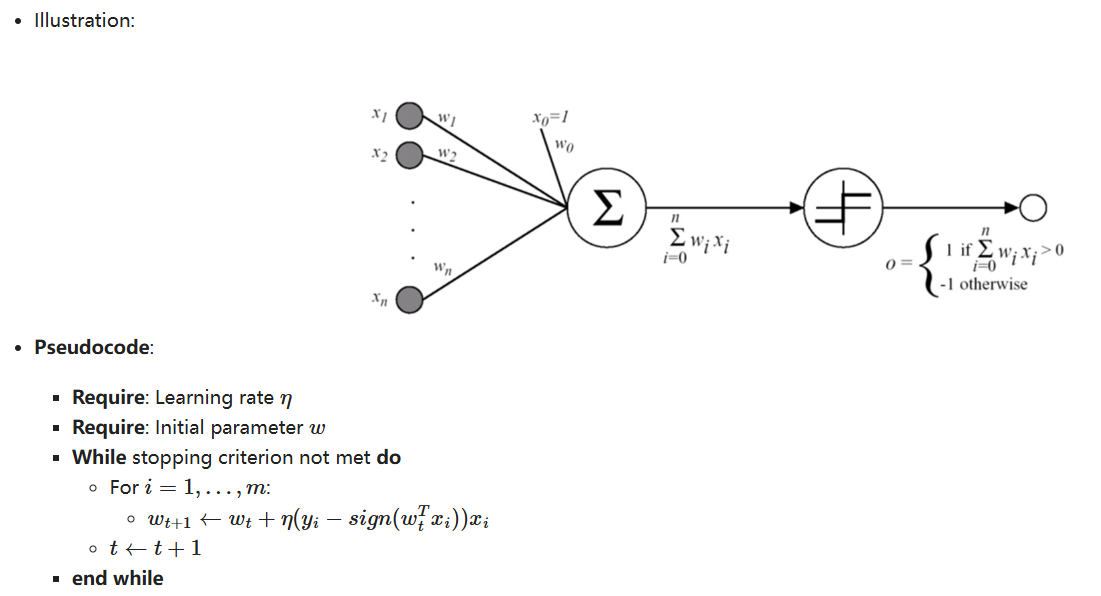
Illustration:
-
Pseudocode:
- Require: Learning rate $\eta$
- Require: Initial parameter $w$
- While stopping criterion not met do
- For $i=1,...,m$:
- $ w_{t+1} \leftarrow w_t +\eta(y_i -sign(w_t^Tx_i))x_i $
- $t \leftarrow t + 1$
- For $i=1,...,m$:
- end while
Multi-Layer Perceptron (MLP)
-
MLP 由一个输入层、一个或多个隐藏层和一个最终输出层组成。
-
当隐藏层的数量大于 2 时，网络通常称为深度神经网络 (DNN)，小于2成为MLP（一般情况下的一种习惯，不是定义）。
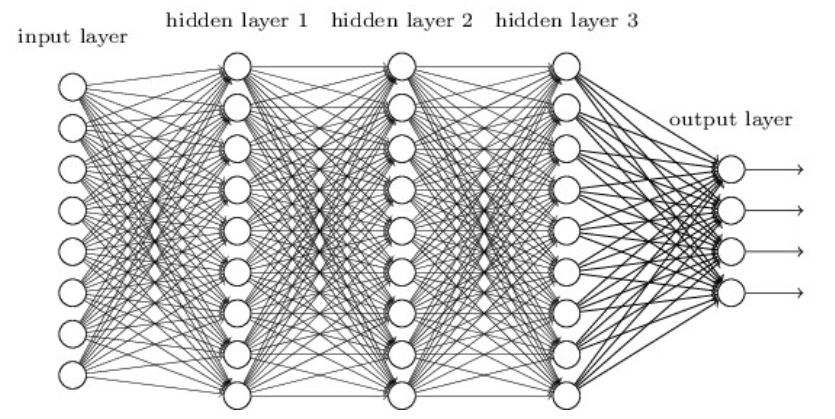
基于MLP可以衍生出各种各样的深度学习算法与模型
深度学习算法与模型的训练逻辑
Forward calculation
-
在 前向传递 中，对于每个训练实例，算法将其馈送到网络并计算每个连续层中每个神经元的输出
-
使用网络进行预测只是进行前向传递。
示例如下：
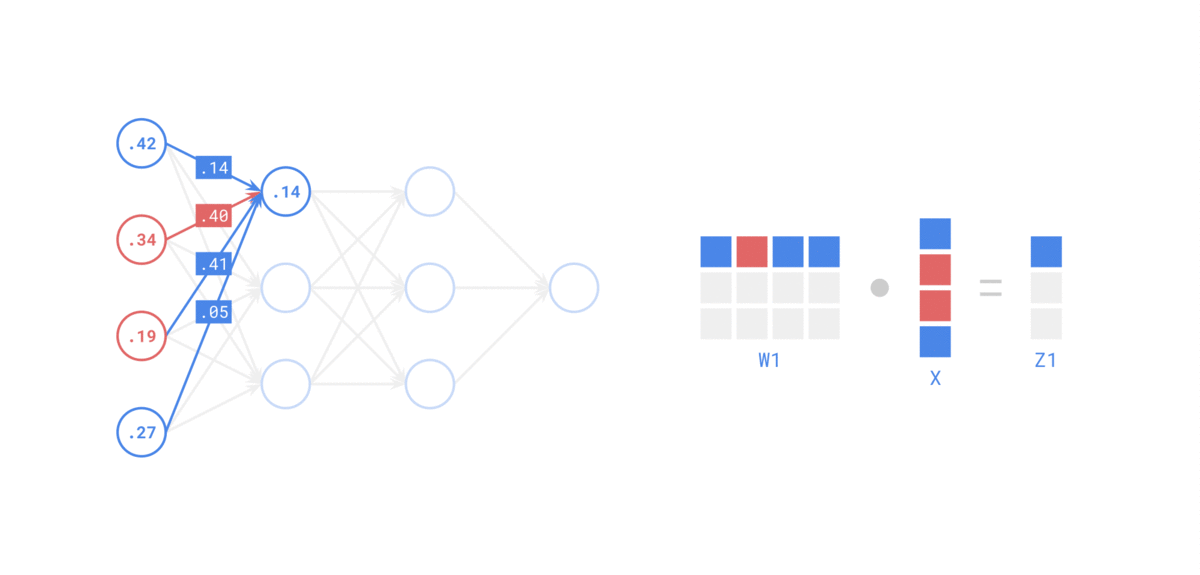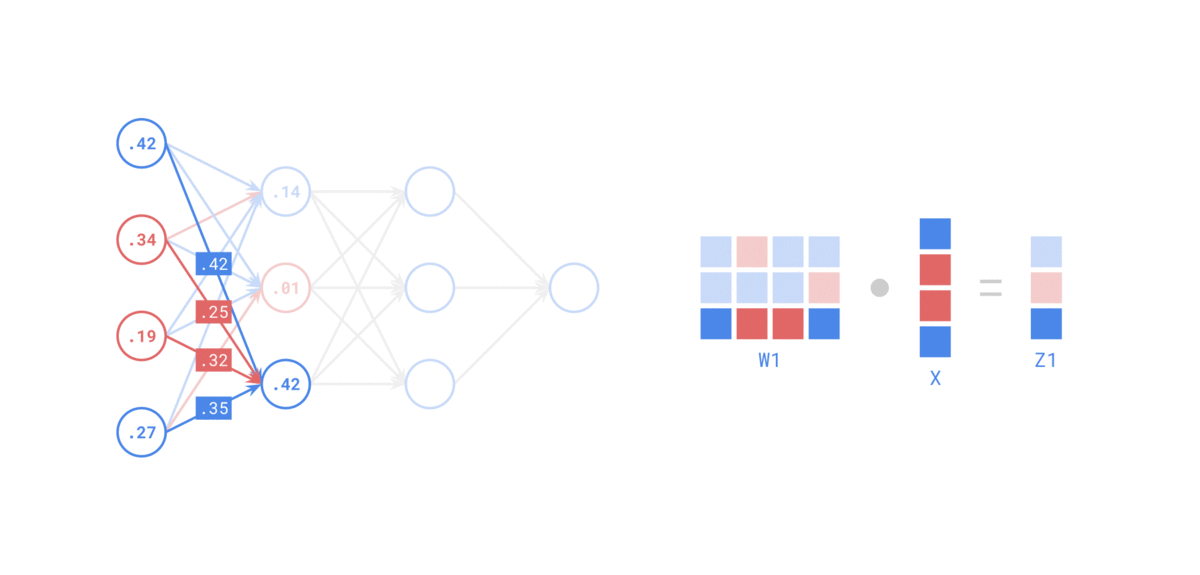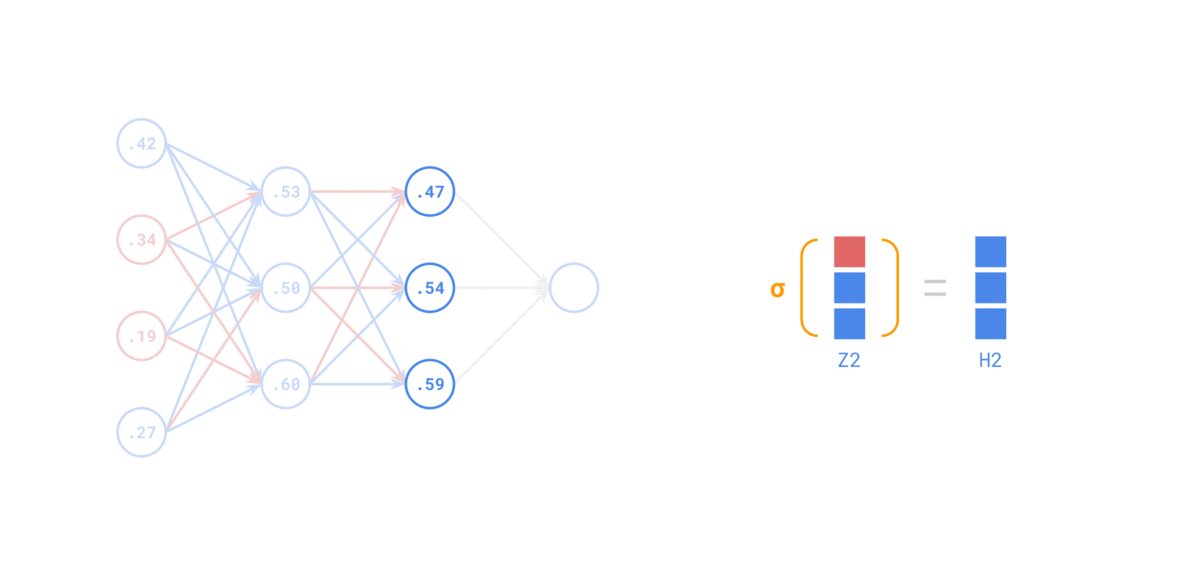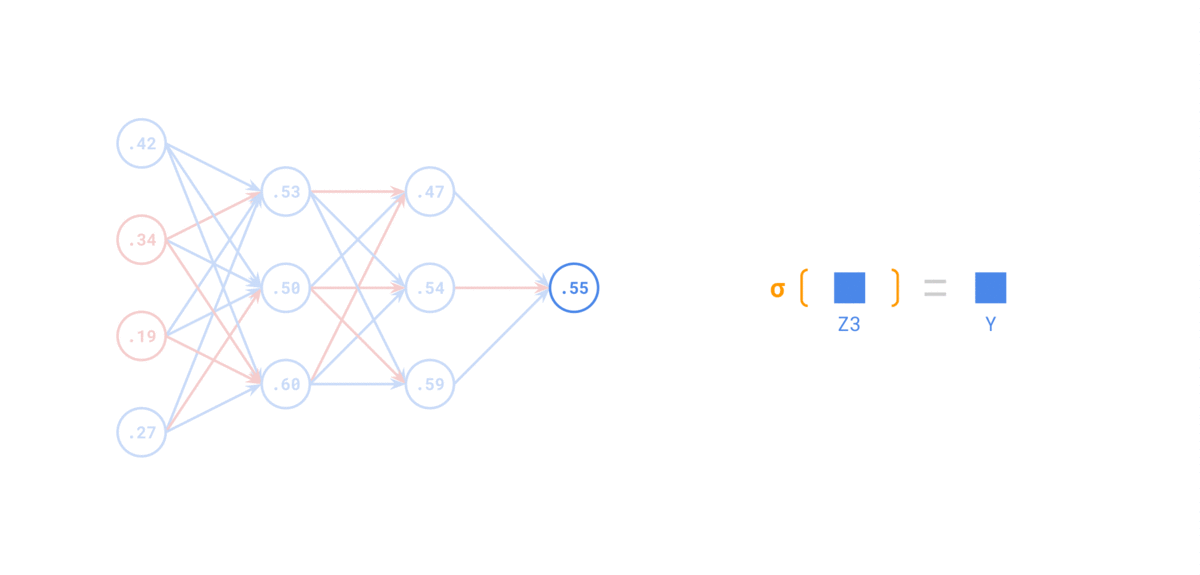
Backpropagation
反向传播是一种有效的计算梯度的方法，它可以快速计算网络中每个神经元的偏导数。反向传播通过先正向传播计算网络的输出，然后从输出层到输入层反向传播误差，最后根据误差计算每个神经元的偏导数。反向传播算法的核心思想是通过链式法则将误差向后传递，计算每个神经元对误差的贡献。
示例如下：
初始化网络，构建一个只有一层的神经网络
（1）初始化网络参数：
假设神经网络的输入和输出的初始化为: $x_1=0.5, x_2=1.0, y=0.8$ 。
参数的初始化为: $w_1=1.0, w_2=0.5, w_3=0.5, w_4=0.7, w_5=1.0, w_6=2.0$ 。
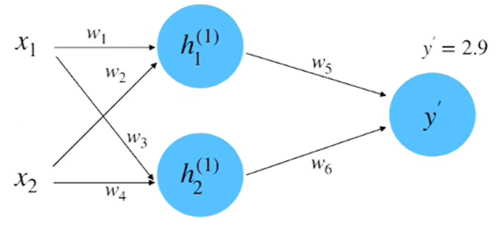
（2）前向计算, 如下图
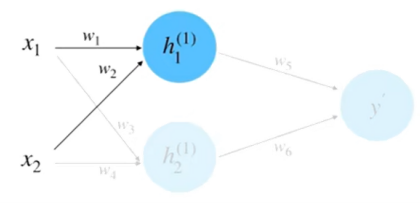
同理, 计算 $h_2$ 等于 0.95 。将 $h_1$ 和 $h_2$ 相乘求和到前向传播的计算结果, 如下图
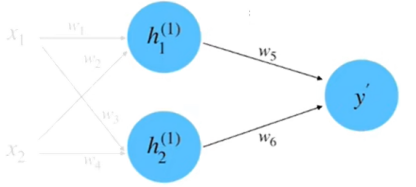
$$
\begin{aligned}
y^{\prime} & =w_5 \cdot h_1^{(1)}+w_6 \cdot h_2^{(1)} \\
& =1.0 \cdot 1.0+2.0 \cdot 0.95 \\
& =2.9
\end{aligned}
$$
（3）计算损失: 根据数据真实值 $y=0.8$ 和平方差损失函数来计算损失
$$
\begin{aligned}
\delta & =\frac{1}{2}\left(y-y^{\prime}\right)^2 \\
& =0.5(0.8-2.9)^2 \\
& =2.205
\end{aligned}
$$
（4）计算梯度: 此过程实际上就是计算偏微分的过程, 以参数 $w_5$ 的偏微分计算为例, 如下图
根据链式法则:
$$
\frac{\partial \delta}{\partial w_5}=\frac{\partial \delta}{\partial y^{\prime}} \cdot \frac{\partial y^{\prime}}{\partial w_5}
$$
其中:
$$
\begin{aligned}
\frac{\partial \delta}{\partial y^{\prime}} & =2 \cdot \frac{1}{2} \cdot\left(y-y^{\prime}\right)(-1) \\
& =y^{\prime}-y \\
& =2.9-0.8 \\
& =2.1 \\
y^{\prime} & =w_5 \cdot h_1^{(1)}+w_6 \cdot h_2^{(1)} \\
\frac{\partial y^{\prime}}{\partial w_5} & =h_1^{(1)}+0 \\
& =1.0
\end{aligned}
$$
所以:
$$
\frac{\partial \delta}{\partial w_5}=\frac{\partial \delta}{\partial y^{\prime}} \cdot \frac{\partial y^{\prime}}{\partial w_5}=2.1 \times 1.0=2.1
$$
类似的，如果以参数 $w_1$ 为例子, 它的偏微分计算就也用到链式法则, 过程如下所示。
$$
\begin{gathered}
\frac{\partial \delta}{\partial w_1}=\frac{\partial \delta}{\partial y^{\prime}} \cdot \frac{\partial y^{\prime}}{\partial h_1^{(1)}} \cdot \frac{\partial h_1^{(1)}}{\partial w_1} \\
y^{\prime}=w_5 \cdot h_1^{(1)}+w_6 \cdot h_2^{(1)} \\
\frac{\partial y^{\prime}}{\partial h_1^{(1)}}=w_5+0 \\
=1.0 \\
h_1^{(1)}=w_1 \cdot x_1+w_2 \cdot x_2 \\
\frac{\partial h_1^{(1)}}{\partial w_1}=x_1+0 \\
\frac{\partial \delta}{\partial w_1}=\frac{\partial \delta}{\partial y^{\prime}} \cdot \frac{\partial y^{\prime}}{\partial h_1^{(1)}} \cdot \frac{\partial h_1^{(1)}}{\partial w_1}=2.1 \times 1.0 \times 0.5=1.05
\end{gathered}
$$
（5）梯度下降更新网络参数：假设这里的超参数 “学习速率” 的初始值为 0.1 , 根据梯度下降的更新公式, $w_1$ 参数的更新计算如下所示:
$$
w_1^{\text {(update) }}=w_1-\eta \cdot \frac{\partial \delta}{\partial w_1}=1.0-0.1 \times 1.05=0.895
$$
同理, 可以计算得到其他的更新后的参数:
$$
w_1=0.895, w_2=0.895, w_3=0.29, w_4=0.28, w_5=0.79, w_6=1.8005
$$
到此为止, 我们就完成了参数迭代的全部过程。可以计算一下损失看看是否有减小, 计算如下:
$$
\begin{aligned}
\delta & =\frac{1}{2}\left(y-y^{\prime}\right)^2 \\
& =0.5(0.8-1.3478)^2 \\
& =0.15
\end{aligned}
$$
此结果相比较于之间计算的前向传播的结果 2.205 , 是有明显的减小的。
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
# 1. 超参数设置
batch\_size = 64
learning\_rate = 0.001
num\_epochs = 2 # 这里为了示例，训练轮数设得较小，可自行增大
# 2. 数据加载与预处理
# MNIST 是 28x28 的灰度图像，这里使用随机裁剪、归一化等简单变换
transform = transforms.Compose([
transforms.ToTensor(), # 将 PIL Image 或 numpy.ndarray 转换为张量
transforms.Normalize((0.1307,), (0.3081,)) # 使用 MNIST 官方推荐均值和方差进行归一化
])
train\_dataset = torchvision.datasets.MNIST(
root='./data',
train=True,
transform=transform,
download=True
)
test\_dataset = torchvision.datasets.MNIST(
root='./data',
train=False,
transform=transform,
download=True
)
train\_loader = torch.utils.data.DataLoader(
dataset=train\_dataset,
batch\_size=batch\_size,
shuffle=True
)
test\_loader = torch.utils.data.DataLoader(
dataset=test\_dataset,
batch\_size=batch\_size,
shuffle=False
)
# 3. 定义网络结构
class SimpleNN(nn.Module):
def \_\_init\_\_(self):
super(SimpleNN, self).\_\_init\_\_()
# MNIST 输入图像大小 1x28x28，我们先将其铺平为 (batch\_size, 784)
self.flatten = nn.Flatten()
self.fc1 = nn.Linear(28 * 28, 128)
self.relu1 = nn.ReLU()
self.fc2 = nn.Linear(128, 64)
self.relu2 = nn.ReLU()
self.fc3 = nn.Linear(64, 10) # 10 类（数字 0~9）
def forward(self, x):
x = self.flatten(x)
x = self.fc1(x)
x = self.relu1(x)
x = self.fc2(x)
x = self.relu2(x)
x = self.fc3(x)
return x
# 4. 初始化模型、损失函数和优化器
device = torch.device("cuda" if torch.cuda.is\_available() else "cpu")
model = SimpleNN().to(device)
criterion = nn.CrossEntropyLoss() # 交叉熵损失常用于分类任务
optimizer = optim.Adam(model.parameters(), lr=learning\_rate)
# 5. 训练函数
def train\_one\_epoch(model, dataloader, criterion, optimizer, device):
model.train() # 设置为训练模式
running\_loss = 0.0
correct = 0
total = 0
for images, labels in dataloader:
images, labels = images.to(device), labels.to(device)
# 前向传播
outputs = model(images)
loss = criterion(outputs, labels)
# 反向传播和优化
optimizer.zero\_grad()
loss.backward()
optimizer.step()
# 统计损失和准确率
running\_loss += loss.item() * images.size(0)
\_, predicted = torch.max(outputs, 1)
correct += (predicted == labels).sum().item()
total += labels.size(0)
epoch\_loss = running\_loss / total
epoch\_acc = correct / total
return epoch\_loss, epoch\_acc
# 6. 测试函数
def evaluate(model, dataloader, criterion, device):
model.eval() # 设置为评估模式
running\_loss = 0.0
correct = 0
total = 0
# 评估阶段不需要计算梯度
with torch.no\_grad():
for images, labels in dataloader:
images, labels = images.to(device), labels.to(device)
outputs = model(images)
loss = criterion(outputs, labels)
running\_loss += loss.item() * images.size(0)
\_, predicted = torch.max(outputs, 1)
correct += (predicted == labels).sum().item()
total += labels.size(0)
epoch\_loss = running\_loss / total
epoch\_acc = correct / total
return epoch\_loss, epoch\_acc
# 7. 训练与验证
for epoch in range(num\_epochs):
train\_loss, train\_acc = train\_one\_epoch(model, train\_loader, criterion, optimizer, device)
test\_loss, test\_acc = evaluate(model, test\_loader, criterion, device)
print(f"Epoch [{epoch+1}/{num\_epochs}] "
f"Train Loss: {train\_loss:.4f}, Train Acc: {train\_acc:.4f}, "
f"Test Loss: {test\_loss:.4f}, Test Acc: {test\_acc:.4f}")
/home/arwin/anaconda3/envs/dl/lib/python3.8/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user\_install.html
from .autonotebook import tqdm as notebook\_tqdm
Epoch [1/2] Train Loss: 0.2726, Train Acc: 0.9208, Test Loss: 0.1360, Test Acc: 0.9585
Epoch [2/2] Train Loss: 0.1135, Train Acc: 0.9654, Test Loss: 0.0978, Test Acc: 0.9690
Credits
- Icons made by Becris from www.flaticon.com
- Icons from Icons8.com - https://icons8.com
- Datasets from Kaggle - https://www.kaggle.com/
- Jason Brownlee - Why Initialize a Neural Network with Random Weights?
- OpenAI - Deep Double Descent
- Tal Daniel
作者
arwin.yu.98@gmail.com