SE(3)-Transformers

SE(3)-Transformers: 3D Roto-Translation Equivariant Attention Networks是一篇研究如何在三维空间中实现旋转和平移等变性的深度学习网络的工作。这种网络通过结合\(SE(3)\)群的等变性，将传统的Transformer结构扩展到了三维空间，从而在不牺牲表达能力的前提下，显著提升了对三维几何信息的建模能力。此项工作为在三维空间中的物理模拟、生物信息学以及计算机视觉等领域的应用提供了强大的工具。

1、SE(3)-Transformer的计算流程

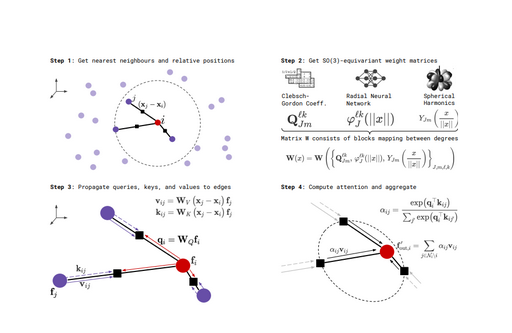
图1展示了一个用于\(SE(3)\)-Transformer等变注意力机制的工作流程。该流程分为四个步骤：首先获取节点的最近邻居及其相对位置，然后通过\(SE(3)\)等变权重矩阵进行特征映射，接着将查询、键和值向量传递到边上，最后通过注意力机制计算并聚合邻居节点的信息。整个过程确保了在旋转等变性下节点特征的更新，适用于需要保持空间对称性的图形数据处理任务。

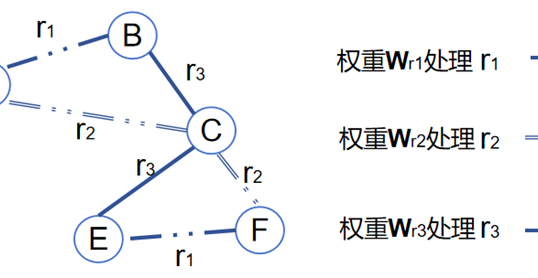
在第一步中，节点\(\mathrm{i}\)的最近邻居（节点\(\mathrm{j}\)）及其相对位置\(x_{j}-x_{i}\)被获取。最近邻居通常通过在三维空间中的某个距离度量来定义，图1中节点\(\mathrm{i}\)和它的邻居节点\(\mathrm{j}\)以向量的形式表示它们之间的相对位置。

在第二步中，重点在于构造\(SE(3)\)等变的权重矩阵\(W(x)\)，这是为了确保在\(SE(3)\)群的选择操作下，模型的输出结果保持不变。具体而言，权重矩阵\(W(x)\)是通过结合Clebsch-Gordan系数\(\varrho_{Jm}^{\ell k}\)、径向神经网络\(\varphi_J^{\ell k}(\parallel x\parallel)\)和球谐函数\(Y_{Jm}\left(\frac{x}{\parallel x\parallel}\right)\)来构建的。Clebsch-Gordan系数用于处理不同角动量态之间的耦合关系，径向神经网络则基于距离\(\left|x\right|\)来建模径向特征，而球谐函数用于处理角度方向上的信息。通过这些成分的组合，构建出的权重矩阵能够确保特征在旋转操作下依然保持\(SE(3)\)等变性。这一矩阵为后续计算中的查询、键和值向量提供了基础，使得模型能够在处理三维空间中的数据时保持旋转对称性，即对数据进行旋转时输出结果不会发生改变。这对于处理具有空间对称性的数据（如3D点云、分子结构等）尤其关键。

在第三步中，模型通过\(SE(3)\)等变权重矩阵将节点的特征向量映射为査询（query）、键（key）和值（value）向量，并将这些向量传递到图的边上。具体来说，给定目标节点\(\mathrm{i}\)的特征向量\(f_{i}\)和其邻居节点\(\mathrm{j}\)的特征向量\(f_{j}\)，模型首先利用相对位置（\(x_j-x_i\)）结合特征\(f_{j}\)，通过等变权重矩阵\(W_{K}\)和\(W_{V}\)生成键向量\(k_{ij}\)和值向量\(\boldsymbol{v}_{{ij}}\)。同时，目标节点\(\mathrm{i}\)的查询向量\(q_{i}\)由其自身特征向量\(f_{i}\)通过另一权重矩阵\(W_{Q}\)生成。这个过程确保了在图的每条边上都有与目标节点和邻居节点相关联的查询、键和值向量，且这些向量的生成过程具有\(SE(3)\)等变性，即在旋转和平移操作下保持不变。这一机制为后续的注意力计算和信息聚合奠定了基础，使得模型能够有效地捕捉邻居节点对目标节点的影响，并保证结果的空间变换不变性。

在第四步中，模型利用先前计算的查询、键和值向量，通过注意力机制对邻居节点的信息进行加权聚合。具体来说，目标节点\(\mathrm{i}\)和其邻居节点\(\mathrm{j}\)之间的注意力权重\(\alpha_{ij}\)是通过目标节点的查询向量\(q_{i}\)和邻居节点的键向量\(k_{ij}\)的点积计算得出的，表达式为：

\(\alpha_{ij}=\frac{\exp(q_i^\top k_{ij})}{\sum_{j^{\prime}}\exp(q_i^\top k_{ij^{\prime}})}\)

这种注意力权重反映了目标节点\(\mathrm{i}\)对邻居节点\(\mathrm{j}\)信息的关注程度。随后，目标节点的输出特征\(f_{\mathrm{out},i}\)是对所有邻居节点的信息（即值向量\(\boldsymbol{v}_{{ij}}\)）进行加权求和后的结果，公式为：

\(\boldsymbol{f}_{out,i}=\sum_{j\in\mathcal{N}(i)}\alpha_{ij}\boldsymbol{\nu}_{ij}\)

通过这种加权求和的方式，模型能够聚合邻居节点的信息，并通过注意力机制来突出对目标节点最相关的信息。这一步确保了在\(SE(3)\)群的旋转和平移操作下，聚合后的节点特征保持等变性，即在空间变换下，节点的最终特征仍然不变，从而增强了模型在处理具有空间对称性的数据（如3D点云、分子结构等）时的鲁棒性和准确性。

2、SE(3)-Transformer的组成部分

\(SE(3)\)-Transformer 主要包括以下三个部分：

1. 边缘注意力权重\(\alpha_{ij}\)：这一部分的作用是构建边缘的注意力权重\(\alpha_{ij}\)，以确保每条边\(\mathrm{ij}\)所传递的信息在\(SE(3)\)变换下保持不变。换句话说，这一机制能够使得无论在何种旋转或平移下，边\(\mathrm{ij}\)的信息仍能保持一致。

2. 信息传递机制\(\nu_{ij}\)：该机制沿着边缘传递信息\(\nu_{ij}\)，这些信息是\(SE(3)\)等变的信号。该信息的计算方式源自TFN卷积中的提取信号。具体来说，信息\(\nu_{ij}\)是通过对输入特征进行线性变换和与节点间的相对位置向量（ \(x_j-x_i\)）结合后得到的。

3. 线性/注意力自交互层：在每个节点的邻域上执行注意力机制。

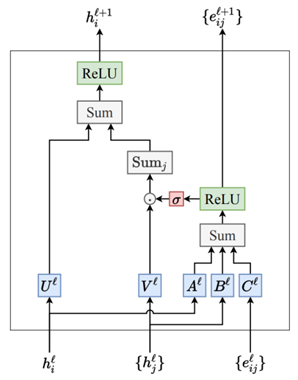
公式定义如下所示：

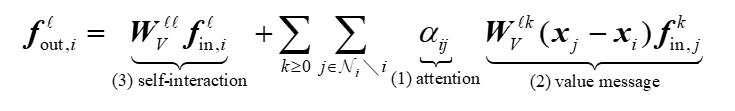
其中：

（1）\(W_V^\ell f_{\mathrm{in},i}^\ell\)是自交互部分。

（2）\(\sum\alpha_{ij}W^{\ell k}V(x_j-x_i)r_{\mathrm{in},j}^k\)是由注意力权重和\(SE(3)\)等变消息构成的部分。

注意力是在每个节点的领域\(\mathcal{N}_{i}\)上进行的，上式中：

（1）\(\alpha_{ij}\)是边\(\mathrm{ij}\)的注意力权重，它是\(SE(3)\)不变的。

（2）\(W^{\ell k}V(x_j-x_i)r_{\mathrm{in},j}^k\)是考虑了两点\(x_{j}\)和\(x_{i}\)之间的位移向量\(x_j-x_i\)后，进行的消息传播。

实际上，如果移除注意力权重\(\alpha_{ij}\)，则该机制变成了一个张量场卷积。如果移除了\(W_{V}\)对\(x_j-x_i\)的依赖，则该机制变成了传统的注意力机制。针对上述公式，首先理解注意力机制部分，注意力权重\(\alpha_{ij}\)的计算方式，具体为：

\(\alpha_{ij}=\frac{\exp(\boldsymbol{q}_i^\top\boldsymbol{k}_{ij})}{\sum_{j^{\prime}\in\mathcal{N}_i\setminus i}\exp(\boldsymbol{q}_i^\top\boldsymbol{k}_{ij^{\prime}})}\)

\(\boldsymbol{q}_i=\bigoplus_{\ell\geq0}\sum_{k\geq0}\boldsymbol{W}_Q^{\ell k}\boldsymbol{f}_{\mathrm{in},i}^k\)

\(k_{ij}=\bigoplus_{\ell\geq0}\sum_{k\geq0}W_{K}^{\ell k}(x_{j}-x_{i})f_{\mathrm{in},j}^{k}\)

注意力权重\(\alpha_{ij}\)通过Softmax 函数计算，用于在注意力机制中确定不同边的重要性。其中，\(q_{i}\)是节点\(\mathrm{i}\)的查询向量；\(k_{ij}\)是节点\(\mathrm{j}\)的键向量，结合了\(\mathrm{j}\)和\(\mathrm{i}\)之间的几何位移\(x_j-x_i\)。在查询向量\(q_{i}\)的公式表示中：\(W_{\varrho}^{\ell k}\)是线性嵌入矩阵，负责将输入特征\(r_{\mathrm{in},j}^k\)映射到不同的特征空间。直和操作\(⊕\)表示将来自不同等级（或层级）\(\ell \)的特征连接起来，形成一个综合的查询向量。类似的，在键向量\(k_{ij}\)的表示中：\(W_K^{\ell k}\)是另一个线性嵌入矩阵，负责将输入特征\(r_{\mathrm{in},j}^k\)和几何位移\(x_j-x_i\)结合起来，生成键向量，这也通过直和操作将不同等级的特征连接起来。

公式中注意力权重\(\alpha_{ij}\)是\(SE(3)\)不变的，这是因为：如果输入特征\(r_{\mathrm{in},j}\)是\(SO(3)\)等变的，那么通过线性嵌入矩阵\(W_{\varrho}^{\ell k}\)和\(W_K^{\ell k}\)生成的查询向量\(\boldsymbol{q}_{i}\)和键向量\(k_{ij}\)也将保持\(SE(3)\)等变性。键向量中的几何位移\(x_j-x_i\)进一步确保了在三维空间中的等变性。

解释完注意力机制以后，再关注一下公式中关于value message的计算。这个术语来自注意力机制中的概念。在传统的注意力机制中，value是要传递的信息，而query和key用于计算注意力权重。在\(SE(3)\)-Transformer中，这个值消息不仅依赖于节点的特征\(f_{\mathrm{in},j}^k\)，还结合了几何位移\(x_j-x_i\)，通过\(W_{V}^{\ell k}\)的变换来生成一个新的特征表示。这种设计允许模型在捕捉节点之间的几何关系时保持\(SE(3)\)的等变性，公式表示如下：

\(W_V^{\ell k}(x_j-x_i)f_{\mathrm{in},j}^k\)

上述公式的每一部分表示如下：

（1）\(f_{\mathrm{in},j}^k\)：节点\(\mathrm{j}\)上的输入特征，\(\mathrm{k}\)表示该特征属于某个特定的阶数，即球谐函数不同阶数的特征表示，这个特征向量包含了关于节点\(\mathrm{j}\)的信息。

（2）\(x_j-x_i\)：从节点\(\mathrm{i}\)到节点\(\mathrm{j}\)的位移向量，表示节点\(\mathrm{j}\)和\(\mathrm{i}\)在三维空间中的相对位置。这个向量的长度和方向都对模型的计算有影响，特别是在处理具有几何结构的数据时。

（3）\(W_V^{\ell k}(x_j-x_i)\)：一个线性嵌入矩阵，它依赖于节点\(\mathrm{j}\)和节点\(\mathrm{i}\)之间的位移\(x_j-x_i\)。这个矩阵的作用是将输入特征\(f_{\mathrm{in},j}^k\)映射到另一个特征空间，通常是为了捕捉空间关系和等变性。

最后，解释一下自交互层。\(SE(3)\)-Transformer可以扩展为多通道特征，每个通道存储的是不同阶数\(\ell\)的特征（源于球谐函数不同阶的特征）。自交互层负责在同一节点内部和同一阶数\(\ell\)特征内进行信息的交换，只关注目标节点自身的特征更新，不考虑节点之间的关系，类似于卷积神经网络中的1×1卷积操作。具体来说，自交互层有两种实现形式。一种是线性自交互（Linear Self-interaction），公式表示为：\(f_{\mathrm{out},i,c^{\prime}}^\ell=\sum_cw_{i,c,c^{\prime}}^{\ell\ell}f_{\mathrm{in},i,c}^\ell\)，其中输出通道\(f_{\mathrm{at},i,c^{\prime}}^\ell\)是输入通道\(f_{\mathrm{in},i,c}^{\ell}\)的线性组合，这种组合是通过一个固定的权重矩阵\(w_{i,c,c^{\prime}}^{\ell\ell}\)实现的。该权重矩阵是共享的，且在所有层和通道上保持不变。另一种是注意力自交互（Attentive Self-interaction），表示为：\(\boldsymbol{w}_{i,c^{\prime},c}^{\ell\ell}=\mathrm{MLP}\left(\bigoplus_{c,c^{\prime}}f_{\mathrm{in},i,c^{\prime}}^{\ell\top}f_{\mathrm{in},i,c}^{\ell}\right)\)，该公式提出了注意力自交互的扩展形式，结合了自交互和非线性。注意力自交互通过多层感知机替换了线性权重\(w_{i,c,c^{\prime}}^{\ell\ell}\)，从而引入了非线性特性。这里，注意力权重是通过输入特征之间的内积来计算的，由于这些权重是\(SE(3)\)等变的，确保了在相同表示下的特征的内积不变性。

3、SE(3)-Transformer小结

\(SE(3)\)-Transformer 是一种结合了\(SE(3)\)等变性和注意力机制的神经网络架构。为了更好地理解\(SE(3)\) -Transformer 的独特之处，我们可以通过与TFN（Tensor Field Network）和 SEGNN （Spherical Equivariant Graph Neural Network）的对比来总结它的优势和特点。

TFN通过将输入的三维点云或分子信息表示为张量场，并使用旋转和平移等变的神经网络来处理这些信息。它能够捕捉输入数据中的对称性，并且通过张量的不同阶数（0阶标量场、1阶矢量场等）来表示不同的物理量。其优点是能够自然地处理旋转和反射等对称性问题。在物理模拟和分子建模中表现良好，特别是在需要保持物理不变量的任务中。另一方面，TFN的计算复杂度较高，尤其是当涉及高阶张量场时。对于较大的点云数据或复杂的分子结构，训练和推理的效率可能较低。

SEGNN结合了图神经网络（GNN）和球谐函数，利用球对称性的特点来处理三维几何数据。它通过在图的每个节点上使用球谐展开，将数据映射到球面上，然后通过等变的图卷积层进行特征提取。对球对称性的有效处理使其在三维数据中表现出色。通过结合图神经网络和球谐函数，能够捕捉到节点之间复杂的几何关系。但是，与TFN类似，由于涉及球谐展开，SEGNN在实现和优化上有一定的复杂性。而且，对于非球形对称的数据，可能无法充分利用其球谐展开的优势。

\(SE(3)\)-Transformer是基于Transformer架构的模型，旨在处理具有\(SE(3)\)对称性的三维点云或分子数据。 群包括平移、旋转和反射，\(SE(3)\)-Transformer通过在自注意力机制中引入 等变性，能够在复杂的三维空间中进行高效的特征提取和表示学习。\(SE(3)\)-Transformer结合了Transformer架构的高效性和\(SE(3)\)等变的特性，能够在处理三维几何数据时保持模型的灵活性和性能。在需要处理大规模三维数据时表现优越，特别是在点云和分子结构分析领域，而且具有较强的泛化能力，能够适应不同的任务和数据类型。但是其对训练数据的需求较高，可能需要较大的数据集来充分发挥模型的能力。