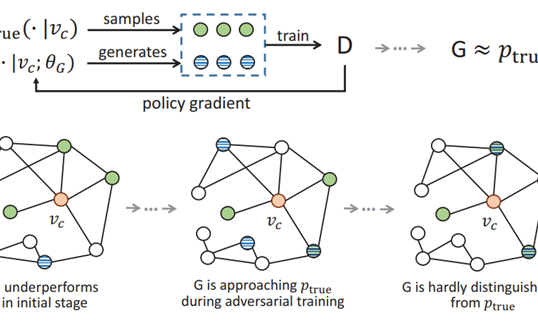
Residual Gated Graph Convnets

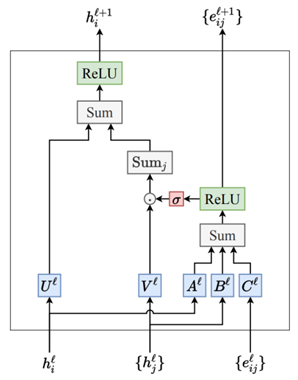
Gated GCN 结合了GCNs的空间聚合能力和LSTM中的门控机制。这种结构设计旨在解决传统GCN在处理复杂图数据时面临的信息过载和信息损失问题。每个节点的状态更新不仅依赖于其邻居的信息，还受到门控机制的控制。这种操作使得网络可以在每一层学习到如何最有效地聚合邻近节点的信息，同时根据任务的需要丢弃无关信息，使其能够适应不同的图结构和动态变化的图数据，提供了更精细的信息处理能力。Gated GCN的模型设计如图1所示。

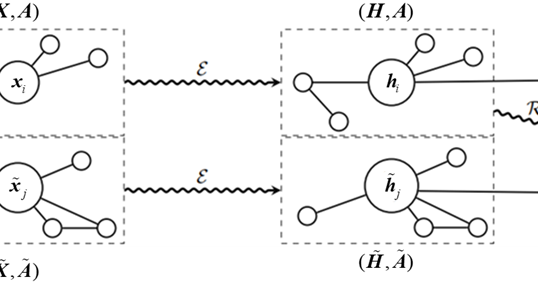
从图1中可以看到节点特征向量$h_i$和边特征向量$e_{ij}$的具体数据更新流程。首先每个节点$\mathrm{i}$在每一层$\mathrm{l}$有一个特征表示$h_i^l$，节点$\mathrm{i}$邻居节点的特征向量集合为$\left\{\begin{array}{c}{h}_j^l\end{array}\right\}$。每条边$(i,j)$在每一层$\mathrm{l}$也有一个特征表示${\mathit{e}}_{ij}$。节点特征$h_i^l$通过矩阵$U^l$和$A^l$转换。相邻节点的特征$\left\{\begin{array}{c}{h}_j^l\end{array}\right\}$通过矩阵$V^l$和$B^l$转换。边特征$\left\{\begin{array}{c}{e}_{ij}^l\end{array}\right\}$通过矩阵$C^l$转换，这里的矩阵实际上是神经网络层中的参数矩阵。节点特征$h_i^l$、邻居节点的特征$\left\{\begin{array}{c}{h}_j^l\end{array}\right\}$和边特征$\left\{\begin{array}{c}{e}_{ij}^l\end{array}\right\}$分别经过$A^l$、$B^l$和$C^l$映射后的新特征表示将进行求和（Sum）操作，这一步的含义是进行边特征与节点特征的信息交互和融合，求和后的结果会经过激活函数ReLU的处理。处理后的结果一方面作为更新后的边特征$\left\{\begin{array}{c}{\mathit{e}}_{ij}^{l+1}\end{array}\right\}$；另一方面将经过Sigmoid函数$\sigma$的处理产生一个门控信号，这个门控信号与相邻节点特征的加权（经过$V^l$变换后的$h_j^l$）和相乘，实际上是对每个邻居节点的贡献进行缩放。这就是门控机制，它控制着信息的流向，与LSTM中的门控机制类似。最终，门控后的信息被累加到当前节点特征上 （经$U^l$变换后的$h_i^l$），通过一个求和（Sum）操作。结果再次通过ReLU激活函数得到当前层的输出结果。

经过上述处理后得到的结果${\mathit{h}}_i^{l+1}$是节点$\mathrm{i}$在下一层$\mathrm{l}+1$的新特征表示。同时，边的特征也更新为$e_{ij}^{l+1}$。这个过程体现了Gated GCN在图卷积中加入门控机制的重要性。通过调节门控信号，模型能够控制每个节点在其邻居之间传递的信息量，这样就可以捕捉到图中更加复杂的结构模式，同时减少不必要的信息传递，提高了模型的泛化能力和处理大规模图数据的效率。