SimAM
基本信息
- 📰标题: SimAM: A Simple, Parameter-Free Attention Module for Convolutional Neural Networks
- 🖋️作者: Lingxiao Yang
- 🏛️机构: 1 Sun Yat-sen University (中山大学), 2 Key Laboratory of Machine Intelligence and Advanced Computing (机器智能与先进计算教育部重点实验室), 3 Guangdong Provincial Key Laboratory of Big Data Analysis and Processing (广东省大数据分析与处理重点实验室)
- 🔗链接: -
- 🔥关键词: Attention Mechanism, Convolutional Neural Networks, Parameter-Free
摘要概述
| 项目 | 内容 |
|---|---|
| 📖研究背景 | 现有注意力模块通常依赖复杂结构或额外参数,限制了效率和泛化能力。 |
| 🎯研究目的 | 提出一种无需可学习参数的简单注意力机制(SimAM),提升CNN性能。 |
| ✍️研究方法 | 基于神经科学理论,通过能量函数推导3D注意力权重,直接优化特征显著性。 |
| 🕊️研究对象 | 卷积神经网络中的特征图。 |
| 🔍研究结论 | SimAM在多个基准任务(分类/检测/分割)中优于现有注意力模块,计算开销低。 |
| ⭐创新点 | 1) 无参设计 2) 理论驱动的能量最小化框架 3) 即插即用且高效。 |
背景
-
研究背景:
卷积神经网络(ConvNets)在大规模数据集(如ImageNet)上的训练显著提升了图像分类、目标检测等视觉任务的性能。现代ConvNet通常由多阶段模块化结构组成,但设计高效模块需依赖专家经验或自动搜索策略,成本高昂。 -
过去方案:
-
模块设计:主流方法包括堆叠卷积、残差连接(ResNet)和密集连接(DenseNet),但需复杂人工设计;
-
注意力机制:如SE模块通过通道注意力增强特征,但仅限单一维度(通道或空间),且依赖启发式结构(如池化操作),灵活性不足;
-
3D权重生成:已有工作尝试生成3D权重,但采用手工编码器-解码器结构,计算效率低。
- 研究动机:
为解决现有注意力模块的局限性(维度单一、结构复杂),受神经科学启发,提出一种基于能量函数的无参3D注意力机制(SimAM),直接优化特征显著性,实现高效即插即用的特征增强。
方法
-
理论背景:
SimAM受哺乳动物大脑的空间抑制现象(spatial suppression)启发,即显著神经元会抑制周围神经元的放电活动。该模块通过量化神经元与其周围神经元的线性可分性(linear separability)来评估其重要性。 -
技术路线:
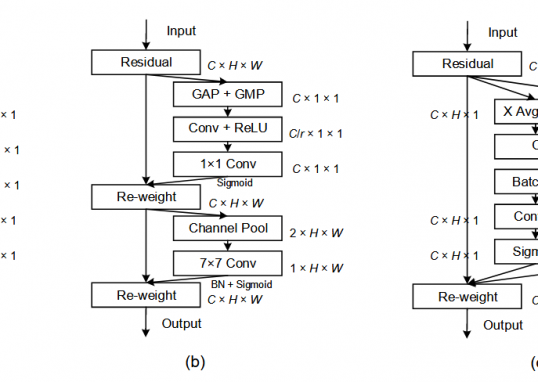
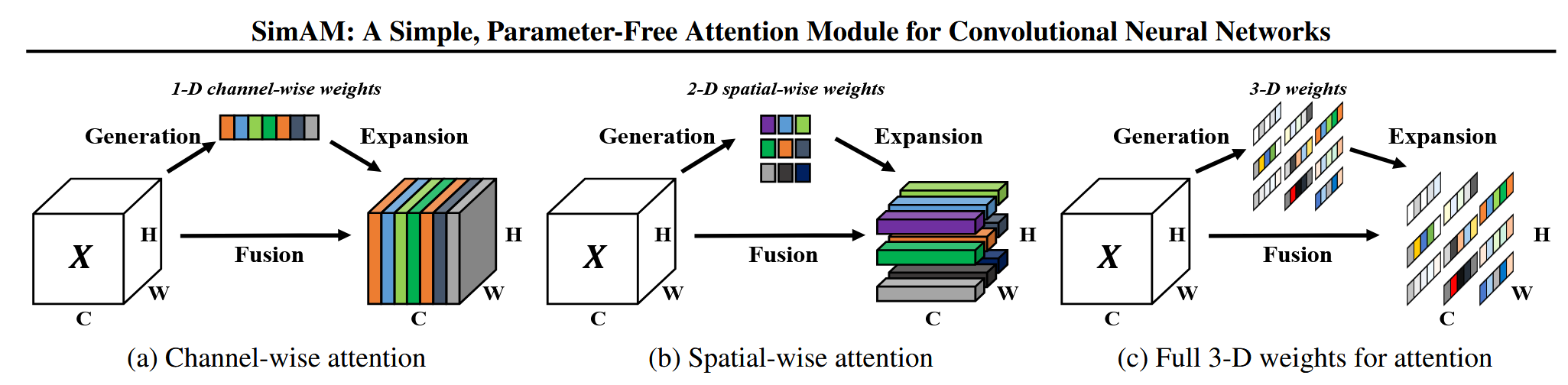
不同于现有方法(如SE、CBAM)仅生成1D(通道)或2D(空间)权重,SimAM直接推断3D注意力权重(同时考虑通道和空间维度),更贴合人脑的注意力机制(特征与空间注意力共存)

- 能量函数构建:
$$
e_t\left(w_t, b_t, y, x_i\right)=\left(y_t-\hat{t}\right)^2+\frac{1}{M-1} \sum_{i=1}^{M-1}\left(y_o-\hat{x}_i\right)^2
$$
- 目标:衡量目标神经元 $t$ 与同一通道内其他神经元 $x_i$ 的线性可分性。
- 变量:
$\circ \hat{t}=w_t t+b_t$ 和 $\hat{x}_i=w_t x_i+b_t$ 是对 $t$ 和 $x_i$ 的线性变换。 - $y_t$ 和 $y_o$ 是二元标签(如1和-1),分别表示目标神经元与其他神经元的理想输出。
- $M=H \times W$ 是通道内的神经元数量。
- 意义:最小化该能量函数时,目标神经元 $t$ 的输出趋近于 $y_t$ ,而其他神经元趋近于 $y_o$ ,从而实现区分。
- 引入正则化的能量函数
$$
e_t\left(w_t, b_t, y, x_i\right)=\frac{1}{M-1} \sum_{i=1}^{M-1}\left(-1-\left(w_t x_i+b_t\right)\right)^2+\left(1-\left(w_t t+b_t\right)\right)^2+\lambda w_t^2
$$
- 改进:
- 设定 $y_t=1$ 和 $y_o=-1$ ,明确区分目标与周围神经元。
- 加入L2正则项 $\lambda w_t^2$ 防止过拟合。
- 生物学依据:模拟空间抑制现象,即显著神经元会抑制周围神经元的激活。
- 闭式解
通过最小化公式2,作者推导出闭式解:
1.权重 $w_t$ 的解:$w_t=-\frac{2\left(t-\mu_t\right)}{\left(t-\mu_t\right)^2+2 \sigma_t^2+2 \lambda}$
- $\mu_t$ 和 $\sigma_t^2$ 是排除 $t$ 后其他神经元的均值和方差。
- 分母中的 $\lambda$ 平衡了局部差异与全局稳定性。
2.偏置 $b_t$ 的解:$b_t=-\frac{1}{2}\left(t+\mu_t\right) w_t$
-由线性变换的对称性推导而来,简化计算。
- 最小能量的计算
$$
e_t^*=\frac{4\left(\hat{\sigma}^2+\lambda\right)}{(t-\hat{\mu})^2+2 \hat{\sigma}^2+2 \lambda}
$$
- 简化假设:同一通道内所有神经元共享相同的均值 $\hat{\mu}$ 和方差 $\hat{\sigma}^2$(基于Hariharan等(2012)[1]的分布假设)。
- 能量与重要性:能量 $e_t^$ 越低,神经元 $t$ 越显著(与周围差异大),其重要性 $1 / e_t^$ 越高。
- 特征细化
$$
\tilde{X}=\operatorname{sigmoid}\left(\frac{1}{E}\right) \odot X
$$
- 操作:通过Sigmoid函数将能量倒数转换为注意力权重,按元素乘以原始特征 $X$ 。
- 优势:无需额外参数,仅需逐元素计算,高效且易于实现(如图3的PyTorch代码所示)。
结论
-
本研究基于哺乳动物大脑神经科学理论(空间抑制理论),提出无参数注意力模块SimAM,为视觉任务中的特征优化提供了理论驱动的新范式,克服了传统注意力机制依赖启发式设计的局限性。
-
优点:
1) 理论解释性强(能量函数建模神经元显著性);
2) 计算高效(闭式解避免迭代);
3) 即插即用(无需结构调整)。 -
缺点:未讨论能量函数在极端特征分布下的鲁棒性。
-
主要结论:
- 通过空间抑制理论构建能量函数,实现神经元重要性的量化;
- 推导出能量函数的解析解,显著降低计算复杂度;
- 实验验证SimAM在多种视觉任务(分类/检测等)中优于现有注意力模块。
作者
arwin.yu.98@gmail.com