PAINN

1.PAINN的向量信息的引入

PAINN（Polarizable Atom Interaction Neural Networks）可极化原子相互作用神经网络，通过考虑原子间的可极化相互作用来预测分子的性质。这种模型的开发旨在克服传统图神经网络在化学建模中的一些局限性，尤其是在描述电荷转移和极化效应方面。PAINN 的伟大在于，它是第一个将等变模型调参到超越不变模型的。

PAINN在输入数据的Embedding阶段不仅使用标量形式，还采用了向量形式。这种方法的核心思想是通过更丰富的表示来捕捉分子内部的复杂相互作用，这是传统的基于标量的方法难以实现的。例如，在化学中，分子的属性通常被描述为旋转不变的标量，例如，分子的总电荷。然而，有些属性是仅用标量表示不了的，比如一个分子的电荷分布情况，需要从单极（电荷q ）、偶极（ μ ）、到四极矩（Q ）以及更高阶的项进行多极展开来量化，公式表示如下：

\(n(r)=q+\mu^\top r+r^\top Qr+...\)                                       (1)

这个例子展示的是分子属性的复杂性，表明仅使用标量（如电荷 q ）无法完全描述分子的物理特性。PAINN模型在对输入数据的处理阶段，通过在传统的标量Embedding基础上，加入向量的Embedding，使得模型能够捕捉到分子属性的这种复杂性。具体来说，基于向量形式的特征，可以通过对向量的简单加和，既能完成角度信息的引入，同时能将计算角度的计算复杂度从\(O(\mathrm{nk}^{2})\)降至\(O(\mathrm{nk})\)，如表1所示。

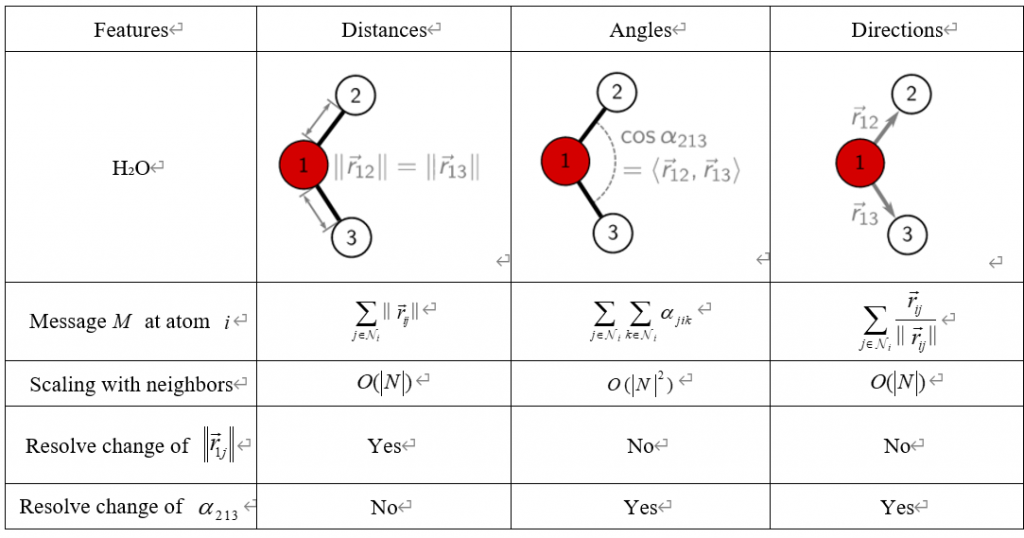
表1展示了一个模型如何处理分子H₂O中有关原子间距离、角度和方向的不同几何特征。其中编号1的原子是氧原子，而编号2和3的原子是氢原子。

第一列显示了原子1到原子2和原子3的键长，使用了欧几里得距离的标准。在神经网络中，对于每个原子\(\mathrm{i}\)，它会计算出与它邻接的所有原子 \(\mathrm{j}\) 之间的距离的总和，这个复杂度是\(O(|N|)\)，其中 \(\mathrm{N}\) 是邻居的数量。神经网络通过这些距离来解析邻居原子的变化，但距离信息不足以解析键角\(\alpha_{213}\)的变化。

第二列考虑了原子间的角度，特别是原子2、1、3形成的键角\(\alpha_{213}\)，这通过计算向量\(r_{12}\)和\(r_{13}\)的构成的角度余弦值来表示。对于原子\(\mathrm{i}\)，这需要考虑所有邻居\(\mathrm{j}\)和\(\mathrm{k}\)之间的角度，因此复杂度增加到\(O(\left|N\right|^2)\)。这种表示能够解析角度的变化，但不解析距离的变化。

第三列展示了用向量形式表征的方向特征，它是通过邻居原子\(\mathrm{j}\)相对于原子\(\mathrm{i}\)的单位方向向量来表示的。方向信息能够被用来解析键角的变化，这一作用与直接计算原子间键角的效果是一样的，但是对比直接计算键角的计算复杂度来说，却从\(O(\left|N\right|^2)\)下降至\(O(|N|)\)，是一种更高效的考虑键角\(\alpha_{213}\)的方式。

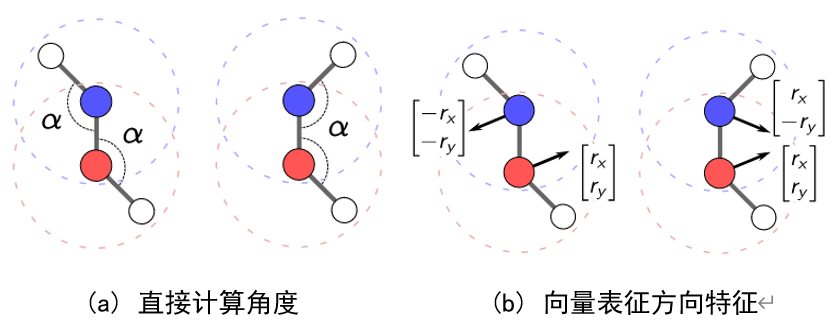
此外，作者指出：用向量表征方向特征的方式还能鉴别出更多的分子结构，如图1所示。

在图1的一对分子构象中，如果使用直接计算角度的方式进行方向特征表示则无法分别这两个分子的不同，如图1(a)所示。但如果使用向量的形式来表征方向特征，则可以很好的进行鉴别，如图1(b)所示。

2.PAINN的模型结构

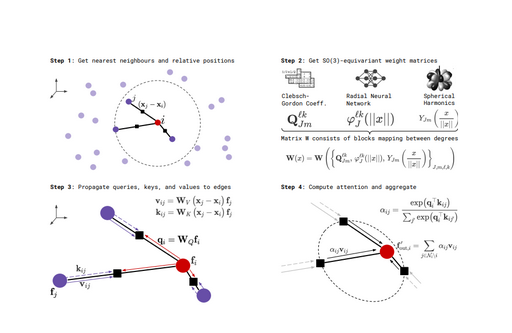
PAINN整体的模型结构如图2(a)所示，其加入特征考量的方式非常的朴素直接，就是在原子类型\(\mathbb{Z}_{i}\)和相对位置向量\(r_{ij}\)的输入基础上，加入一个初始化为0的向量作为第三种输入信息，随着网络的更迭训练自行学习相关的方向特征。接下来，通过多个message和update块的叠加来构建特征，以学习原子间的相互作用和属性。值得注意的是，在向量输入\(\nu_{i}^{0}\)和标量输入\(s_{i}^{0}\)的两个计算路径上，每个message和update块都会携带一个残差连接，帮助网络更好的进行梯度的传播。另外，位置信息\({\boldsymbol{r}}_{ij}\)也会送进每个message块中作为输入。最后一个update块的输出通过权重矩阵\(\text{W}\)和偏置向量\(\mathrm{b}\)的线性变换，经过Scaled Exponential Linear Units（SiLU）激活函数，得到最终的标量输出 。

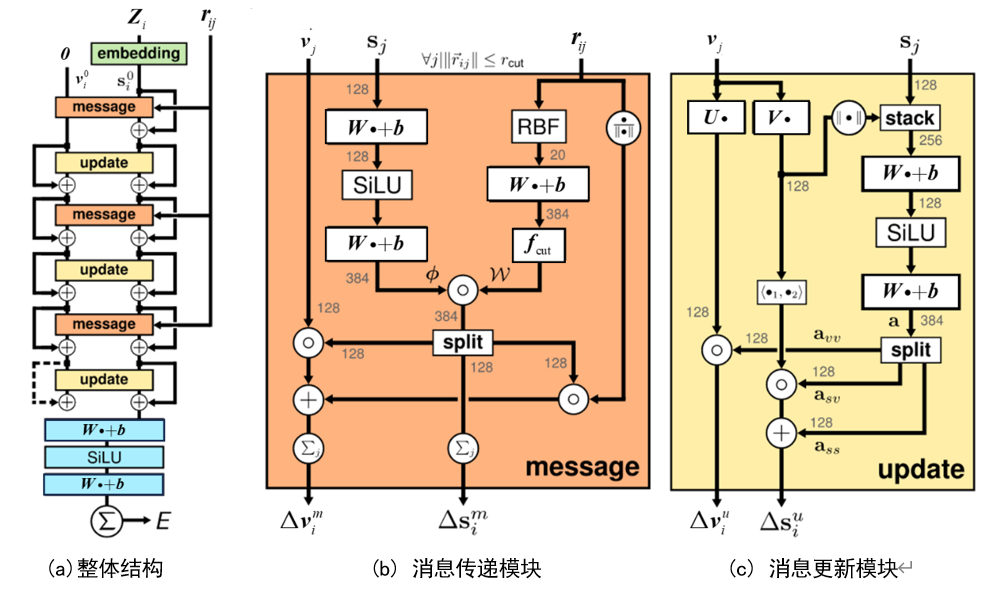
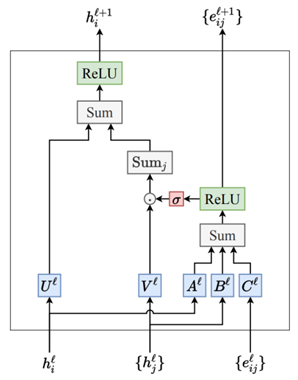
消息传递模块（Message Blocks）的详细结构如图2(b)所示。标量特征的计算是通过使用连续滤波卷积得到的，公式解释如下：

\(\begin{aligned}\Delta s_{i}^{m}&=(\phi_s(s)*W_s)_i\\&=\sum_j\phi_s(s_j)\circ W_s(\parallel r_{ij}\parallel)\end{aligned}\)                                      (2)

首先，对于每个原子\(\boldsymbol{s}_{i}\)，应用一个原子级的特征变换\(\phi_{s}\)，对应图2(b)则是中间的输入路径，这个变换由两个神经网络层和一个激活函数SiLU实现，用于将输入特征\(\boldsymbol{s}_{i}\)映射到一个新的特征空间，得到计算结果\(\phi\)。接着，这些变换后的特征\(\phi\)与一个连续卷积核生成函数的结果\(\text{W}\)进行相乘，即进行连续卷积操作。其中，\(\text{W}\)是连续卷积核，其权重数值是经过径向基函数RBF的映射，再经过神经网络的调整并结合截断函数\(f_{\mathrm{cut}}\)计算得到的。截断函数限制卷积操作时仅考虑截断半径内的原子信息，且权重根据径向函数随着距离的增加而减少。

经过连续滤波卷积的输出被分裂为三个128维的向量。一个直接作为更新后的标量特征\(\Delta\mathbf{s}_{i}^{m}\)，即式(2)的计算结果。而另外两个则参与了向量特征\(\nu_{j}\)的消息传递，向量特征\(\nu_{j}\)的消息传递公式如下所示：

\(\Delta\boldsymbol{\nu}_i^m=\sum_j\boldsymbol{\nu}_j\circ\phi_{\nu\nu}(\boldsymbol{s}_j)\circ\boldsymbol{W}_{\nu\nu}(\parallel\boldsymbol{r}_{ij}\parallel)+\sum_j\phi_{\nu s}(\boldsymbol{s}_j)\circ\boldsymbol{W}_{\nu s}^{\prime}(\parallel\boldsymbol{r}_{ij}\parallel)\frac{\boldsymbol{r}_{ij}}{\parallel\boldsymbol{r}_{ij}\parallel}\)                               (3)

从式(3)可以看出，向量特征的传递是两部分的求和，对应图2(b)中的最左边与最右边的输入分支。其中，公式的第一项对应图2(b)中的最左边的分支，即向量特征与标量特征进行连续卷积后的结果相乘，因为连续卷积是基于RBF的，其结果本身携带距离信息，因此向量特征可以从中更新到一些空间关系。而公式的第二项则对应图2(b)最右侧的分支，即连续卷积的结果乘以单位向量\(\frac{r_{ij}}{|r_{ij}|}\)（对应图中的\(\frac{\bullet}{|\bullet|}\)），这个操作导致了一个等变（方向依赖的）特征的生成。这个方向依赖的特征将加在向量信息\(\nu_{j}\)的更新路径上，通过这样的操作，模型能够在其表示中编码方向信息，从而允许模型了解原子之间的相对方向。

综上所述，更新的向量特征\(\Delta\nu_i^m\)由两个部分组成，既包含了与邻居原子间距离相关的不变特征（式3第一项），又包含了与方向信息相关的等变特征（式3第二项）。这两项的组合使得网络能够在更新过程中保持等变性。

消息更新模块（Updata Blocks）如图2(c)所示，这一模块可以对标量特征和向量特征进行相互融合。可以发现：向量特征\(\boldsymbol{\nu}_{j}\)必须要遵循线性变换，以达到遵循等变性的目的。因此\(\boldsymbol{\nu}_{j}\)仅通过一个线性的神经网络\(\boldsymbol{U}_{\bullet}\)（不包含偏置和激活函数）进行处理，然后与标量特征相乘进行信息融合即可。至于标量特征的更新，则可以进行任何的非线性处理，其目的是让标量特征学习到不变性。具体来说，标量特征\(S_{j}\)首先与经过线性层\(\boldsymbol{V}_{\bullet}\)处理的向量特征进行拼接，拼接后的结果经过两层带偏置神经网络以及一个SiLU激活函数进行标量特征和向量特征的融合，其计算结果被分成三份\(a_{\nu\nu}\)、\(a_{s\nu}\)和\(a_{ss}\)。\(a_{\nu\nu}\)与\(U•\nu_j\)的结果相乘参与向量特征\(\nu_{j}\)的更新。\(a_{s\nu}\)和\(a_{ss}\)两份分别通过加和乘的操作更新标量特征\(s_{i}\)，具体来说，\(U•\nu_j\)和\(V•\nu_{j}\)先进行点积得到一个标量，即\( \left<U \cdot \nu_j , V \cdot \nu_j \right> \)相乘的结果上，再加上\(a_{ss}\)就得到了最终更新后的标量特征。消息更新模块通过这种特定的方式处理标量特征和向量特征，以确保在更新过程中分别学习到不变性和等变性。

最后，EGNN在处理节点特征上表现的是不变性，在处理位置信息时表现的是等变性。因此，在下游任务中，如果仅使用EGNN更新后的节点特征作为输入信息，此时网络实际上表现的是不变性而不是等变性。相比之下，PaiNN在消息更新阶段，等变的向量信息和不变的节点信息是存在信息交互和混合的，即使此时仅使用PaiNN更新后的节点特征进行再进行下游任务，网络也具备等变性质。