GVP-GNN

1、Geometric Vector Perceptron

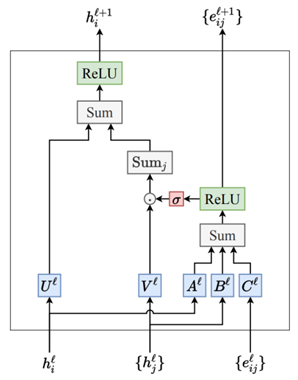
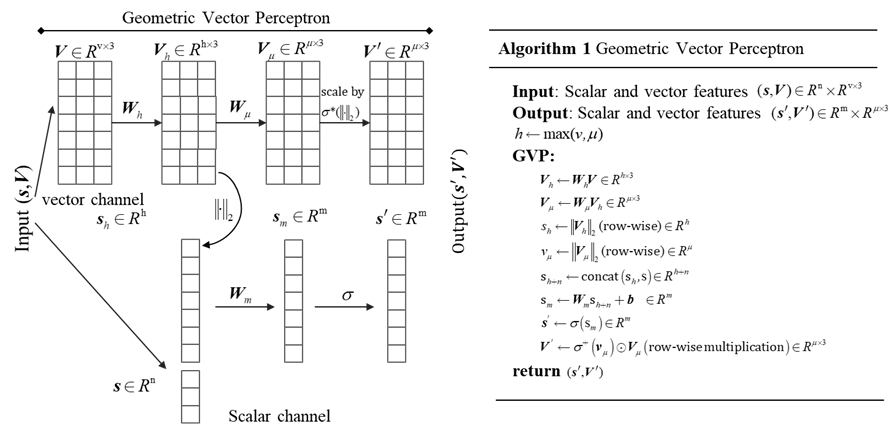
GVP-GNN包含标量和向量两个处理通道，如图1所示。向量通道处理向量特征\(\text{V}\)，这些特征是三维空间中的向量，通常代表方向性数据。\(\text{V}\)乘以权重矩阵\(W_{\nu h}\)和\(W_{\nu\mu}\)，可以分别得到两个新的向量集合 \(V_{h}\)和\(V_{\mu}\)。接着，这些向量使用L2范数进行归一化，其中\(V_{h}\)归一化后的结果与标量特征\(\text{s}\)进行拼接参与后续标量信息的更新；\(V_{\mu}\)归一化后的结果经过激活函数\(\sigma^{+}\)的处理得到一个非负的缩放因子\(\sigma^+(V_\mu)\)。激活函数\(\sigma^{+}\)可以将其视为一种修改版的ReLU函数，专门被应用于向量\(V_{\mu}\)的L2范数，得到一个非负的缩放因子，这个缩放因子起到一种门控函数的作用。具体来说，激活函数\(\sigma^{+}\)对于任何负输入和介于0与𝜖之间的输入输出一个小的正常数𝜖。对于大于𝜖的正输入，输出等于输入值。公式表示为：

\(\sigma^+(x)=\max(\epsilon,x)\)                                            (1)

缩放因子\(\sigma^{+}(V_{\mu})\)将与\(V_{\mu}\)中相对应位置的元素进行逐元素乘法，这个操作在几何学上可以被理解为按元素缩放每个向量，这种逐元素的乘法使得网络能够调整每个向量方向上的大小，而不改变其方向。结果\(V^{\prime}\)是更新后的向量特征，其维度仍然是\(R^{\mu\times3}\)，每个向量的大小已经被调整过，但方向保持不变。

值得注意的是归一化操作一般是规范向量的大小，而最后的门控机制又在调整向量的大小，这在逻辑上看起来有些自相矛盾，但实际上这两个过程是相辅相成的。具体而言，归一化处理可以确保向量的方向被保留下来，同时将它们的大小标准化到相似的规模，这主要是为了数值计算的稳定性和优化算法的效率。归一化之后的向量在进行神经网络的训练时不会因为大小差异过大而导致梯度问题。接着，尽管归一化将所有向量的大小统一，神经网络在训练过程中学习到的权重和其他参数，却可以使网络动态调整向量的大小来适应不同的任务。也就是说，网络可以决定哪些方向的特征更重要，并相应地增加这些特征向量的大小（权重），而不是通过改变它们的方向。简单说归一化的作用是提供数值稳定性和优化效率，同时保持向量方向的信息。向量大小调整是为了网络学习的过程中可以动态调整向量大小，来强调某些特征的重要性。

标量通道处理标量特征\(\text{s}\)，这些特征没有方向性，通常代表物体的大小、强度等属性。首先，标量信息\(\text{s}\)与向量通道归一化后的输出\(V_{h}\)进行拼接，形成一个新的向量\(s_{h+n}\)。然后，通过权重矩阵\(W_{m}\)进行变换，再经过一个激活函数\(\sigma\)，得到最终的输出标量特征\(s^{\prime}\)。

2、GVP结合GNN

GVP-GNN采用了GNN的信息传递机制使用GVP来更新图中节点的特性向量。下面公式逐步解析它的关键部分：

\(\boldsymbol{h}_m^{(j\to i)}:=g\left(\operatorname{concat}\left(\boldsymbol{h}_\nu^{(j)},\boldsymbol{h}_e^{(j\to i)}\right)\right)\)               (2)

\(\boldsymbol{h}_\nu^{(i)}\leftarrow\text{LayerNorm}\Bigg(\boldsymbol{h}_\nu^{(i)}+\frac1{k'}\text{Dropout}\Bigg(\sum_{j:\boldsymbol{e}_{j\to i}\in\mathcal{E}}\boldsymbol{h}_m^{(j\to i)}\Bigg)\Bigg)\)                        (3)

\(\boldsymbol{h}_\nu^{(i)}\leftarrow\text{LayerNorm}\left(\boldsymbol{h}_\nu^{(i)}+\text{Dropout}\left(g\left(\boldsymbol{h}_\nu^{(i)}\right)\right)\right)\)                          (4)

其中式(2)是消息聚合的体现，\(h_m^{(j\to i)}\)是从节点\(\mathrm{j}\)传递给节点\(\mathrm{i}\)的消息，\(\mathrm{g}\)是三个几何向量感知机，用于更新转换节点和边的特征。 \(h_{\nu}^{(j)}\)和\(h_e^{(j\to i)}\)分别表示没有被GVP更新前的节点\(\mathrm{j}\)和边\((j\to i)\)的特征。\(\mathrm{concat}\left(\boldsymbol{h}_\nu^{(j)},\boldsymbol{h}_e^{(j\to i)}\right)\)表示将节点和边的特征向量进行拼接，一起作为GVP的输入。

值得注意的是，在关于GVP的讲解中提到其输入是标量信息和向量信息两部分，而式(2又变成了节点特征\(h_{\nu}^{(j)}\)和边特征\(h_e^{(j\rightarrow i)}\)。实际上，这里的节点特征和边特征本身已经包含了标量和向量信息，只是公式中没有显示的表达而已。具体来说，节点特征\(h_{\nu}^{(j)}\)要求包含了节点的标量信息（如氨基酸的类型、电荷等） 和向量信息（如其在三维空间中的方向向量）。同理，边特征也要求包含了标量和向量信息，如连接节点的距离、方向等。

式(3)和(4)都表示节点特征的更新。在式(3)中，LayerNorm是一种规范化技术，用于标准化每个样本内部的特征，它在神经网络中常用于稳定和加速训练。\(h_{\nu}^{(i)}+\frac{1}{k^{^{\prime}}}…\)这部分表示当前节点特征\(h_{\nu}^{(i)}\) 与经过Dropout和聚合邻居信息后得到的新特征的和，这是一种典型的残差连接机制，有助于缓解梯度消失问题，并允许更深层次的网络训练。\(\frac{1}{k^{\prime}}\)是一个归一化因子，其中\({k^{\prime}}\)是实际接收到的消息数量，等于节点\(\mathrm{i}\)的邻居数量。这个因子确保了：不论节点有多少个邻居，聚合后的信息都会保持一致的规模。Dropout 是一种正则化技术，通过在训练过程中随机“丢弃”（即将参数设置为0) 一些神经元的输出来防止网络过拟合。在这里，Dropout 被应用于所有邻居节点\(\mathrm{j}\)的消息\(h_{m}^{(j\rightarrow i)}\)的总和，而不是随机选择邻居节点。总的来说，式(3)表示的是节点\(\mathrm{i}\)的特征如何通过与它的所有邻居\(\mathrm{j}\)的信息汇总（并且这个汇总的信息受到Dropout的影响）后，结合残差连接进行更新。这种更新机制允许每个节点保留自己的信息的同时也融合邻居节点的信息，从而在整个网络中传递和扩散信息。

式(4)则负责将式(3)得到的节点特征进行进一步的更新迭代，其核心步骤是\(g\left(h_{\nu}^{(i)}\right)\)。\(\mathrm{g}\)是三个几何向量感知机，对当前的节点特征\(h_\nu^{(i)}\)进行处理，进一步学习更复杂的特征变换。至于式(4)中的Dropout、LayerNorm和残差连接的作用则与式(3)类似，这里不再赘述。

3、GVP-GNN等变性的讨论

GVP-GNN模型通过融合标量和向量信息来增强对几何结构的表征能力。在该模型中，标量信息通常是不变性的，因为标量值（如温度、质量等）通常不随参考系的旋转或平移而改变。向量信息如位置或方向向量，则是等变性的，因为它们会随着参考系的旋转或平移而相应地变换。在GVP-GNN中实现等变性，是通过设计网络的操作来保持输入向量的旋转等变性。这意味着：如果输入的向量数据（如原子坐标）发生旋转，网络的向量输出也应当以相同的方式发生旋转。

GVP-GNN模型的等变性不仅仅来源于标量和向量两种处理通道，更重要的是模型的设计允许在更新节点特征时，向量信息的方向被保留并正确处理。例如，在GVP的向量处理通道中，只改变向量大小，不改变方式就是为了保证等变性。这意味着如果输入数据（如分子结构）经历了空间旋转，输出的向量特征也会以同样的方式进行旋转。而且，在向量处理通道中，也不存在非线性的操作，目的也是为了保证等变性。具体来说，向量\(\mathrm{V}\)与权重矩阵\(W_{\nu h}\)和\(W_{\nu\mu}\)相乘，得到两个新的向量集合\(V_{h}\)和\(V_{\mu}\)。这种变换是线性的，并且保持等变性。\(V_{h}\)通过L2范数归一化并与标量特征\(\mathrm{s}\)进行拼接，这个拼接操作保持向量的方向，同时为标量通道提供了大小信息。\(V_{\mu}\)通过L2范数归一化后，其结果通过激活函数\(\sigma^{+}\)（如ReLU变体）处理，生成非负的缩放因子，该因子与\(V_{\mu}\)进行逐元素乘法，这个操作在保持方向不变的同时调整大小。