Graph Convolutional Network（GCN）

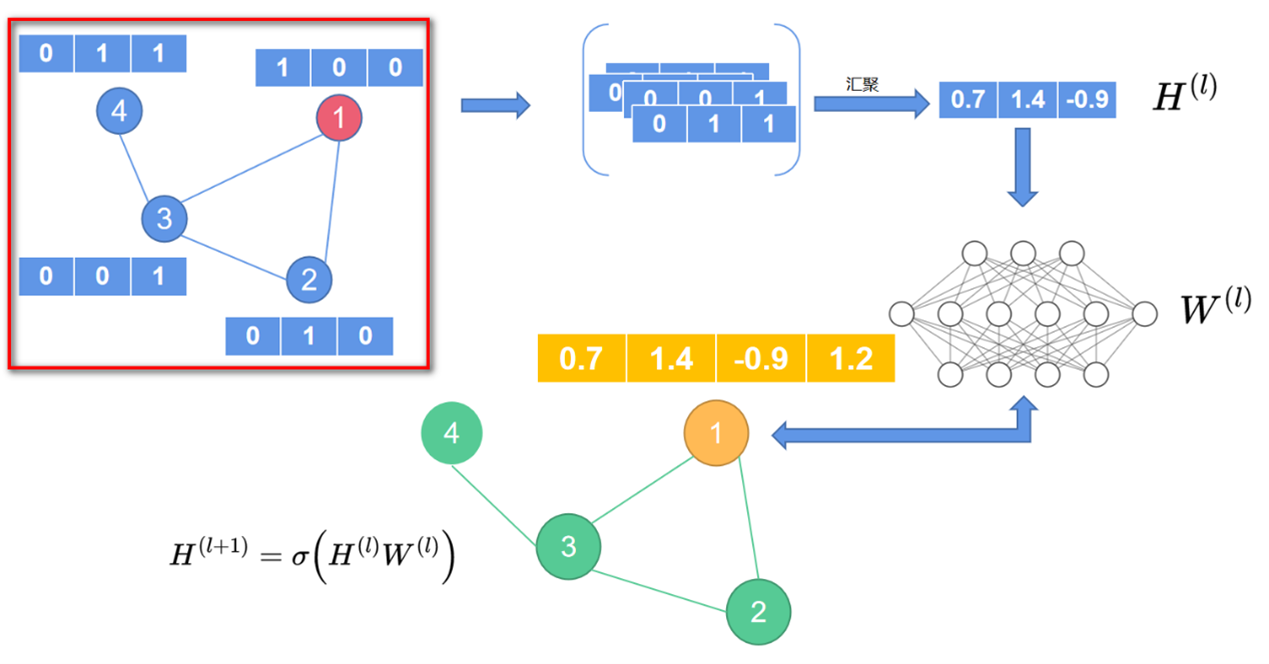
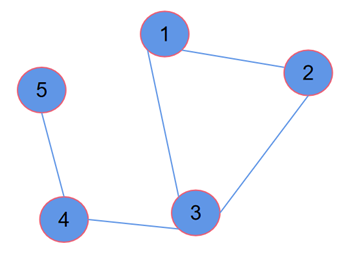
先来看一下之前讲解的朴素图神经网络，如图1所示。

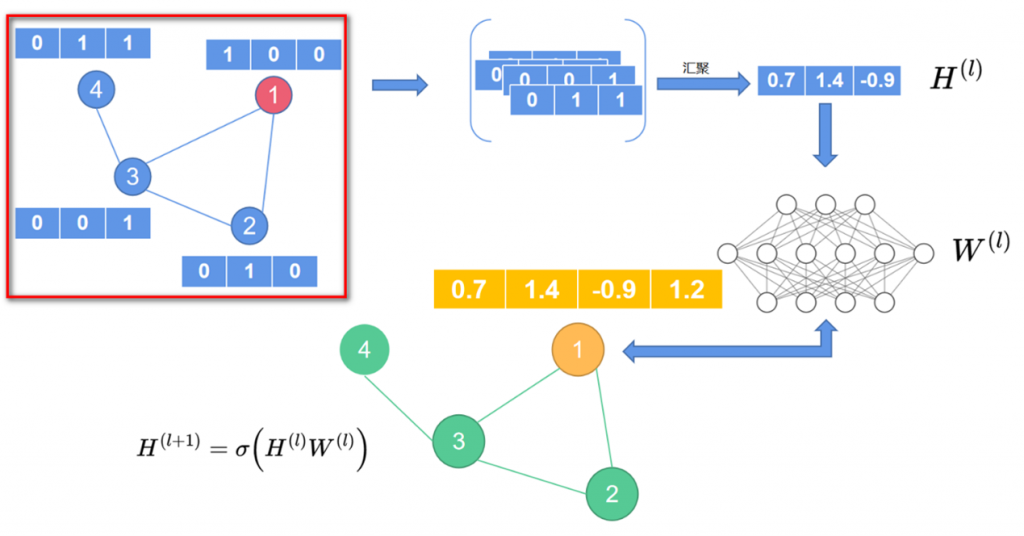
图1左上角方框部分可以看作图神经网络的初始状态。以1号节点为例，在图神经网络中，信息的传递是先汇聚一号节点的邻居节点信息，得到汇聚后的新向量，这个向量可以看作图神经网络第一层的输入信息\(H^{(l)}\)。然后\(H^{(l)}\) 经过一个 MLP 的映射, 得到一个新的输出向量\(H^{(l+1)}\) , 这个向量则作为第二层图神经网络的输入信息, 依次类推, 可以定义出一个多层的图神经网络。层与层之间的信息传递公式可以写作:

\(H^{(l+1)}=\sigma(H^{(l)}W^{(l)})\)

而图卷积神经网络的计算公式则为：

\(H^{l+1}=\sigma(\tilde{D}^{-\frac12}\tilde{AD}^{-\frac12}H(l)W(l))\)

两者最主要的区别就是图卷积神经网络比图神经网络多了一个\(\tilde{\boldsymbol{D}}^{-\frac12}\tilde{\boldsymbol{AD}}^{-\frac12}\)。其中，\(\tilde{A}=A+I_N\)， \(A\) 就是图的邻接矩阵，\(I_{N}\)是一个全一的对角矩阵，即：

\(\begin{aligned}&\boldsymbol{A}=\begin{pmatrix}0.&1.&1.&0.\\1.&0.&1.&0.\\1.&1.&0.&1.\\0.&0.&1.&0.\end{pmatrix}&\boldsymbol{I}_N=\begin{pmatrix}1.&0.&0.&0.\\0.&1.&0.&0.\\0.&0.&1.&0.\\0.&0.&0.&1.\end{pmatrix}\\&\tilde{\boldsymbol{A}}=\boldsymbol{A}+\boldsymbol{I}_N=\begin{pmatrix}1.&1.&1.&0.\\1.&1.&1.&0.\\1.&1.&1.&1.\\0.&0.&1.&1.\end{pmatrix}\end{aligned}\)

邻接矩阵 \(A\)表示的是节点与节点之间的关系，全一的对角矩阵\(I_{N}\)表示的是节点自身，所以\(\tilde{A}=A+I_N\)表示考虑了节点自身信息的邻接矩阵。

先将\(A\)矩阵加入图卷积神经网络的计算公式中，得到：

\(H^{(l+1)}=\sigma(\tilde{A}H^{(l)}W^{(l)})\)

其中，\(H^{(l)}\)的值是图1中的节点初始化向量：

\(\tilde{\boldsymbol{A}}\boldsymbol{H}^{(l)}=\begin{pmatrix}1.&1.&1.&0.\\1.&1.&1.&0.\\1.&1.&1.&1.\\0.&0.&1.&1.\end{pmatrix}*\begin{pmatrix}1.&0.&0.\\0.&1.&0.\\0.&0.&1.\\0.&1.&1.\end{pmatrix}=\begin{pmatrix}1.&1+1.&1.\\1.&1.&1.\\1.&1+1.&1+1.\\0.&1.&1+1.\end{pmatrix}\)

上式表示每个节点向量要同时考虑自身节点和它相邻节点的信息。\(\tilde{D}\)是度矩阵，表示的是每个节点的度数。例如，图1中的一号和二号节点，考虑其自连接，则度数等于3；同理，三号节点度数为4，而四号节点度数为2，因此得到下述度矩阵。

\(\tilde{\boldsymbol{D}}=\begin{pmatrix}3.&0.&0.&0.\\0.&3.&0.&0.\\0.&0.&4.&0.\\0.&0.&0.&2.\end{pmatrix}\)

\(\tilde{D}^{-1}\)表示将度矩阵中的元素取倒数，得到：

\(\tilde{\boldsymbol{D}}^{-1}=\begin{pmatrix}1/3.&0.&0.&0.\\0.&1/3.&0.&0.\\0.&0.&1/4.&0.\\0.&0.&0.&1/2.\end{pmatrix}\)

\(\tilde{D}^{-1}(\tilde{A}H^{(l)})\)相当于对\(\tilde{A}H^{(l)}\)结果的行进行归一化操作，它有助于避免由于图中节点度的不均匀分布引起的梯度爆炸或消失问题。确保了所有节点的特征贡献在聚合时被适当地缩放，从而提高了学习的稳定性和效果。公式计算如下：

\(\tilde{\boldsymbol{D}}^{-1(}\tilde{A}\boldsymbol{H}^{(l)})=\begin{pmatrix}1/3.&0.&0.&0.\\0.&1/3.&0.&0.\\0.&0.&1/4.&0.\\0.&0.&0.&1/2.\end{pmatrix}*\begin{pmatrix}1.&1+1.&1.\\1.&1.&1.\\1.&1+1.&1+1.\\0.&1.&1+1.\end{pmatrix}=\begin{pmatrix}1/3*1.&1/3*(1+1).&1/3*1.\\1/3*1.&1/3*1.&1/3*1.\\1/4*1.&1/4*(1+1).&1/4*(1+1).\\1/2*0.&1/2*1.&1/4*(1+1).\end{pmatrix}\)

同理，\((\tilde{A}H^{(l)})\tilde{D}^{-1}\)相当于对\(\tilde{A}H^{(l)}\)结果的列做归一化。最后，式\(H^{l+1}=\sigma(\tilde{D}^{-\frac12}\tilde{AD}^{-\frac12}H(l)W(l))\)中左乘和右乘的矩阵使用的是\(\tilde{D}^{-\frac12}\)而不是\(\boldsymbol{\tilde{D}}^{-1}\)的原因是：当对行列元素各做一次归一化后，相当于对节点向量的每个元素都做了两次归一化，也就是多做了一次，因此这里使用做归一化的矩阵的是\(\tilde{D}^{-\frac12}\)。最终，图卷积神经网络的计算公式则为：

\(\boldsymbol{H}^{l+1}=\sigma(\tilde{\boldsymbol{D}}^{-\frac12}\tilde{\boldsymbol{AD}}^{-\frac12}\boldsymbol{H}(l)\boldsymbol{W}(l))\)

尽管图卷积网络（GCN）和卷积神经网络（CNN）都是“卷积”概念的扩展，但它们在处理数据的方式和结构上有很大的不同。在CNN中，卷积是定义在规则的网格数据（如图像）上的。这种卷积操作通常涉及到固定大小的滤波器（卷积核）在输入数据上滑动，提取局部特征。在GCN中，卷积操作是在图结构上定义的，这意味着它需要考虑图的拓扑结构。GCN中的“卷积”是通过聚合一个节点及其邻居的特征来实现的，这种聚合考虑了图的连接性而非空间的临近性。更重要的是在聚合邻居节点信息时，引入了自身节点的信息，并通过节点的度对聚合的特征进行归一化。这种归一化处理有助于避免节点度的大小对特征聚合造成过大的影响，使得特征表示更加平滑和稳定。总结来说，尽管GCN中的“卷积”与传统的CNN在技术细节上有所不同，但其核心思想都是利用局部连接结构信息进行特征学习和聚合，这也是为什么将这种操作称为“卷积”的原因。

另外，GCN更适用于Transductive任务，因为GCN在更新节点向量时，利用到了基于整个邻接矩阵信息的拉普拉斯矩阵\((\tilde{D}^{-\frac{1}{2}}\tilde{AD}^{-\frac{1}{2}})\)，从这种意义上讲它聚合邻居特征的时候，训练出来的权重\(W\)是考虑了整个图结构的，如果图结构改变，那么就不再适用。因此GCN在处理Inductive任务时表现不佳。