LEFTNet
1、三种图同构问题
图同构问题是图论中的一个基本问题,它要求确定两个图是否在结构上完全相同。具体来说,这意味着存在一种顶点间的一对一映射,使得两个图中的顶点相互连接的方式完全一致。如果这样的映射存在,这两个图被认为是同构的。图神经网络是一种专为处理图结构数据设计的神经网络架构,它能够通过节点的特征信息和连接模式来学习图的表示。一个优秀的几何GNN模型可以有效地学习和提取节点和边的特征。这种学习方式使得GNN能够捕捉到图的局部和全局结构特征,这是判断图同构问题时的关键。简单说,对于图同构的识别能力是衡量GNN模型表征能力的重要方面。
LEFTNet中,定义了三种图同构结构:
(1)树同构:任意邻接的两原子间的距离一致。
(2)三角同构:任意邻接的三原子构成的三角形一致。
(3)子图同构:任意两个三角形的相对位置保持一致。
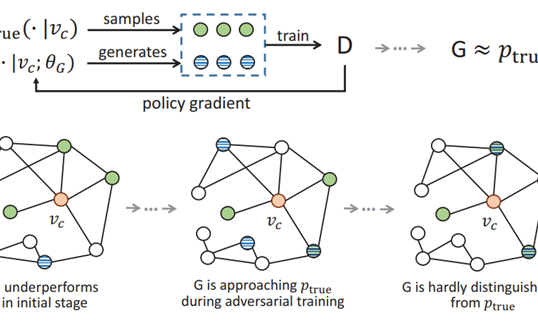
具体示例如图1所示:
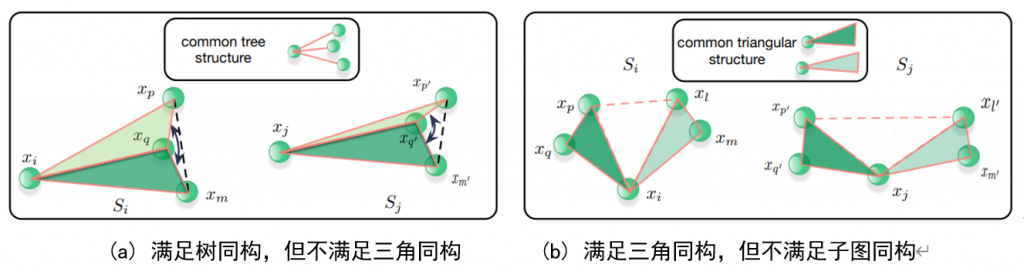
在图1(a)中,展示了一种满足树同构,但不满足三角同构的情况。三角同构不仅仅是距离上的相似,还包括了角度和方向的一致性。在图1(b)中,展示了一种满足三角同构,但不满足子图同构的情况,而LEFTNet的模型设计方向是让模型对这三种情况都有表征能力。
首先,为了满足树同构的要求,作者认为:只要正确抽取原子间距离即可,所有的几何GNN,无论是等变性质的还是不变性质的几乎均满足。
其次,为了满足三角同构的要求,作者认为:三角同构本质上是局域完备性问题。通过设计一个合理的局域正交坐标系,让此局域坐标有能力可以表征局部空间范围内所有的几何向量。同时还需要满足等变要求,通过将原坐标映射到局域坐标,即可满足局域完备性的要求。这里,LEFTNet的模型直接采用ClofNet中提出的局域坐标系。
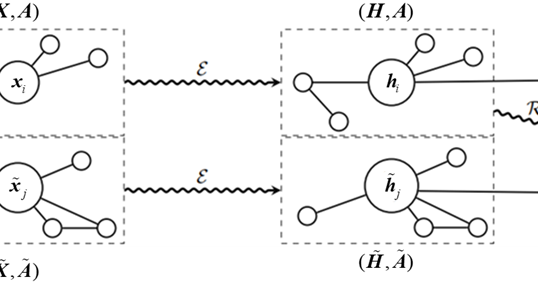
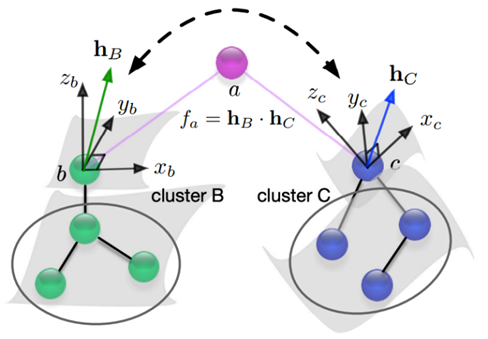
最后,为了满足子图同构的要求,模型需要将局域完备性扩展到全域完备性,且这个过程是信息无损的。不幸的是,图结构中不同的节点建立的局域坐标系是不同的。不同局域坐标系相对位置不一样,换句话说,对不同局域坐标系对局部范围内点位置信息的建模角度不同,这导致局域信息汇聚过程中遭受信息损失,如图2所示。

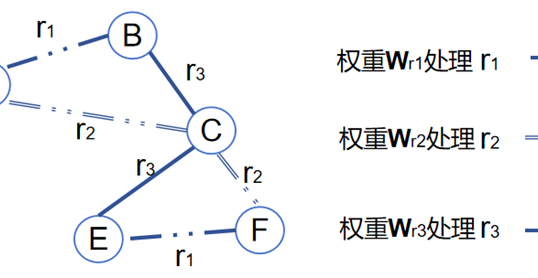
如图2所示,点b和点c分别建立了局域坐标系,在这两个局域坐标系下,cluster(团簇)b和cluster c进行了有效映射。但由于局域坐标下的不同,b处的局域信息和c处的局域信息融合时会存在问题。类比理解可以将cluster b和cluster c看作喜结连理的一对夫妻的原生家庭,由于两个原生家庭所在的生活环境不同,直接交流起来难免存在矛盾。这时候怎么办呢?当然是找夫妻的家人或朋友做中间调理人呀!同理,可以通过节点b和c二者共同的邻居们 a(可能不止一个),两个局域坐标系的信息交互与融合便会更加的有效。下面给出相关概念的具体定义:
令\(S_{i}\)表示与上图节点\(\mathrm{b}\)关联的局域\(\text{clusterb}\),这个局域包含节点\(\mathrm{b}\)的所有一跳邻居(1-hop neighbors)。类似的,定义令\(S_{j}\)表示与上图节点\(\mathrm{c}\)关联的局域\(\text{clusterc}\)。这个局域包含节点\(\mathrm{c}\)的所有一跳邻居(1-hop neighbors)。此时可以定义\(S_{i-j}\),表示节点\(\mathrm{b}\)和节点\(\mathrm{c}\)之间的共享或相互的3D子结构。具体来说,是通过取两个局域\(\text{clusterb}\)和\(\text{clusterc}\)的交集来定义的,这意味着\(S_{i-j}\)包括了所有同时是节点\(\mathrm{b}\)和节点\(\mathrm{c}\)的一跳邻居的节点,以及连接这些节点的边。
2、LSE模块提取局域信息
定义LEFNet的输入数据为几何图数据,其具有等变位置信息\(X=\left(x_{1},\ldots,x_{n}\right)\in\mathbb{R}^{n\times3}\)、不变节点特征\(h_i\in\mathbb{R}^d\)、不变相对距离\(d_{ij}\in R^{1}\)、等变边特征\(e_{ij}\in\mathbb{R}^c\)。LEFNet模型中使用LSE模块提取局域信息的步骤如下:
步骤1:与ClofNet类似,将位置信息中心化:\(X\leftarrow X-\mathrm{CoM}(X)\)。这通常意味着会从每个位置向量中减去所有位置向量的平均值,以确保模型对平移保持不变。
步骤2:通过ClofNet中提出的局域正则坐标系,计算图中每个节点\(\mathrm{i}\)与其对应的每个邻居节点\(\mathrm{j}\)之间形成的等变局域正交表示\(\mathcal{F}_{ij}\)。具体来说,考虑节点\(\mathrm{i}\)和它的一个邻居节点\(\mathrm{j}\),它们的位置分别是\(x_{i}\)和\(x_{j}\)。定义与\(x_{i}\)和\(x_{j}\)相关的正交等变框架\(F_{ij}\)如下:
\(F_{ij}:=\left(\frac{x_i-x_j}{\left\|x_i-x_j\right\|},\frac{x_i\times x_j}{\left\|x_i\times x_j\right\|},\frac{\left(x_i-x_j\right)\times\left(x_i\times x_j\right)}{\left\|\left(x_i-x_j\right)\times\left(x_i\times x_j\right)\right\|}\right)\)
类似的,计算图中每个节点\(\mathrm{i}\)的等变局域正交表示\(\mathcal{F}_{i}\)。具体来说,考虑具有三维位置\(x_{i}\)的节点\(\mathrm{i}\),并令\(\overline{x}i:=\frac{1}{N}\sum{x_j\in N(x_i)}x_j\)为\(x_{i}\)的1跳邻域内所有节点的质心。定义与\(x_{i}\)相关的正交等变框架\(\mathcal{F}_{i}\)如下:
\(F_i:=\left(\frac{x_i-\overline{x}_i}{\left\|x_i-\overline{x}_i\right\|},\frac{\overline{x}_i\times x_i}{\left\|\overline{x}_i\times x_i\right\|},\frac{\left(x_i-\overline{x}_i\right)\times\left(\overline{x}_i\times x_i\right)}{\left\|\left(x_i-\overline{x}_i\right)\times\left(\overline{x}_i\times x_i\right)\right\|}\right)\)
步骤3:获取节点\(\mathrm{i}\)的1-hop邻域和节点 的1-hop的共享3D区域\(S_{i-j}\),并通过\(\mathcal{F}_{ij}\)进行\(S_{i-j}\)局部信息的标量化:
\(t_{ij}=\left\{\mathrm{Scalarize}\left(S_{i-j},F_{ij}\right)\right\}\)
标量化的具体方式与clofNet中提出的一样,将代表\(S_{i-j}\)局部信息的几何向量投影到\(\mathcal{F}_{ij}\)的基组上,通过内积获得相应的系数即可得到结果\(t_{ij}\),\(t_{ij}\)是用标量形式存储的几何向量信息。
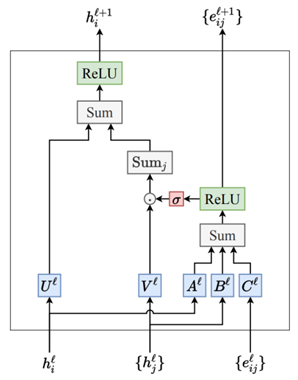
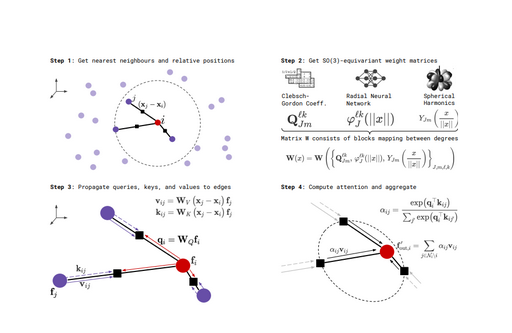
步骤4:对\(t_{ij}\)进行最后的特征编码得到区域\(S_{i-j}\)的几何空间特征表示,具体来说,\(S_{i-j}\)会先经过径向模型RBF的处理,得到相对距离信息,将此信息与几何向量信息\(t_{ij}\)点乘进行标量信息和向量信息的交互。其结果将使用神经网络层MLP进行最后的学习,计算出\(S_{i-j}\)最后的几何空间特征表示\(A_{ij}\)。上述LSE模块提取局域信息的计算流程可用图3进行表示。
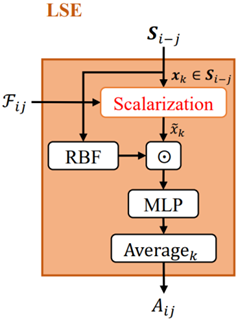
3、EMP模块进行图的消息传递
EMP被定义为Equivariant Massage Passin,当通过LSE模块得到\(S_{i-j}\)的几何空间特征表示\(A_{ij}\)之后,就可以进行节点\(\mathrm{i}\)和其邻居\(\mathrm{j}\)之间的等变性消息传递了,其公式表示为:
\(\boldsymbol{m}_{ij}=\phi_m^1\left(h_i,A_{ij}\odot h_j,d_{ij}\right)+\phi_m^2\left(h_i,A_{ij}\odot h_j,d_{ij}\right)\cdotp\boldsymbol{e}_{ij}+\phi_m^3\left(h_i,A_{ij}\odot h_j,d_{ij}\right)\cdotp\mathcal{F}_{ij}\)
其中:
(1)\(m_{ij}\)是从节点\(\mathrm{j}\)到节点\(\mathrm{i}\)的消息。
(2)\(h_{i}\)和\(h_{j}\)分别是节点\(\mathrm{i}\)和节点\(\mathrm{j}\)的特征向量。
(3)\(A_{ij}\)是通过LSE模块获得的,表示节点\(\mathrm{i}\)和节点\(\mathrm{j}\)之间的局部几何空间特征。
(4)\(\odot\)表示哈达玛积(元素级的乘法),在这里用于将空间关系\(A_{ij}\)直接与节点\(\mathrm{j}\)的特征\(h_{j}\)结合起来,以获得节点\(\mathrm{j}\)与几何空间相关的特征。
(5)\(d_{ij}\)是节点\(\mathrm{i}\)和\(\mathrm{j}\)之间的不变距离,它提供了两个节点之间距离关系的附加信息。
(6)\(e_{ij}\)是连接节点\(\mathrm{i}\)和\(\mathrm{j}\)的边的向量特征。
(7)\(\mathcal{F}_{ij}\)是边\((i,j)\)的等变框架。
(8)\(\phi_m^1,\phi_m^2,\phi_m^3\)是可学习的函数,它们通过参数化的方式处理输入的特征,生成最终消息。这些函数是由神经网络层如全连接层实现的。
上述公式的理解可以分成三个部分来解释:
1、特征组合:
将节点\(\mathrm{i}\)和节点\(\mathrm{j}\)的特征\(h_{i}\)和\(h_{j}\)与局部结构表示\(A_{ij}\)进行组合。符号\(\odot\)表示特征之间的逐元素乘积操作,用于结合节点特征和局部结构信息:
\(\phi_m^1(h_i,A_{ij}\odot h_j,d_{ij})\)
其中\(\phi_m^1\)是一个神经网络,用于处理结合后的特征。\(d_{ij}\)是节点\(\mathrm{i}\)和节点\(\mathrm{j}\)之间的距离信息,作为额外的输入特征。
2、方向信息处理:
使用边的方向信息\(\boldsymbol{e}_{ij}\)来增强特征表示,通过函数\(\phi_{m}^{2}\)对组合特征和方向信息进行处理:
\(\phi_{m}^{2}(h_{i},A_{ij}\odot h_{j},d_{ij})\cdot\boldsymbol{e}_{ij}\)
方向信息\(\boldsymbol{e}_{ij}\)与特征的点积操作捕捉了节点之间的相对方向信息。
3、框架信息处理:
处理节点\(\mathrm{i}\)的框架信息\(\mathcal{F}_i\),并结合到特征表示中,通过函数\(\phi_m^3\)对组合特征和框架信息进行处理:
\(\phi_m^3(h_i,A_{ij}\odot h_j,d_{ij})\cdot\mathcal{F}_i\)
这一步确保了节点特征中包含框架转移信息,使得表示更丰富。
值得注意的是,这个消息传递机制是等变的,因为它将空间结构信息\(A_{ij}\)和等变框架\(\mathcal{F}_{ij}\)结合到消息传递过程中。等变框架\(\mathcal{F}_{ij}\)保证了消息的方向与图形的几何方向一致,而\(A_{ij}\)保持了节点间关系的几何一致性。
4、FTE模型进行图的消息更新
在使用EMP模块进行图的消息传递之后,接下来使用FTE模块进行图消息的更新,整个消息交互模块如图4所示。
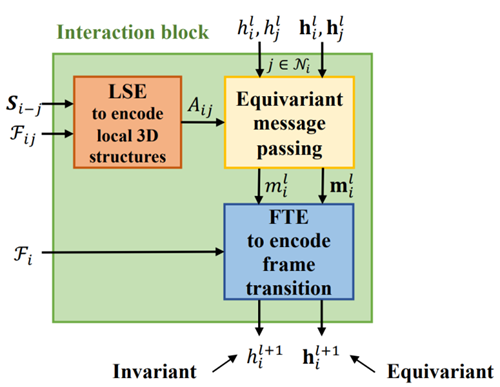
在FTE模块中,首先进行消息聚合:\(m_i=\sum_{j\in N(i)}m_{ij}\),这个操作表明每个节点\(\mathrm{i}\)的消息\(m_{i}\)是其所有邻居\(\mathrm{j}\)的消息\(m_{ij}\)的总和,接下来的操作如图5所示。
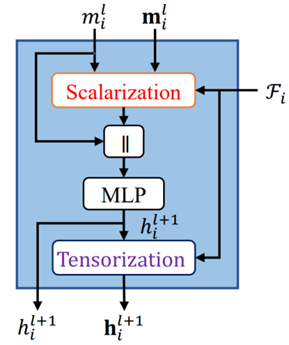
通过局域坐标系\(\mathcal{F}_{i}\)将节点特征中的位置信息进行标量化:\(t_i=Scalarize(m_i,\mathcal{F}_i)\),标量化是将向量信息(在这里是消息\(m_{i}\))投影到一组基\(\begin{pmatrix}\mathcal{F}_i\end{pmatrix}\)上,产生一组标量值。标量化的结果与节点\(\mathrm{i}\)的特征进行拼接,送入MLP中进行学习,映射得到更新后的节点\(\mathrm{i}\)的特征\(h_{i}^{l+1}\),\(h_{i}^{l+1}\)不仅仅反映了节点\(\mathrm{i}\)自己的信息,因为标量化的参与,还可以包含其邻居节点相对于\(\mathrm{i}\)的几何关系。
接下来更新等变向量特征\(\boldsymbol{h}_{i}^{l+1}\),\(\boldsymbol{h}_i^{l+1}=\mathrm{Tensorize}\left(h_i^{l+1},\mathcal{F}_i\right)\),通过标量化的逆操作 Tensorize,将更新的节点特征\(h_{i}\)转换回向量形式。函数Tensorize 利用节点\(\mathrm{i}\)的局部参照框架\(\mathcal{F}_{i}\),将标量特征\(h_{i}\)转换回一个向量或者张量,这个向量或者张量能够反映出图数据在三维空间中的方向性和位置。
通过上述操作,LEFTNet的消息传递模块最终获得了一个节点特征表示\(h_i^{l+1}\),以及一个向量表示\(\boldsymbol{h}_{i}^{l+1}\)。它们既蕴含了节点在其邻域内的丰富信息,又能够响应外部的空间变换,确保网络输出的一致性和适用性,这对于建立鲁棒的图处理模型至关重要,LEFTNet整体的模型结构如图6所示。
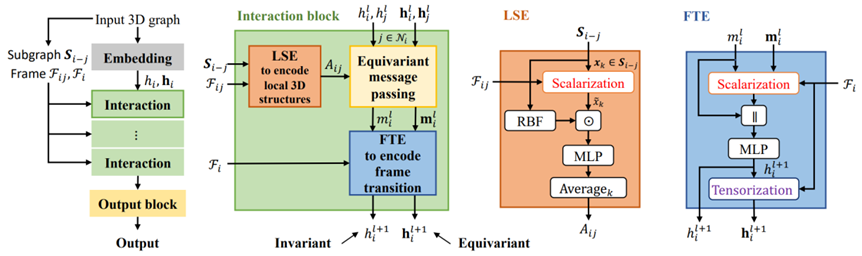
作者
arwin.yu.98@gmail.com