Graph Attention Network（GAT）

接下来介绍图注意力网络GAT，GAT可以有两种运算方式，一种被称为全局注意力（Global Graph Attention），顾名思义，就是每一个顶点都对于图上任意顶点都进行Attention运算。这样做的优点是完全不依赖于图的结构，即不依赖图的邻接矩阵，对于Inductive任务无压力。缺点也很明显：首先，丢掉了图结构的特征。其次，当图数据规模很大的时候，运算面临着高昂的成本。第二种被称为掩码图注意力机制（Mask Graph Attention），每个节点的Attention计算仅限于其邻接节点（即邻接矩阵所定义的直接连接）。这样做保留了图的结构特性，并利用了局部邻域信息。与全局注意力相比，掩码图注意力机制大大降低了计算成本，因为每个节点只与其直接邻居进行交互，而不是图中的所有节点。这种方式有效地利用了图的拓扑结构，可以捕捉到节点之间的局部关系，这对于许多图数据分析任务是非常有价值的。值得注意的是，虽然在掩码图注意力机制的GAT中用到了邻接矩阵，但是并不像GCN一样是利用全部的邻接矩阵信息，而是仅利用邻接矩阵查询某节点的邻居是谁。因此可以来处理Inductive任务。换句话说，GAT中节点可以通过注意力权重动态地选择其信息的重要来源，即它的邻居。这些权重是由模型通过学习自动确定的，并不依赖于预先定义的结构。这一点区别于GCN，后者使用的是固定的邻接矩阵加自环的归一化形式来确定节点之间信息传递的权重。

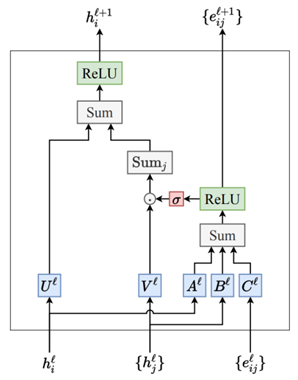
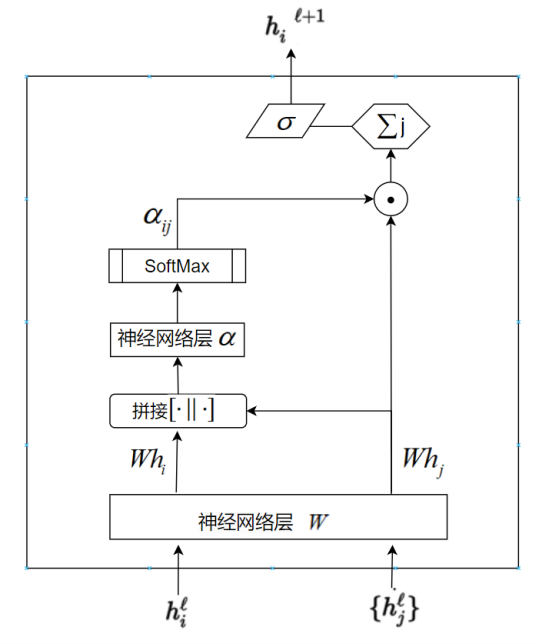
接下来主要讲解GAT中的 Attention机制。类似于Transformer中的注意力机制，GAT的计算也分为两步：计算注意力系数（Attention Coefficient）和加权求和（Aggregate）进行特征重要程度的重分配。对于顶点i，逐个计算它的邻居们（\(j\in N_{i}\)）和它的注意力系数\(e_{ij}=\alpha([Wh_i\parallel Wh_j]),j\in\mathcal{N}_i\)，具体流程如图1所示。

在图1中\(h_{i}^{l}\)是节点i的特征向量，\({h_j^l}\)是的节点i所有邻居的特征向量的集合，W是一个共享参数，通过一个单层的神经网络层来实现。\([\cdot||\cdot]\)代表对节点i,j经过神经网络层W变换后的特征进行拼接操作（Concat）。最后通过\(\alpha\)把拼接后的高维特征映射到一个实数上，也是通过一个单层的神经网络层来实现。显然学习节点i,j之间的相关性系数，就是通过可学习的神经网络层的参数W和\(\alpha\)映射完成的。有了相关系数，再对其进行Softmax归一化操作即可得到注意力系数\(\alpha_{ij}\)。至于加权求和的实现也很简单，根据计算好的注意力系数，把特征加权求和聚合（Aggregate）一下。即：

\(h_i'=\sigma(\sum_{j\in\mathcal{N}_i}\alpha_{ij}Wh_j)\)

\(h_i^{\prime}\)就是GAT 输出的对于每个节点i的新特征，这个新特征的向量表示融合了邻域信息，\(\sigma(\cdot)\)是激活函数。最后，与Transformer一样，GAT也可以用多头注意力机制来进化增强：

\(h'_i(K)=\|_{k=1}^K\sigma(\sum_{j\in\mathcal{N}_i}\alpha_{ij}^kW^kh_j)\)

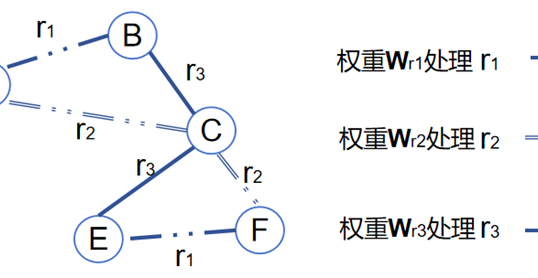
其中K是注意力机制的头数，每个头都会维护更新自己的参数，计算得到自己的结果，\(||_{k-1}^K\)表示将所有头的计算结果进行拼接（Concat）得到最后更新好的新节点向量。多头注意力机制也可以理解成用了集成学习的方法，就像卷积中，也要靠大量的卷积核才能有比较好的特征提取效果一样。最后通过一个示例来复习一下GAT的计算过程，图数据如图2所示。

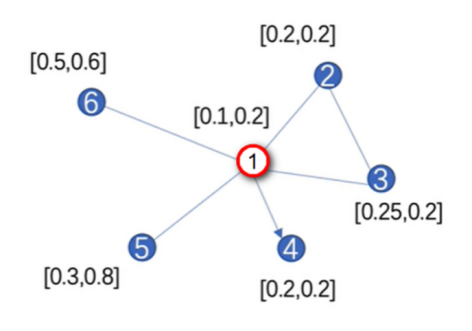
计算注意力系数的两个神经网络层的参数分别是W和\(\alpha\)，假设其初始化的值为W=[1,1],\(\alpha\)=[1,1,1,1]。注意，这些参数都是可学习的，随着网络的训练而更新。首先，计算注意力系数\(e_{ij}=\alpha(Wh_i,Wh_j)\)，以节点1为例，与其它节点的相关性系数为：

\(\begin{aligned}
&e_{12}=\alpha\cdot[0.1,0.2,0.2,0.2]=0.7 \\
&e_{13}=\alpha\cdot[0.1,0.2,0.25,0.2]=0.75 \\
&e_{14}=0 \\
&e_{15}=\alpha\cdot[0.1,0.2,0.3,0.8]=1.4 \\
&e_{16}=\alpha\cdot[0.1,0.2,0.5,0.6]=1.4
\end{aligned}\)

\(e_{14}\)由于单向性，即节点1指向4，因此在计算更新节点1的信息时，节点4的信息不会传递给节点1，因此其相关性\(e_{14}\)为零。然后通过Softmax公式计算得到相关性系数：

\(\alpha_{ij}=\frac{\exp(LeakyReLU(\vec{a}^T[W\vec{h}_i\parallel W\vec{h}_j]))}{\sum_{k\in\mathcal{N}_i}\exp(LeakyReLU(\vec{a}^T[W\vec{h}_i\parallel W\vec{h}_k]))}\)

例如\(\alpha_{12}\)：

\(\alpha_{{_{12}}}=\frac{\exp(\mathrm{LeakyReLU}(e_{{_{12}}}))}{\exp(\mathrm{LeakyReLU}(e_{{_{12}}}))+\exp(\mathrm{LeakyReLU}(e_{{_{13}}}))+\ldots+\exp(\mathrm{LeakyReLU}(e_{{_{16}}}))}\)

然后通过加权求和对某节点的邻居做重要程度的重分配，即：

\(\vec{h_i^{\prime}}=\sigma(\sum_{j\in N_i}\alpha_{ij}W\vec{h_j})\)

以节点1为例：

\(\vec{h}_1^{\prime T}=\sigma\left(\alpha_{12}\cdot W\cdot\vec{h}_2\right)+\sigma\left(\alpha_{13}\cdot W\cdot\vec{h}_3\right)+\sigma\left(\alpha_{15}\cdot W\cdot\vec{h}_5\right)+\sigma\left(\alpha_{16}\cdot W\cdot\vec{h}_6\right)\)

本质上而言：GCN与GAT都是将邻居节点的特征聚合到中心节点上，利用图数据上的局部连接性学习新的节点特征表达。不同的是GCN利用了拉普拉斯矩阵（\(\tilde{D}^{-\frac12}\tilde{AD}^{-\frac12}\) ​）计算得到聚合过程中每个节点的权重，这个过程是一个预定义的数学方法，不涉及可学习参数。而GAT利用attention系数（\(\alpha_{ij}\)），这其中设计两个神经网络层的可学习参数W和\(\alpha\ )。

最后探讨一下为什么GAT适用于Inductive任务，因为GAT聚合邻居特征的时候仅仅只需要考虑邻居特征，训练出来的参数W和\(\alpha\)是对邻居特征的线性变换参数矩阵，这个参数矩阵针对每一个节点的每一个邻居都是一样的，也就是所谓的共享权重参数。这些仅与节点特征相关，没有直接用到邻接矩阵进行计算。所以测试任务中改变图的结构，对于GAT影响并不大，只需要更新节点的邻居集合\(N_{i}\)，然后用GAT模型重新计算注意力系数和节点的表示即可。这里的重新计算并不是指重新训练模型，只需要用训练好的权重参数对更新后的邻居集合进行前向传播。这是因为在前向传播过程中，注意力系数是基于节点和邻居的特征动态计算的，而不是静态地依赖于原始图的结构。因此，即使图的结构发生了变化，这些计算仍然是有效的。且在GAT的训练中，由于权重参数是在不同节点间共享的，并且在聚合过程中主要依赖于节点的特征而非图的全局结构，所以这些权重能够根据节点间的特征进行某些属性的预测，并不强依赖于图的结构，使得模型能够很好地泛化到新的、未见过的图结构上。