线性代数

 Deep Learning Math
Deep Learning Math
线性代数(Linear Algebra Tutorial)
线性代数在深度学习中占据核心地位。线性方程组和增广矩阵用于描述和解决系统中的多变量关系。向量操作,如向量数乘、加法和线性组合,构成了深度学习中数据和权重的基本表示。向量空间和线性相关/无关的概念帮助我们理解数据的结构和维度。点积和外积在计算相似度和生成新向量时非常重要,而正交与基组则用于简化计算和减少维度。
矩阵运算,如矩阵乘法、哈达玛积和克罗内克积,是深度学习中张量操作的基础。初等矩阵和可逆矩阵的概念用于优化和求解模型参数。行列式和矩阵的秩帮助确定系统的解和矩阵的属性,而矩阵的特征值与特征向量则用于理解数据的变换和降维。通过这些线性代数工具,深度学习模型能够高效处理和表示大量数据,实现复杂计算和模型优化。
 Agenda
Agenda
- 线性方程组(Linear Equations)
- 增广矩阵
- 向量(Vector)
- 向量数乘
- 向量加法
- 向量线性组合
- 向量空间
- 线性相关/无关
- 点积/内积
- 外积
- 叉积
- 正交与基组
- 矩阵(Matrix)
- 矩阵乘法
- 哈达玛积
- 克罗内克积
- 初等矩阵
- 可逆矩阵
- 行列式
- 矩阵的秩
- 矩阵的特征值与特征向量
 Linear Algebra
Linear Algebra
线性代数的难点在于其涉及多种表示系统,包括方程组表示、向量表示和矩阵表示等。理解和掌握这些不同表示方法之间的关系与转换是至关重要的,因为它们在解决实际问题时提供了不同的视角和工具。例如,
-
方程组表示通常用于描述和求解系统的线性关系
-
向量表示则强调几何和代数结构
-
矩阵表示提供了处理和计算多变量线性系统的强大框架。
全面理解这些表示方法及其相互转换,不仅有助于深化对线性代数理论的理解,也能够提高在实际应用中灵活运用这些工具解决复杂问题的能力。
 Systems of Linear Equations:
Systems of Linear Equations:
先从线性方程组开始讲起,线性方程组是涉及同一组变量的方程的集合。线性方程组的一般形式如下所示:
$$\begin{cases}a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1\\a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2\\
\vdots \\
a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n=b_m\end{cases}$$
其中 $a_{i j}$ 表示 $i$ 行 $j$ 列的系数, $x_n$ 表示变量/未知数, $b_m$ 表示常数
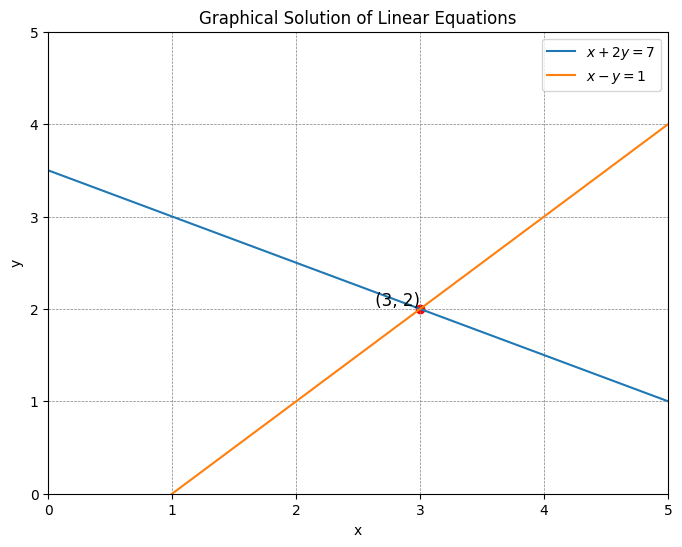
举个例子, 现在有方程组如下:
$$
\begin{cases}
x + 2y = 7 \\
x - y = 1
\end{cases}
$$
每个方程都只有两个未知数, 这样的方程就是二维空间中的一条直线。而求含有两个未知数的两个方程组成的方程组的解, 等价于求两条直线的交点。很容易求出以上线性方程组的解为 $x=3, y=2$, 图形结果如下所示。
import numpy as np
import matplotlib.pyplot as plt
# 定义方程
def equation1(x):
return (7 - x) / 2
def equation2(x):
return x - 1
# 定义x范围
x = np.linspace(0, 5, 400)
# 计算y值
y1 = equation1(x)
y2 = equation2(x)
# 绘制图形
plt.figure(figsize=(8, 6))
plt.plot(x, y1, label=r'$x + 2y = 7$')
plt.plot(x, y2, label=r'$x - y = 1$')
# 标记交点
plt.scatter(3, 2, color='red')
plt.text(3, 2, ' (3, 2)', fontsize=12, verticalalignment='bottom', horizontalalignment='right')
# 设置图形属性
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.legend()
plt.title('Graphical Solution of Linear Equations')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(0, 5)
plt.ylim(0, 5)
plt.show()
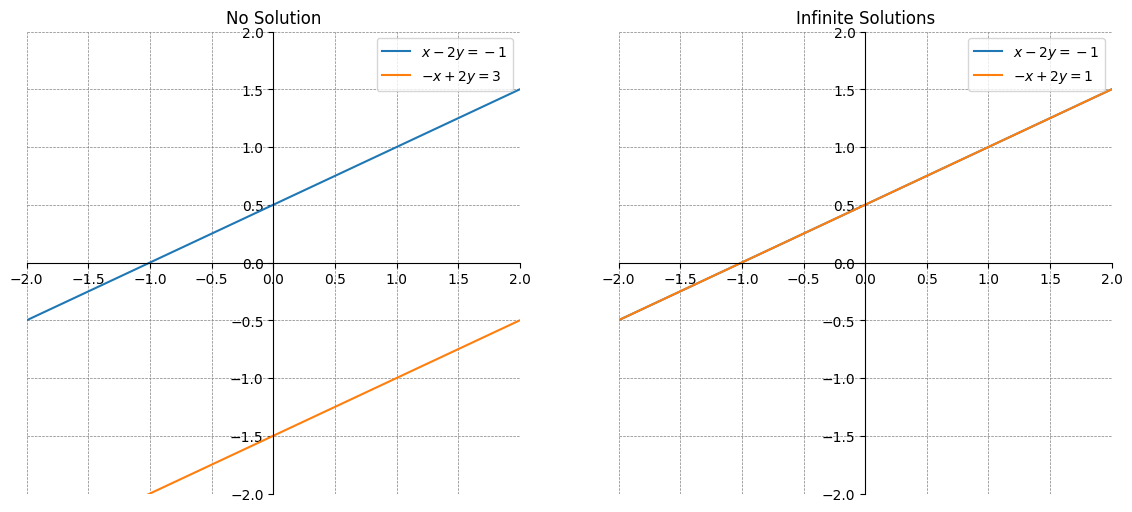
此时,方程组存在一个唯一解。当然,两条直线并不一定交于一点,它们可能平行,也可能重合,重合的两条直线上的每个点都是交点。考虑下面两个方程组:
$$
\begin{cases} { l }
{ x - 2 y = - 1 } \\
{ - x + 2 y = 3 }
\end{cases}
\\
\begin{cases}{l}
x-2 y=-1 \\
-x+2 y=1
\end{cases}
$$
其中第一个方程组中的两条直线平行,没有交点,即方程组无解;第二个方程组中的两条直线重合,有无数交点,即方程组有无穷多解。
import numpy as np
import matplotlib.pyplot as plt
# 定义方程组的方程
def equation1a(x):
return (x + 1) / 2
def equation1b(x):
return (x - 3) / 2
def equation2a(x):
return (x + 1) / 2
def equation2b(x):
return (x + 1) / 2
# 定义x范围
x = np.linspace(-2, 2, 400)
# 计算y值
y1a = equation1a(x)
y1b = equation1b(x)
y2a = equation2a(x)
y2b = equation2b(x)
# 绘制图形
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# 第一个方程组
ax1.plot(x, y1a, label=r'$x - 2y = -1$')
ax1.plot(x, y1b, label=r'$-x + 2y = 3$')
ax1.set_title('No Solution')
ax1.axhline(0, color='black',linewidth=0.5)
ax1.axvline(0, color='black',linewidth=0.5)
ax1.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
ax1.legend()
ax1.set_xlim(-2, 2)
ax1.set_ylim(-2, 2)
ax1.spines['left'].set_position('zero')
ax1.spines['bottom'].set_position('zero')
ax1.spines['right'].set_color('none')
ax1.spines['top'].set_color('none')
ax1.xaxis.set_ticks_position('bottom')
ax1.yaxis.set_ticks_position('left')
# 第二个方程组
ax2.plot(x, y2a, label=r'$x - 2y = -1$')
ax2.plot(x, y2b, label=r'$-x + 2y = 1$')
ax2.set_title('Infinite Solutions')
ax2.axhline(0, color='black',linewidth=0.5)
ax2.axvline(0, color='black',linewidth=0.5)
ax2.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
ax2.legend()
ax2.set_xlim(-2, 2)
ax2.set_ylim(-2, 2)
ax2.spines['left'].set_position('zero')
ax2.spines['bottom'].set_position('zero')
ax2.spines['right'].set_color('none')
ax2.spines['top'].set_color('none')
ax2.xaxis.set_ticks_position('bottom')
ax2.yaxis.set_ticks_position('left')
plt.show()
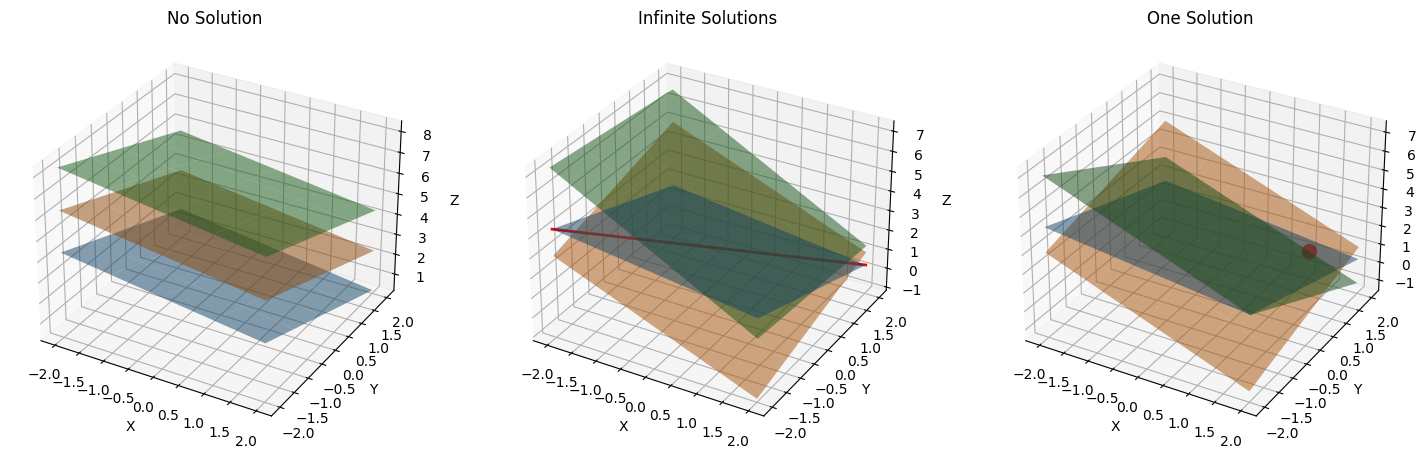
通过上面的例子,可以总结一个重要的结论:线性方程组的解只有三种情况:一个解、无穷解和无解。
现在把方程扩展到三个未知数的线性方程组,这样每个方程将确定三维空间中的一个平面。
现在想象一下三个这样的平面在三维空间中的分布会有几种情况?其实也是上述的三种情况:
- 当三个平面相互平行时,无解。
- 当三个平面相交于一条线时,无穷解。
- 当三个平面相较于一点时,只有一个解。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 定义三个平面
def plane1(x, y):
return (7 - x - 2*y) / 3
def plane2(x, y):
return (4 - 2*x + y) / 2
def plane3(x, y):
return 3 - x - y
# 定义x, y范围
x = np.linspace(-2, 2, 400)
y = np.linspace(-2, 2, 400)
X, Y = np.meshgrid(x, y)
# 计算z值
Z1 = plane1(X, Y)
Z2 = plane2(X, Y)
Z3 = plane3(X, Y)
# 创建图形对象
fig = plt.figure(figsize=(18, 6))
# 第一种情况:无解
ax1 = fig.add_subplot(131, projection='3d')
ax1.plot_surface(X, Y, Z1, alpha=0.5, rstride=100, cstride=100)
ax1.plot_surface(X, Y, Z1 + 2, alpha=0.5, rstride=100, cstride=100)
ax1.plot_surface(X, Y, Z1 + 4, alpha=0.5, rstride=100, cstride=100)
ax1.set_title('No Solution')
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')
# 第二种情况:无穷解
ax2 = fig.add_subplot(132, projection='3d')
ax2.plot_surface(X, Y, Z1, alpha=0.5, rstride=100, cstride=100)
ax2.plot_surface(X, Y, Z2, alpha=0.5, rstride=100, cstride=100)
ax2.plot_surface(X, Y, Z1 + Z2, alpha=0.5, rstride=100, cstride=100)
# 添加交线
intersection_line_x = np.linspace(-2, 2, 100)
intersection_line_y = intersection_line_x
intersection_line_z = plane1(intersection_line_x, intersection_line_y)
ax2.plot(intersection_line_x, intersection_line_y, intersection_line_z, color='red', linewidth=2)
ax2.set_title('Infinite Solutions')
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.set_zlabel('Z')
# 第三种情况:一个解
ax3 = fig.add_subplot(133, projection='3d')
ax3.plot_surface(X, Y, Z1, alpha=0.5, rstride=100, cstride=100)
ax3.plot_surface(X, Y, Z2, alpha=0.5, rstride=100, cstride=100)
ax3.plot_surface(X, Y, Z3, alpha=0.5, rstride=100, cstride=100)
# 添加交点
intersection_point = np.array([1, 2, 0]) # 示例交点
ax3.scatter(intersection_point[0], intersection_point[1], intersection_point[2], color='red', s=100)
ax3.set_title('One Solution')
ax3.set_xlabel('X')
ax3.set_ylabel('Y')
ax3.set_zlabel('Z')
plt.show()
再来看线性方程组的一般公式:
$$
\begin{cases}
a_{11} x_1+a_{12} x_2+\cdots+a_{1 n} x_n=b_1 \\
a_{21} x_1+a_{22} x_2+\cdots+a_{2 n} x_n=b_2 \\
\vdots \\
a_{m 1} x_1+a_{m 2} x_2+\cdots+a_{m n} x_n=b_m
\end{cases}
$$
其中 $a_{i j}$ 表示 $i$ 行 $j$ 列的系数, $x_n$ 表示变量/未知数, $b_m$ 表示常数.
 增广矩阵
增广矩阵
上述方程组也可以通过矩阵系统进行简化:
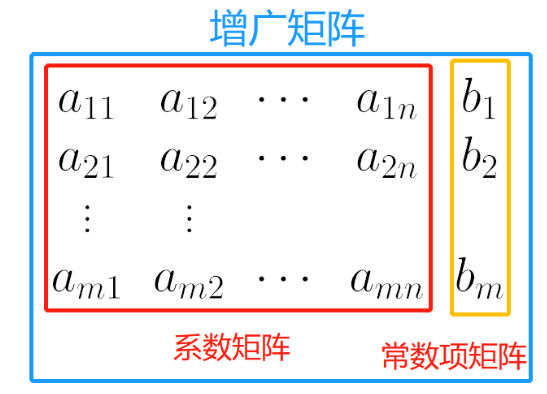
- 把系数从线性方程组中提取出来,写成的矩阵称为系数矩阵。
- 把常数项从线性方程组中提取出来,写成的矩阵称为常数项矩阵。
- 把系数矩阵和常数项矩阵左右拼接在一起,写出的矩阵称为增广矩阵。
特别地, 若 $b_1=b_2=\cdots=b_n=0$, 方程组变为:
$$
\begin{gathered}
a_{11} x_1+a_{12} x_2+\cdots+a_{1 n} x_n=0 \\
a_{21} x_1+a_{22} x_2+\cdots+a_{2 n} x_n=0 \\
\vdots \\
a_{m 1} x_1+a_{m 2} x_2+\cdots+a_{m n} x_n=0
\end{gathered}
$$
称上面线性方程组为齐次线性方程组。齐次线性方程组与其系数矩阵一一对应。
我们利用增广矩阵的方法,通过初等行变换来求解方程组:
$$
\begin{cases}
2 x-y=1 \\
x+2 y=0
\end{cases}
$$
-
首先将方程组写成增广矩阵的形式:
$$
\left[\begin{array}{cc|c}
2 & -1 & 1 \\
1 & 2 & 0
\end{array}\right]
$$ -
我们将第 1 行乘以 $\frac{1}{2}$ (记作 $R_1 \leftarrow \frac{1}{2} R_1$ ):
$$
\left[\begin{array}{cc|c}
1 & -\frac{1}{2} & \frac{1}{2} \\
1 & 2 & 0
\end{array}\right]
$$ -
我们用第 1 行消去第 2 行中的 $x$ (记作 $R_2 \leftarrow R_2-R_1$ ):
$$
\left[\begin{array}{cc|c}
1 & -\frac{1}{2} & \frac{1}{2} \\
0 & \frac{5}{2} & -\frac{1}{2}
\end{array}\right]
$$ -
我们将第 2 行乘以 $\frac{2}{5}$ (记作 $R_2 \leftarrow \frac{2}{5} R_2$ ):
$$
\left[\begin{array}{cc:c}
1 & -\frac{1}{2} & \frac{1}{2} \\
0 & 1 & -\frac{1}{5}
\end{array}\right]
$$ -
我们用第 2 行消去第 1 行中的 $y$ (记作 $R_1 \leftarrow R_1+\frac{1}{2} R_2$ ):
$$
\left[\begin{array}{cc|c}
1 & 0 & \frac{2}{5} \\
0 & 1 & -\frac{1}{5}
\end{array}\right]
$$
最终的增广矩阵表示解为:
$$
\left[\begin{array}{cc|c}
1 & 0 & \frac{2}{5} \\
0 & 1 & -\frac{1}{5}
\end{array}\right]
$$
因此,解为:
$$
x=\frac{2}{5}=0.4, \quad y=-\frac{1}{5}=-0.2
$$
这里仅以增广矩阵为例,简单说明方程组系统和矩阵系统是可以关联的。关于矩阵表示,下文还会有更加详细的讲解说明。
 向量表示
向量表示
首先看一下向量的通俗理解: 向量是一个指令,不是一个坐标,可以存在于坐标系下的任何位置。
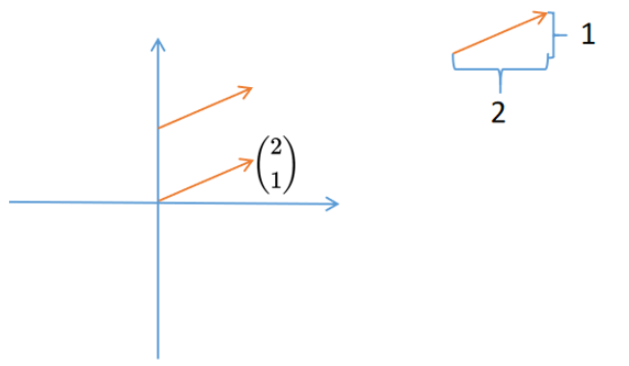
向量 $\binom{2}{1}$ 可以看作向右走两个单位, 向上走一个单位。它可以存在于坐标系下的任何位置。 $\binom{2}{1}$ 并不代表其在坐标系中的 $x$ 轴和 $y$ 轴坐标。
向量的数乘:
向量的数乘(scalor)指用一个标量来乘向量, 改变的是向量长短, 不改变方向。如:
$$
2\left[\begin{array}{l}
2 \\
1
\end{array}\right]=\left[\begin{array}{l}
4 \\
2
\end{array}\right]
$$
向量的加法:
向量的加法(vector addition)计算采用平行四边形法则(首尾相连):以同一起点的两个向量为邻边作平行四边形, 则以公共起点为起点的对角线所对应向量就是和向量。如下图:
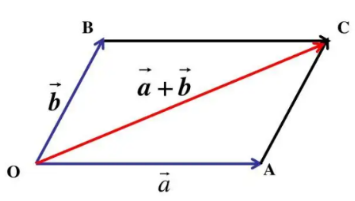
举个例子:
$$
\left[\begin{array}{l}
2 \\
1
\end{array}\right]+\left[\begin{array}{c}
-1 \\
1
\end{array}\right]=\left[\begin{array}{l}
1 \\
2
\end{array}\right]
$$
按照指令翻译的话: 向右移动两个单位 $\rightarrow$ 向上移动一个单位 $\rightarrow$ 向左移动一个单位 $\rightarrow$ 向上移动一个单位。
向量的线性组合:
向量的线性组合(linear combination)实际上就是向量数乘和向量加法的组合。可以用公式 $x_1 a_1+x_2 a_2+\cdots+x_n a_n$ 表示。其中 $x_n$ 是常数, 如:
$$
2\left[\begin{array}{l}
2 \\
1
\end{array}\right]-\left[\begin{array}{c}
-1 \\
1
\end{array}\right]=\left[\begin{array}{l}
5 \\
1
\end{array}\right]
$$
向量的线性组合与线性方程组紧密相关:当寻求向量的线性组合的解时, 实际上是在解决一个对应的线性方程组, 如:

向量空间:
向量空间指的是线性组合的集合,例如 :
$$
\boldsymbol{b}=x_1\left[\begin{array}{l}
2 \\
1
\end{array}\right]+x_2\left[\begin{array}{c}
-1 \\
1
\end{array}\right]
$$
$\boldsymbol{b}$ 的向量空间是整个二维空间。即: 在二维空间中的任何一个向量 $\boldsymbol{b}$, 都可以通过向量 $\left[\begin{array}{l}2 \\ 1\end{array}\right]$ 和 $\left[\begin{array}{c}-1 \\ 1\end{array}\right]$ 的线性组合进行表示。向量空间的严谨定义是:对向量加法和数乘 (即线性组合) 都封闭的非空集合,就是向量空间。
怎么确定一个向量 $\boldsymbol{b}$ 是否在 {$ {\boldsymbol{a}_1,\boldsymbol{a}_2,\cdots \boldsymbol{a}_n}$ }的向量空间中呢?
其实就是去求解向量 $\boldsymbol{b}$ 是否可以在向量空间中被表示。
如判断向量 $\left[\begin{array}{c}-1 \\ 4 \\ 11\end{array}\right]$ 是否存在于向量空间 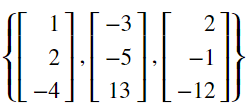
可以把这个问题转化成线性方程组求解的问题。即求解一个向量是否在向量空间中, 就是求向量对应的线性方程组是否有解。其转化成线性方程组的过程如下所示:
$$
\begin{gathered}
x_1\left[\begin{array}{r}
1 \\
2 \\
-4
\end{array}\right]+x_2\left[\begin{array}{c}
-3 \\
-5 \\
13
\end{array}\right]+x_3\left[\begin{array}{r}
2 \\
-1 \\
-12
\end{array}\right]=\left[\begin{array}{c}
-1 \\
4 \\
11
\end{array}\right] \\
{\left[\begin{array}{c}
x_1 \\
2 x_1 \\
-4 x_1
\end{array}\right]+\left[\begin{array}{c}
-3 x_2 \\
-5 x_2 \\
13 x_2
\end{array}\right]+\left[\begin{array}{c}
2 x_3 \\
-x_3 \\
-12 x_3
\end{array}\right]=\left[\begin{array}{c}
-1 \\
4 \\
11
\end{array}\right]} \\
{\left[\begin{array}{c}
x_1-3 x_2+2 x_3 \\
2 x_1-5 x_2-x_3 \\
-4 x_1+13 x_2-12 x_3
\end{array}\right]=\left[\begin{array}{c}
-1 \\
4 \\
11
\end{array}\right]} \\
{\left[\begin{array}{ccc}
1 & -3 & 2 \\
2 & -5 & -1 \\
-4 & 13 & -12
\end{array}\right]\left[\begin{array}{l}
x_1 \\
x_2 \\
x_3
\end{array}\right]=\left[\begin{array}{c}
-1 \\
4 \\
11
\end{array}\right]}
\end{gathered}
$$
求解的话可以转换成增广矩阵再进行求解。最后可解得:
$$
\begin{aligned}
& x_1=30 \\
& x_2=11 \\
& x_3=1
\end{aligned} \Rightarrow \boldsymbol{x}=\left[\begin{array}{c}
30 \\
11 \\
1
\end{array}\right]
$$
线性相关和线性无关
如果 $x_1 \boldsymbol{a}_1+x_2 \boldsymbol{a}_2+\cdots+x_n \boldsymbol{a}_n=\mathbf{0}$, 可以找到至少一个 $x_i$ 不为 0 , 即 $x_1, x_2, \cdots, x_n$ 不全为 0 ,则 {$ {\boldsymbol{a}_1,\boldsymbol{a}_2,\cdots \boldsymbol{a}_n}$ } 线性相关。
如果 $x_1 \boldsymbol{a}_1+x_2 \boldsymbol{a}_2+\cdots+x_n \boldsymbol{a}_n=\mathbf{0}$, 只在 $x_1=x_2=\cdots=x_n=0$ 的情况下成立, 则 {$ {\boldsymbol{a}_1,\boldsymbol{a}_2,\cdots \boldsymbol{a}_n}$ }线性无关。
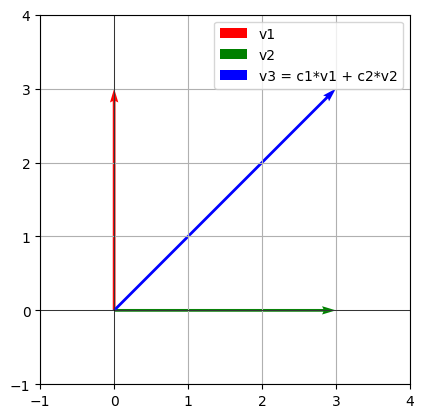
关于线性相关性存在一个定理: $n+1$ 个 $n$ 维向量必线性相关。例如三个 3 维向量可以线性无关, 但三个 2 维向量一定线性相关。
import matplotlib.pyplot as plt
import numpy as np
# 定义向量
v1 = np.array([0, 3])
v2 = np.array([3, 0])
v3 = np.array([3, 3]) # 这里 v3 是 v1 和 v2 的线性组合
# 绘制向量
fig, ax = plt.subplots()
ax.quiver(0, 0, v1[0], v1[1], angles='xy', scale_units='xy', scale=1, color='r', label='v1')
ax.quiver(0, 0, v2[0], v2[1], angles='xy', scale_units='xy', scale=1, color='g', label='v2')
ax.quiver(0, 0, v3[0], v3[1], angles='xy', scale_units='xy', scale=1, color='b', label='v3 = c1*v1 + c2*v2')
# 设置图形属性
ax.set_xlim(-1, 4)
ax.set_ylim(-1, 4)
ax.set_aspect('equal')
plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.legend()
# 显示图形
plt.show()
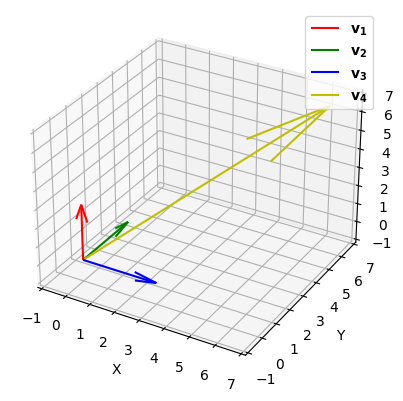
from mpl_toolkits.mplot3d import Axes3D
# Define vectors
v1 = np.array([0, 0, 3])
v2 = np.array([0, 3, 0])
v3 = np.array([3, 0, 0])
v4 = np.array([6, 7, 6]) # v4 is a linear combination of v1, v2, and v3
# Create 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Plotting vectors
ax.quiver(0, 0, 0, v1[0], v1[1], v1[2], color='r', label='$\mathbf{v_1}$')
ax.quiver(0, 0, 0, v2[0], v2[1], v2[2], color='g', label='$\mathbf{v_2}$')
ax.quiver(0, 0, 0, v3[0], v3[1], v3[2], color='b', label='$\mathbf{v_3}$')
ax.quiver(0, 0, 0, v4[0], v4[1], v4[2], color='y', label='$\mathbf{v_4}$')
# Setting plot attributes
ax.set_xlim([-1, 7])
ax.set_ylim([-1, 7])
ax.set_zlim([-1, 7])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.legend()
# Show plot
plt.show()
向量的点积和内积(Inner Product, dot product):
向量的点积和内积 (Inner Product, dot product), 用・表示, 两个向量的行列数必须相同, 点积的结果是对应元素相乘后求和, 结果是一个标量, 如:
$$
\begin{aligned}
& \boldsymbol{a}=\left(a_1, a_2, \cdots, a_n\right) \\
& \boldsymbol{b}=\left(b_1, b_2, \cdots, b_n\right) \\
& \boldsymbol{a} \cdot \boldsymbol{b}=a_1 b_1+a_2 b_2+\cdots+a_n b_n
\end{aligned}
$$
点积的几何意义可以用来计算两个向量的夹角: $\cos \theta=\frac{\boldsymbol{a} \boldsymbol{b}}{|\boldsymbol{a}||\boldsymbol{b}|}$
至于向量长度的求解, $n$ 维向量的长度: $|\boldsymbol{x}|=\sqrt{[x, x]}=\sqrt{x_1^2+x_2^2+\cdots+x_n^2} \geq 0$, 当 $|x|=1$ 时称为单位向量。
tips: Dot product 和 Inner product其实还是有区别的,点积主要应用于欧几里得空间(即普通的二维或三维空间);而内积是点积的一个广义概念,它不仅仅局限于欧几里得空间,还可以应用于更广泛的向量空间,例如复数空间或更抽象的希尔伯特空间。目前阶段暂时将二者视为同一个概念即可。
向量的外积:
向量的外积 (Outer product), 用 $\otimes$ 表示, 如:
$$
\begin{aligned}
& \boldsymbol{u}=\left(u_1, u_2, \cdots, u_m\right) \\
& \boldsymbol{v}=\left(v_1, v_2, \cdots, v_n\right) \\
& \boldsymbol{u} \otimes \boldsymbol{v}=\left[\begin{array}{cccc}
u_1 v_1 & u_1 v_2 & \cdots & u_1 v_n \\
u_2 v_1 & u_2 v_2 & \cdots & u_2 v_n \\
\vdots & \vdots & \ddots & \vdots \\
u_m v_1 & u_m v_2 & \cdots & u_m v_n
\end{array}\right]
\end{aligned}
$$
向量的叉积:
向量的叉积 (Outer product), 用 $\times$ 表示, 如:
$$
\begin{aligned}
& \boldsymbol{a}=\left(x_1, y_1, z_1\right) \\
& \boldsymbol{b}=\left(x_2, y_2, z_2\right) \\
& \boldsymbol{a} \times \boldsymbol{b}=\left|\begin{array}{lll}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
x_1 & y_1 & z_1 \\
x_2 & y_2 & z_2
\end{array}\right|=\left(y_1 z_2-y_2 z_1\right) \boldsymbol{i}+\left(z_1 x_2-z_2 x_1\right) \boldsymbol{j}+\left(x_1 y_2-x_2 y_1\right) \boldsymbol{k} \\
& \boldsymbol{i}=[1,0,0], \boldsymbol{j}=[0,1,0], \boldsymbol{k}=[0,0,1]
\end{aligned}
$$
叉积计算结果的几何意义是两个向量的法向量。
举个例子: $\boldsymbol{a}$是 $x$ 轴的单位向量, $\boldsymbol{b}$ 是 $y$ 轴的单位向量, 二者叉积的结果就是 $z$ 轴的单位向量, 即:
$$
\begin{aligned}
& \boldsymbol{a}=(1,0,0) \\
& \boldsymbol{b}=(0,1,0) \\
& \boldsymbol{i}=(1,0,0) \\
& \boldsymbol{j}=(0,1,0) \\
& \boldsymbol{k}=(0,0,1) \\
& \boldsymbol{a} \times \boldsymbol{b}=\left|\begin{array}{lll}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array}\right|=(0 \times 0-0 \times 1) \boldsymbol{i}+(0 \times 0-0 \times 1) \boldsymbol{j}+(1 \times 1-0 \times 0) \boldsymbol{k}=\boldsymbol{k}
\end{aligned}
$$
正交与基组
正交是指两个向量的内积为零的情况。在欧几里得空间中,如果两个向量的点积为零,它们被称为正交向量。
对于两个向量 $\mathbf{u}$ 和 $\mathbf{v}$ ,如果:
$$
\mathbf{u} \cdot \mathbf{v}=0
$$
那么这两个向量就是正交的。正交向量具有一些重要性质:
- 独立性: 正交向量一定是线性无关的。
- 长度不变性: 正交向量的长度在内积运算中保持不变。
- 投影: 任意向量在正交向量上的投影计算非常简单。
基组是指向量空间中一组线性无关的向量,这组向量的线性组合可以表示该空间中的任意向量。基组的个数等于向量空间的维数。
设 $V$ 是一个 $n$ 维向量空间,如果向量集合 {$ {\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots \boldsymbol{v}_n}$ }满足以下条件:
- 线性无关:集合中的向量彼此线性无关。
- 生成整个空间: 集合中的向量的线性组合可以生成 $V$ 中的任意向量。
那么,集合 {$ {\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots \boldsymbol{v}_n}$ } 就是 $V$ 的一个基组。基组的概念在数学中是非常基础和重要的,它提供了一种对向量空间进行描述和操作的方法。
在许多应用中,我们更希望使用正交基或标准正交基:
- 正交基:如果基组中的向量两两正交,则称为正交基。
- 标准正交基:如果基组中的向量两两正交且每个向量的长度为1,则称为标准正交基。
标准正交基具有以下优点:
- 简化计算: 向量的表示和运算(如内积、投影)变得更加简单。
- 稳定性:在数值计算中,标准正交基可以减少误差累积。
 矩阵表示
矩阵表示
矩阵乘法
矩阵乘法 (Matmul Product) 是两个矩形相乘的操作, 其结果是另一个矩阵。定义如下:设有两个矩阵 $\boldsymbol{A}$ 和 $\boldsymbol{B}$, 令 $\boldsymbol{A}$ 是一个 $m \times n$ 的矩阵, 而 $\boldsymbol{B}$ 是一个 $n \times p$ 的矩阵。那么矩阵 $\boldsymbol{A}$和 $\boldsymbol{B}$ 的乘积 $\boldsymbol{C}$ 是一个 $m \times p$ 的矩阵, 每个元素由以下公式给出:
$$
\boldsymbol{C}_{i j}=\sum_{k=1}^n \boldsymbol{A}_{i k} \boldsymbol{B}_{k j}
$$
其中 $\boldsymbol{C}_{i j}$ 是结果矩阵 $\boldsymbol{C}$ 的第 $i$ 行第 $j$ 列的元素。
设有矩阵 $\boldsymbol{A}$ 和 $\boldsymbol{B}$ 如下:
$$
\begin{aligned}
\boldsymbol{A} & =\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right] \\
\boldsymbol{B} & =\left[\begin{array}{ll}
2 & 0 \\
1 & 3
\end{array}\right]
\end{aligned}
$$
计算 $\boldsymbol{A} \times \boldsymbol{B}$ 的结果为:
$$
\boldsymbol{A} \times \boldsymbol{B}=\left[\begin{array}{cc}
4 & 6 \\
10 & 12
\end{array}\right]
$$
哈达玛积
哈达玛积(Element-wise Product)表示两个矩阵对应元素相乘, 二者维数必须相同, 用 $\odot$ 表示。如:
$$
\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right] \odot\left[\begin{array}{ll}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{array}\right]=\left[\begin{array}{ll}
a_{11} b_{11} & a_{12} b_{12} \\
a_{21} b_{21} & a_{22} b_{22}
\end{array}\right]
$$
克罗内克积
克罗内克积 (Kronecker Product) 表示两个任意大小矩阵间的运算, 矩阵 $\boldsymbol{A}$ 的每个元素逐个与矩阵 $\boldsymbol{B}$ 相乘, 用 $\otimes$ 表示。如:
$$
\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right] \otimes\left[\begin{array}{ll}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{array}\right]=\left[\begin{array}{llll}
a_{11} b_{11} & a_{11} b_{12} & a_{12} b_{11} & a_{12} b_{12} \\
a_{11} b_{21} & a_{11} b_{22} & a_{12} b_{21} & a_{12} b_{22} \\
a_{21} b_{11} & a_{21} b_{12} & a_{22} b_{11} & a_{22} b_{12} \\
a_{21} b_{21} & a_{21} b_{22} & a_{22} b_{21} & a_{22} b_{22}
\end{array}\right]
$$
初等矩阵
矩阵可以看作对向量的变换,单位矩阵是对角线全1的矩阵,相当于0变换。
$$
\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]=\boldsymbol{I}
$$
可以发现初等矩阵是对角矩阵, 如果一个对角矩阵的值不为 1 会对向量产生什么影响呢?
import numpy as np
import matplotlib.pyplot as plt
# 定义原始向量
vector = np.array([1, 1])
# 定义对角矩阵
diagonal_matrix = np.array([[3, 0],
[0, 2]])
# 对向量应用对角矩阵变换
transformed_vector = diagonal_matrix @ vector
# 设置绘图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
# 第一个子图:填充变换前的阴影
ax1.axhline(0, color='grey', lw=0.5)
ax1.axvline(0, color='grey', lw=0.5)
ax1.grid(True, which='both')
# 绘制原始向量
ax1.quiver(0, 0, vector[0], vector[1], angles='xy', scale_units='xy', scale=1, color='blue', label='Original Vector')
# 绘制变换后的向量
ax1.quiver(0, 0, transformed_vector[0], transformed_vector[1], angles='xy', scale_units='xy', scale=1, color='red', label='Transformed Vector')
# 填充原始向量所在的矩形区域
ax1.fill([0, vector[0], vector[0], 0], [0, 0, vector[1], vector[1]], color='blue', alpha=0.1)
# 设置坐标轴范围
ax1.set_xlim(-2, 5)
ax1.set_ylim(-2, 5)
# 设置坐标轴刻度为1
ax1.set_xticks(np.arange(-2, 6, 1))
ax1.set_yticks(np.arange(-2, 6, 1))
# 添加图例
ax1.legend()
ax1.set_title('Original Vector Shadow')
# 第二个子图:填充变换后的阴影
ax2.axhline(0, color='grey', lw=0.5)
ax2.axvline(0, color='grey', lw=0.5)
ax2.grid(True, which='both')
# 绘制原始向量
ax2.quiver(0, 0, vector[0], vector[1], angles='xy', scale_units='xy', scale=1, color='blue', label='Original Vector')
# 绘制变换后的向量
ax2.quiver(0, 0, transformed_vector[0], transformed_vector[1], angles='xy', scale_units='xy', scale=1, color='red', label='Transformed Vector')
# 填充变换后向量所在的矩形区域
ax2.fill([0, transformed_vector[0], transformed_vector[0], 0], [0, 0, transformed_vector[1], transformed_vector[1]], color='red', alpha=0.1)
# 设置坐标轴范围
ax2.set_xlim(-2, 5)
ax2.set_ylim(-2, 5)
# 设置坐标轴刻度为1
ax2.set_xticks(np.arange(-2, 6, 1))
ax2.set_yticks(np.arange(-2, 6, 1))
# 添加图例
ax2.legend()
ax2.set_title('Transformed Vector Shadow')
# 显示图形
plt.tight_layout()
plt.show()
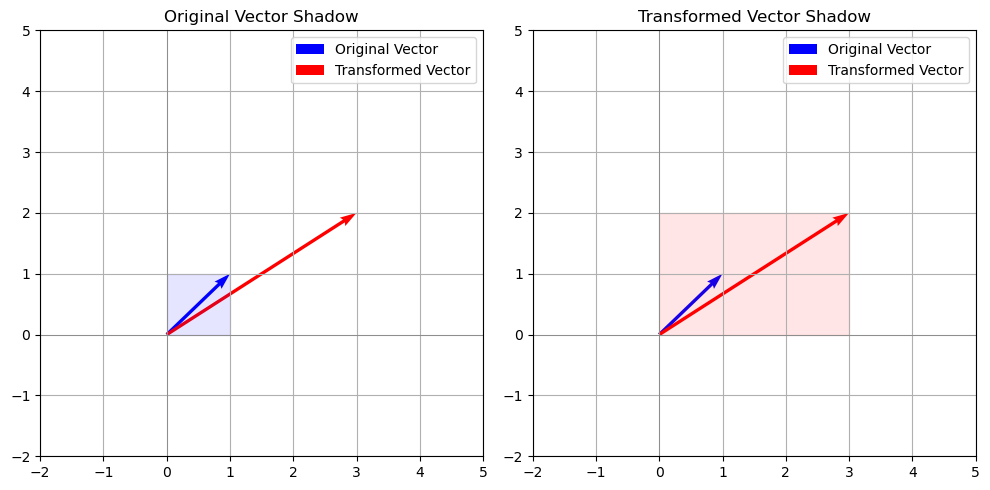
可以发现,此时的影响是在x轴或y轴上对向量进行伸缩。那么普通的矩阵又是什么效果呢?
普通的矩阵还可以对向量产生旋转的变换效果
可逆矩阵
在线性代数中,可逆矩阵 (Invertible Matrix),又称为非奇异矩阵 (Non-Singular Matrix) 或满秩矩阵 (Full-Rank Matrix),是指存在唯一逆矩阵的方阵。一个 $n \times n$ 的方阵 $A$ 称为可逆的,如果存在另一个 $n \times n$ 的矩阵 $B$ ,使得:
$$
A \cdot B=B \cdot A=I
$$
其中, $I$ 是 $n \times n$ 的单位矩阵(对角线上的元素全为 1 ,其余元素全为 0 ),而矩阵 $B$ 就是矩阵 $A$的逆矩阵,记作 $A^{-1}$ 。
可逆矩阵在许多数学和工程领域有广泛的应用,包括:
- 解线性方程组。
- 线性变换中的变换矩阵。
- 计算矩阵函数(如矩阵指数)。
- 数据分析中的主成分分析(PCA)。
举例:可逆矩阵把求解向量$x$的问题转换成了求可逆矩阵本身的问题,如下公式推导所示:
$$
\begin{aligned}
& A x=b \\
& A^{-1} A x=A^{-1} b \\
& x=A^{-1} b
\end{aligned}
$$
可逆矩阵的求解与矩阵 $\boldsymbol{A}$ 和初等矩阵 $\boldsymbol{I}$ 有关, 具体推导如下:
假设 $\boldsymbol{A}=\left[\begin{array}{ccc}1 & -2 & 1 \\ -3 & 7 & -6 \\ 2 & -3 & 0\end{array}\right]$, 求可逆矩阵 $\boldsymbol{A}^{-1}$ 的过程如下:
$$
\left[\begin{array}{ccc:ccc}
1 & -2 & 1 & 1 & 0 & 0 \\
-3 & 7 & -6 & 0 & 1 & 0 \\
2 & -3 & 0 & 0 & 0 & 1
\end{array}\right] \Rightarrow\left[\begin{array}{lll:lll}
1 & 0 & 0 & -18 & -3 & 5 \\
0 & 1 & 0 & -12 & -2 & 3 \\
0 & 0 & 1 & -5 & -1 & 1
\end{array}\right]
$$
通过矩阵的初等行变换将左边矩阵推导成右面的格式即完成了可逆矩阵的计算, 此时可逆矩阵: $\boldsymbol{A}^{-1}=\left[\begin{array}{ccc}-18 & -3 & 5 \\ -12 & -2 & 3 \\ -5 & -1 & 1\end{array}\right]$ 。
行列式
这里就先谈行列式的几何意义,最后再谈行列式的计算方法的由来。
思考一下,经过线性变换(矩阵相乘),空间发生了变化,相应的面积也会发生变化。我们可以将行列式理解为线性变换对空间(包括面积、体积等)的缩放比例因子。
考虑二维空间中的一个矩形,其顶点分别为 $(0,0) 、(1,0) 、(0,1) 、(1,1)$ 。如果我们对这个矩形进行线性变换,即通过矩阵 $A$ 作用在它上面,这个矩形会变形为一个平行四边形。
假设矩阵 $A$ 为:
$$
A=\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)
$$
经过矩阵 $A$ 的线性变换后,基向量 $(1,0)$ 和 $(0,1)$ 分别变为 $(a, c)$ 和 $(b, d)$ 。变换后的平行四边形的顶点变为 $(0,0) 、(a, c) 、(b, d) 、(a+b, c+d)$ 。
此时,平行四边形的面积可以通过行列式计算:
$$
\text { 面积 }=|\operatorname{det}(A)|=|a d-b c|
$$
行列式的绝对值表示线性变换后面积的比例因子。正值表示变换保持了原来的方向,负值表示变换翻转了方向。
import matplotlib.pyplot as plt
import numpy as np
# 定义原始单位正方形的顶点
square = np.array([[0, 0], [1, 0], [1, 1], [0, 1], [0, 0]])
# 定义矩阵 A
A = np.array([[2, 1], [1, 3]])
# 线性变换后的顶点
transformed_square = square @ A.T
# 绘制原始单位正方形
plt.plot(square[:, 0], square[:, 1], 'b-', label='orginal')
# 绘制线性变换后的平行四边形
plt.plot(transformed_square[:, 0], transformed_square[:, 1], 'r-', label='transformer')
# 设置图形属性
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(True)
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
# 显示图形
plt.show()
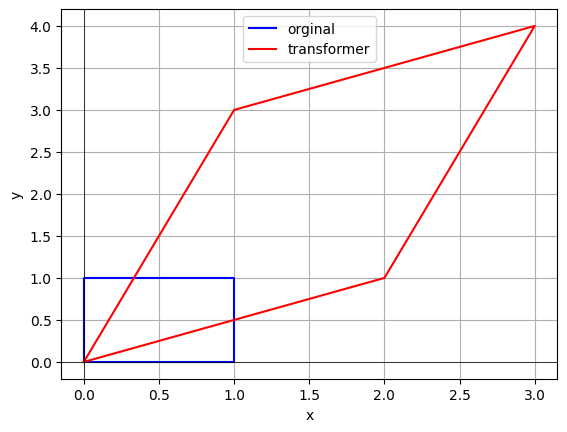
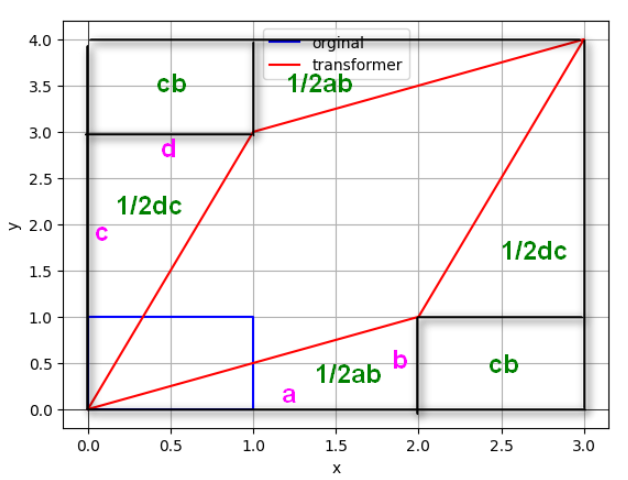
由于求的是平行四边形的面积, 从图上构建出整个长方形, 得到每一部分区域, 做减法就可以得到结果了, 整个减法如下:
$(a+c)*(b+d)-2*(1/2ab)-2*(1/2cd)-2cb=ad-bc$
对于矩阵 $A$ :
$$
A=\left(\begin{array}{ll}
2 & 1 \\
1 & 3
\end{array}\right)
$$
计算行列式:
$$
\operatorname{det}(A)=2 \cdot 3-1 \cdot 1=6-1=5
$$
因此,矩阵 $A$ 构成的平行四边形的面积是行列式的绝对值,即:
$$
|\operatorname{det}(A)|=5
$$
这与行列式的定义相符,我们可以使用 Python 来验证这一计算:
import numpy as np
# 定义矩阵 A
A = np.array([[2, 1], [1, 3]])
# 计算行列式
det_A = np.linalg.det(A)
int(det_A)
5在上面的基础上来考虑行列式为0,或1时候,代表什么?
行列式为零:
行列式的几何意义是线性变换对面积或体积的缩放比例因子。当行列式为零时,意味着变换后的面积或体积为零,即原来的几何结构被完全压缩,没有扩展到原来的维度。
假设矩阵 $A$ 为:
$$
A=\left(\begin{array}{ll}
1 & 2 \\
2 & 4
\end{array}\right)
$$
计算行列式:
$$
\operatorname{det}(A)=1 \cdot 4-2 \cdot 2=4-4=0
$$
import matplotlib.pyplot as plt
import numpy as np
# 定义原始单位正方形的顶点
square = np.array([[0, 0], [1, 0], [1, 1], [0, 1], [0, 0]])
# 定义行列式为零的矩阵 A
A = np.array([[1, 2], [2, 4]])
# 线性变换后的顶点
transformed_square = square @ A.T
# 绘制原始单位正方形
plt.plot(square[:, 0], square[:, 1], 'b-', label='orginal')
# 绘制线性变换后的图形
plt.plot(transformed_square[:, 0], transformed_square[:, 1], 'r-', label='transformed')
# 绘制坐标轴
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
# 绘制点
plt.scatter([0, A[0, 0], A[0, 1]], [0, A[1, 0], A[1, 1]], color='r')
# 标注点
plt.text(0, 0, 'O', fontsize=12, ha='right')
plt.text(A[0, 0], A[1, 0], 'A', fontsize=12, ha='right')
plt.text(A[0, 1], A[1, 1], 'B', fontsize=12, ha='right')
# 设置图形属性
plt.grid(True)
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
# 显示图形
plt.show()
当一个矩阵的行列式为1时,几何上意味着该矩阵对应的线性变换保持面积(或体积)不变,同时也保持方向不变。简单来说,这种变换只对空间进行旋转或拉伸,而不会改变面积或体积。
import matplotlib.pyplot as plt
import numpy as np
# 定义原始单位正方形的顶点
square = np.array([[0, 0], [1, 0], [1, 1], [0, 1], [0, 0]])
# 定义行列式为1的矩阵 A
A = np.array([[1, 2], [0, 1]])
# 线性变换后的顶点
transformed_square = square @ A.T
# 绘制原始单位正方形
plt.plot(square[:, 0], square[:, 1], 'b-', label='orginal')
# 绘制线性变换后的图形
plt.plot(transformed_square[:, 0], transformed_square[:, 1], 'r-', label='transformed')
# 绘制坐标轴
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
# 绘制点
plt.scatter([0, A[0, 0], A[0, 1]], [0, A[1, 0], A[1, 1]], color='r')
# 标注点
plt.text(0, 0, 'O', fontsize=12, ha='right')
plt.text(A[0, 0], A[1, 0], 'A', fontsize=12, ha='right')
plt.text(A[0, 1], A[1, 1], 'B', fontsize=12, ha='right')
# 设置图形属性
plt.grid(True)
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
# 显示图形
plt.show()
矩阵的秩
秩表示什么呢? 假设四个行向量组成的矩阵 $\boldsymbol{A}$ 如下:
$$
\begin{aligned}
\boldsymbol{\alpha}_1 & =(1,1,3,1), \boldsymbol{\alpha}_2=(0,2,-1,4), \\
\boldsymbol{\alpha}_3 & =(0,0,0,5), \boldsymbol{\alpha}_4=(0,0,0,0) . \\
\boldsymbol{A} & =\left[\begin{array}{cccc}
1 & 1 & 3 & 1 \\
0 & 2 & -1 & 4 \\
0 & 0 & 0 & 5 \\
0 & 0 & 0 & 0
\end{array}\right]
\end{aligned}
$$
求其极大线性无关组:
假设有: $k_1 \boldsymbol{\alpha}_1+k_2 \boldsymbol{\alpha}_2+k_3 \boldsymbol{\alpha}_3=0$ (因为 $\boldsymbol{\alpha}_4$ 是零向量, 跟谁都有关, 所以只假设前三个向量线性相关)。
$$
\begin{cases}
k_1=0, \\
k_1+2 k_2=0, \\
3 k_1-k_2=0, \\
k_1+4 k_2+5 k_3=0
\end{cases}
$$
解得: $k_1=k_2=k_3=0$, 即 $\alpha_1, \alpha_2, \alpha_3$ 线性无关。
矩阵的秩表示当前矩阵中线性无关的向量组的个数, 在当前例子中即为 3 。
在之前说过矩阵可以看作对向量做变换, 例如可以对二维图形进行旋转, 比如用旋转矩阵 $\left[\begin{array}{cc}\cos (\theta) & -\sin (\theta) \\ \sin (\theta) & \cos (\theta)\end{array}\right]$ 。
此时的旋转矩阵秩为 2, 变换后的效果如下。
import matplotlib.pyplot as plt
import numpy as np
# 定义旋转矩阵
theta = np.pi / 4 # 45 degrees
rotation_matrix = np.array([
[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]
])
A = np.array([[1, -1], [1, -1]])
# 定义一个二维图形(例如一个正方形)
square = np.array([[1, 1], [-1, 1], [-1, -1], [1, -1], [1, 1]])
# 旋转后的图形
rotated_square = square @ rotation_matrix.T
# 绘制原始图形
plt.plot(square[:, 0], square[:, 1], 'b-', label='orginal')
# 绘制旋转后的图形
plt.plot(rotated_square[:, 0], rotated_square[:, 1], 'r-', label='transformed')
# 设置图形属性
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid(True)
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
# 显示图形
plt.show()
变换后的结果依然是二维的。如果用矩阵 $\left[\begin{array}{ll}1 & -1 \\ 1 & -1\end{array}\right]$ 进行变换呢? 此时矩阵的秩为 1 , 变换效果如何?
变换后的结果变成了一维。这里就体现出矩阵的秩对向量的变换作用。即:如果矩阵的秩低于向量空间的维度,那么会对向量进行降维。
最后强调一下,矩阵的秩实际上代表了矩阵中不重复的主要特征个数。
举个生活中的例子:家里的有三只小猫咪,给它们拍摄了100张照片,组成了十行十列的矩阵,该矩阵的秩等于3,就算拍一千张照片,组成的矩阵秩还是3。
矩阵的特征值与特征向量
通俗的理解特征值和特征向量描述了什么,怎么获得成功的人生?在正确的道路上坚持努力下去。可以把千百种人生选择看作特征向量(它是有方向的!);把在这个方向上的努力看作特征值(它是一个衡量大小的量)。
下面引出它的数学定义: 对于给定矩阵 $\boldsymbol{A}$, 寻找一个常数 $\lambda$ 和非零向量 $\boldsymbol{x}$, 使得向量 $\boldsymbol{x}$被矩阵 $\boldsymbol{A}$ 作用后, 所得的向量 $\boldsymbol{A x}$ 与原向量 $\boldsymbol{x}$ 平行,
并且满足 $\boldsymbol{A x}=\lambda \boldsymbol{x}$ 。其中, $\boldsymbol{x}$ 是特征向量, $\lambda$ 是特征值, 特征值越大表示该特征向量越重要。
举个例子来理解:
向量 $\boldsymbol{e}_1=\left[\begin{array}{l}1 \\ 0\end{array}\right]$ 和向量 $\boldsymbol{e}_2=\left[\begin{array}{l}0 \\ 1\end{array}\right]$ 都是向量 $\boldsymbol{A}=\left[\begin{array}{ll}3 & 0 \\ 0 & 2\end{array}\right]$ 的特征向量。
因为它们都可写成 $\boldsymbol{A} \boldsymbol{x}=\lambda \boldsymbol{x}$ 的形式:
$$
\begin{aligned}
A e_1 & =\left[\begin{array}{ll}
3 & 0 \\
0 & 2
\end{array}\right]\left[\begin{array}{l}
1 \\
0
\end{array}\right]=\left[\begin{array}{l}
3 \\
0
\end{array}\right]=3 e_1 \\
A e_2 & =\left[\begin{array}{ll}
3 & 0 \\
0 & 2
\end{array}\right]\left[\begin{array}{l}
0 \\
1
\end{array}\right]=\left[\begin{array}{l}
0 \\
2
\end{array}\right]=2 e_2
\end{aligned}
$$
特征向量有无数个,且此时特征向量在应用原始向量A后,只有伸缩作用,没有旋转作用,伸缩的比例就是特征值。具体来说:
- 对于 $\mathbf{e}_1$ ,矩阵 $A$ 将其拉伸 3 倍(特征值为 3 )。
- 对于 $\mathbf{e}_2$ ,矩阵 $A$ 将其拉伸 2 倍(特征值为 2 )。
最后,怎么求解特征向量呢?公式如下:
$$
\begin{aligned}
& A \boldsymbol{x}=\lambda \boldsymbol{x} \\
& \boldsymbol{A} \boldsymbol{x}=\lambda(\boldsymbol{I} \boldsymbol{x})=\lambda \boldsymbol{I} \boldsymbol{x} \\
& (\boldsymbol{A}-\lambda \boldsymbol{I}) \boldsymbol{x}=\mathbf{0}
\end{aligned}
$$
此时,解特征向量变成了求解齐次方程的问题。
例如求 $\boldsymbol{A}=\left[\begin{array}{ll}2 & 0 \\ 0 & 3\end{array}\right]$ 的特征值。
$$
\begin{aligned}
& |\boldsymbol{A}-\lambda \boldsymbol{I}|=0 \\
& \boldsymbol{X}=\left[\begin{array}{ll}
2 & 0 \\
0 & 3
\end{array}\right]-\lambda \boldsymbol{I}=\left[\begin{array}{cc}
2-\lambda & 0 \\
0 & 3-\lambda
\end{array}\right] \\
& \operatorname{det}(\boldsymbol{X})=(2-\lambda) *(3-\lambda)
\end{aligned}
$$
很容易看出 $\lambda_1=2, \lambda_2=3$ 。把 $\lambda$ 代入式 $\boldsymbol{A} \boldsymbol{v}=\lambda \boldsymbol{v}$ :
$\left[\begin{array}{ll}2 & 0 \\ 0 & 3\end{array}\right]\left[\begin{array}{l}v_i \\ v_j\end{array}\right]=\left[\begin{array}{l}2 v_i \\ 3 v_j\end{array}\right]=2 \cdot\left[\begin{array}{l}v_i \\ v_j\end{array}\right]$ 此式在 $v_j=0$ 时对任何 $v_i$ 成立
$\left[\begin{array}{ll}2 & 0 \\ 0 & 3\end{array}\right]\left[\begin{array}{l}v_i \\ v_j\end{array}\right]=\left[\begin{array}{l}2 v_i \\ 3 v_j\end{array}\right]=3 \cdot\left[\begin{array}{l}v_i \\ v_j\end{array}\right]$ 此式在 $v_i=0$ 时对任何 $v_j$ 成立
说明, $x$ 轴和 $y$ 轴上所有的向量都是特征向量, 且经过矩阵 $\boldsymbol{A}$ 的作用, 会在 $x$ 轴上拉伸两倍, 在 $y$ 轴上拉伸 3 倍。
作者
arwin.yu.98@gmail.com