Deep Learning Math

---

量子力学（Quantum mechanics）

---

量子力学是研究微观物理世界中粒子行为的科学，尤其是在原子和亚原子尺度上。学习几何深度学习之前，了解量子力学中球谐函数和径向模型的概念是有其重要性的，特别是当研究或应用需要处理三维数据或进行复杂的空间分析时。

球谐函数提供了一种有效的方法来表示球面上的函数，这在处理三维几何结构，如建模天体，原子，分子等球形结构时非常有用。通过球谐函数，可以在球面上展开复杂的形状和模式，为深度学习模型提供一种强大的方式来捕捉和学习这些形状的特征。另一方面，在处理三维空间数据时，旋转不变性是一个关键问题。球谐函数具有天然的旋转不变性特性，这意味着它们可以帮助构建对旋转不敏感的模型，提高模型泛化能力。

径向模型对于描述空间中点与点之间的关系非常有效。在几何深度学习中，建模物体内部或不同物体之间的空间关系是很重要的。径向基函数能够捕捉这些复杂的空间模式，并在诸如分子动力学模拟、蛋白质结构预测等领域发挥作用。更重要的是，几何深度学习经常需要在不同的尺度上分析数据。径向模型可以提供一个自然的框架来实现这一点，因为它们可以在不同的尺度上调整，从而允许模型同时学习局部和全局特征。这对于理解和处理复杂的三维结构特别有价值。

Agenda

---

• 量子力学简介

• 对称性(Symmetry)

• 不变性(Invariance)

• 等变性(Equivariance)

• S0(3) Group

• 群的表示(Representation of Groups)

量子力学（Quantum mechanics）

---

量子力学是现代物理学的一大基础理论，描述了微观世界中粒子的行为。它的发展改变了我们对自然界基本规律的理解。量子力学的形成是20世纪初一系列革命性发现的结果。以下是一些关键人物和事件：

• 马克斯·普朗克（Max Planck）：1900年，普朗克提出了量子假说与普朗克常数，以解释黑体辐射问题。他提出能量是以离散的量子形式传递的，这一理论标志着量子力学的诞生。普朗克的研究揭示了能量量子化的概念，突破了经典物理学的局限。

• 阿尔伯特·爱因斯坦（Albert Einstein）：1905年，爱因斯坦提出了光量子理论，解释了光电效应。他提出光可以被看作是由光子组成的，光子的能量与其频率成正比。爱因斯坦的光量子假设不仅验证了普朗克的量子假说，还解释了为什么某些频率的光能够释放电子，而其他频率的光则不能。

• 尼尔斯·玻尔（Niels Bohr）：玻尔在1913年提出了玻尔模型，用以解释氢原子的光谱。他的模型结合了量子理论和经典物理学，假设电子在原子核周围的轨道上运动时具有离散的能级。玻尔模型成功解释了氢原子发射和吸收光的特定频率。

• 维尔纳·海森堡（Werner Heisenberg）：1925年，海森堡提出了矩阵力学，这是一种描述量子系统的数学方法。他的矩阵力学摒弃了经典轨道的概念，转而使用算符和矩阵来描述量子态的变化。海森堡的工作奠定了量子力学的数学基础，并引入了不确定性原理。

• 埃尔温·薛定谔（Erwin Schrödinger）：1926年，薛定谔提出了薛定谔方程，描述了量子态随时间的演化。他的波动方程是量子力学的核心，提供了一种描述粒子波函数的方法。薛定谔方程不仅能够解释电子在原子中的行为，还可以应用于更复杂的量子系统。这一方程是量子力学的基础，类似于经典力学中的牛顿第二定律。

量子力学的核心问题之一就是求解薛定谔方程。求解薛定谔方程可以得到系统的波函数，从而推导出系统的能量本征值和本征态、概率密度分布、各种物理量的期望值、系统的动态演化行为以及量子态的叠加和纠缠。这些结果不仅帮助我们理解微观粒子的行为，还广泛应用于物理、化学和材料科学等领域，为现代科学技术的发展提供了重要的理论基础。

传统计算方法包括密度泛函理论（DFT）、哈特里-福克方法（Hartree-Fock）以及后哈特里-福克方法（如配置相互作用CI和耦合簇CC）。这些方法具有高度的准确性，但计算复杂度极高。通常随系统规模的指数增长。例如，CI和CC方法的计算时间和内存需求随电子数目增加而呈指数级增长，使得大规模系统的模拟几乎不可能实现。

因此，传统方法通常适用于小分子或中等规模系统，对于大分子、材料和生物大分子，计算变得极为困难。即使是中等规模系统，计算也可能耗费数小时、数天甚至数周的时间，不适合快速迭代和大规模筛选。

由于传统量子力学和量子化学方法的计算限制，科学家们开始寻求新的计算方法。深度学习模型，如SchNet等，通过学习大量量子力学计算数据，能够显著提高计算效率和时间。

这些深度学习模型并非凭空构建，而是建立在量子力学的坚实基础上，特别是几何特性和对称性。这些基础包括球谐函数、Wigner-D矩阵、CG系数和径向模型等。

• 球谐函数（Spherical Harmonics）

  • 定义：球谐函数是定义在球面上的一组正交函数，通常用于描述三维空间中的角度依赖性。
  • 应用：在量子力学中，球谐函数用于解决具有球对称性系统（如原子）的薛定谔方程，特别是在描述电子的角动量和轨道。
  • 在几何深度学习中的应用：球谐函数帮助深度学习模型捕捉分子和材料系统中的几何对称性和旋转不变性。

• Wigner-D矩阵

  • 定义：Wigner-D矩阵是表示旋转群的一组矩阵，用于描述量子系统在不同旋转下的变化。
  • 应用：在量子力学中，Wigner-D矩阵用于描述带有角动量的系统在旋转下的变换性质。
  • 在几何深度学习中的应用：这些矩阵用于确保深度学习模型能够正确地处理分子和材料在旋转下的对称性。

• CG系数（Clebsch-Gordan Coefficients）

  • 定义：Clebsch-Gordan系数是用于将两个角动量态合成一个总角动量态的系数。
  • 应用：在量子力学中，CG系数用于描述两个粒子的角动量如何合成，特别是在多粒子系统中。
  • 在几何深度学习中的应用：这些系数帮助模型处理和学习复杂的多体相互作用和角动量耦合。

• 径向模型（Radial Model）

  • 定义：径向模型描述了量子系统中径向部分的波函数，特别是对于中心势场系统（如原子）。
  • 应用：在量子力学中，径向模型用于分离薛定谔方程中的径向部分和角度部分，简化求解过程。
  • 在几何深度学习中的应用：径向模型帮助深度学习模型捕捉分子和材料的径向依赖性，从而更准确地预测量子性质。

球谐函数（Spherical harmonics）

---

球谐函数在几何深度学习中扮演着核心角色，它们通过提供一种强大的数学工具集，帮助研究者和开发者以更有效、更直观的方式处理和分析三维几何数据。球谐函数是定义在球面上的函数，在几何深度学习中的重要性主要体现在它们对于三维几何数据的分析和处理能力，尤其是在处理球面或球形几何结构时经常需要执行各种复杂的三维几何操作，如旋转、缩放和变形。球谐函数的数学特性使得这些操作可以以非常自然和数学上优雅的方式实现。

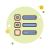
• 球坐标系$(r, \theta, \phi)$ 用于在空间中描述点的位置。其中, $r$ 表示径向距离, $\theta$ (天顶角)是从正 $z$ 轴向下的角度, 而 $\phi$ (方位角) 是在 $\mathrm{x}-\mathrm{y}$ 平面上从正 $x$ 轴测量的角度。

• 球谐函数在这种坐标系下定义, 能够有效描述球面上的复杂几何和物理过程。具体而言, 球坐标系与笛卡尔坐标系 $(x, y, z)$ 之间存在转换关系。给定球坐标中的点 $(r, \theta, \phi)$, 可以通过下列转换方程转换为笛卡尔坐标:
  $$
  \begin{cases}
  x=r \sin \theta \cos \phi \\
  y=r \sin \theta \sin \phi \\
  z=r \cos \theta
  \end{cases}
  $$

这种转换关系表明，虽然球谐函数本身在球坐标系下定义，描述球面上的点或者函数，它们也可以通过这种关系与笛卡尔坐标系中的点联系起来，从而在实际应用中描述3D空间中的物理现象或数学函数。

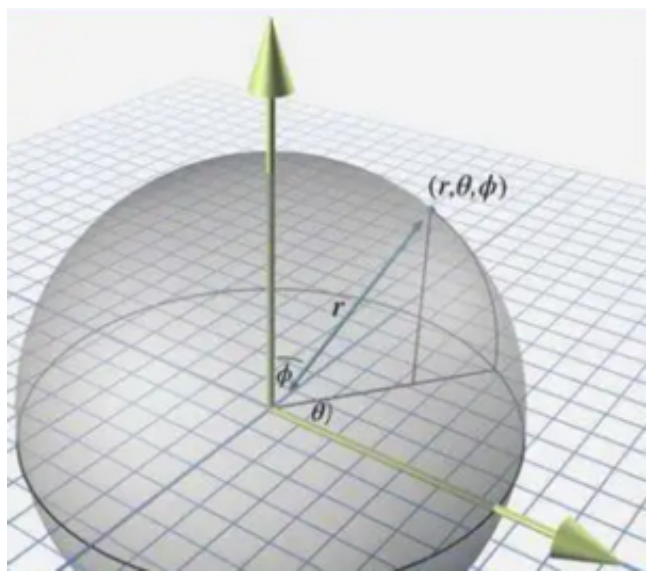
球谐函数类比泰勒公式

为例通俗的解释球谐函数的概念和应用，可以通过类比泰勒公式来帮助理解。泰勒级数是通过多项式的形式在某一点附近展开一个函数。这在一维或二维的平面上非常有效。具体来说，泰勒级数是基于函数在某一点处的导数信息来进行展开的，可以近似任何在该点处具有无限阶导数的函数。

泰勒级数的一般形式为:
$$
f(x)=f(a)+f^{\prime}(a)(x-a)+\frac{f^{\prime \prime}(a)}{2!}(x-a)^2+\frac{f^{\prime \prime \prime}(a)}{3!}(x-a)^3+\cdots
$$

球谐函数可以被看作是泰勒级数在球面上的一种推广。泰勒级数通过多项式的形式近似一个函数，在一维或二维平面上非常有效。而球谐函数则是在三维球面上对函数进行展开，从而实现类似的效果。不同的是，泰勒级数使用多项式作为基函数，而球谐函数使用的是定义在球面上的一组正交基函数。另一方面，泰勒级数主要用于一维或二维平面上函数的局部近似；球谐函数用于三维球面上的函数展开，类似对球面上函数的分解。

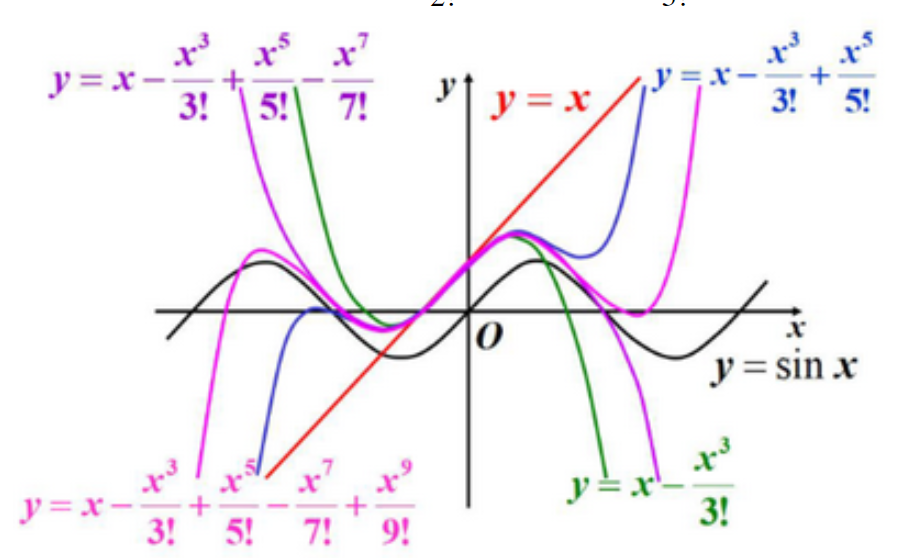
球谐函数类比傅里叶分解

傅里叶分解是将一个周期函数表示为一系列正弦和余弦函数（或指数函数）的和。傅里叶分解特别适用于处理周期性信号和函数。其形式为:
$$
f(x)=a_0+\sum_{n=1}^{\infty}\left(a_n \cos (n x)+b_n \sin (n x)\right)
$$

傅里叶分解的关键思想是利用一组正交基函数（正弦和余弦函数）来表示一个函数。

对比之前，两者都涉及使用一组正交基函数来表示一个函数的展开。傅里叶分解处理的是一维或二维的周期函数，而球谐函数处理的是三维球面上的函数。两者都基于正交基函数，通过展开来近似或表示复杂的函数。

球谐函数的定义

最后引出球谐函数的定义, 球谐函数是球坐标系中的解析函数, 通常表示为 $Y_l^m(\theta, \phi)$,其中 $l$ 是正整数, $m$ 是整数且 $-l \leq m \leq l$ 。这里, $\theta$ 是从正 $z$ 轴向下测量的天顶角, $\phi$ 是在 $\mathrm{xy}$ 平面上, 从正 $x$ 轴测量的方位角。

具体的, 球谐函数的一般形式是:
$$
Y_l^m(\theta, \phi)=P_l^m(\cos \theta) e^{i m \phi}
$$

其中, $P_l^m(\cos \theta)$ 是关联勒让德多项式, $e^{i m \phi}$ 是复指数函数, 表示旋转。 $l$ 称为球谐函数的阶, $m$ 称为次数。关联勒让德多项式 $P_l^m(x)$ 是勒让德多项式 $P_l(x)$ 的导数, 并乘以一个常数因子来满足正交性条件。它们可以通过罗德里格斯公式给出:
$$
P_l^m(x)=(-1)^m\left(1-x^2\right)^{m / 2} \frac{d^m}{d x^m} P_l(x)
$$

其中, $P_l(x)$ 是勒让德多项式, 可以通过罗德里格斯公式得到:
$$
P_l(x)=\frac{1}{2^l l!} \frac{d^l}{d x^l}\left(x^2-1\right)^l
$$

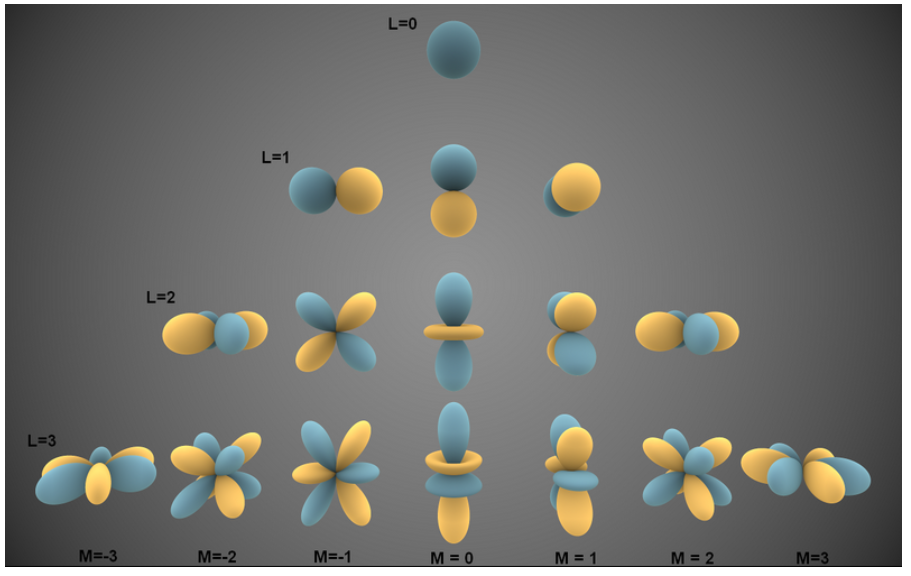
至于球谐函数的一般形式来源于勒让德多项式的推导，这里不做进一步的推导解释, 下面主要讲解其作用以及球谐函数公式中阶数 $l$ 和次数 $m$ 的代表的意义。如图所示, 是对球谐函数的参数 $l$ 和 $m$ 进行的可视化。

$$
泰勒公式：
\begin{aligned}
& f(x)=f(a)+f^{\prime}(a)(x-a)+\frac{f^{\prime \prime}(a)}{2!}(x-a)^2+\frac{f^{\prime \prime \prime}(a)}{3!}(x-a)^3+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n+ & \cdots
\end{aligned}
$$

为了方便理解l和m，可以考虑一个使用球谐函数拟合天体的场景

$l$ (阶数) 决定了大洲和大洋的“平面形状”复杂程度。

$m$次数决定大洲和大洋绕球面轴线（例如，北极到南极）的旋转对称性。换句话说，$m$决定了在绕天体一周时，大洲和大洋重复出现的次数。

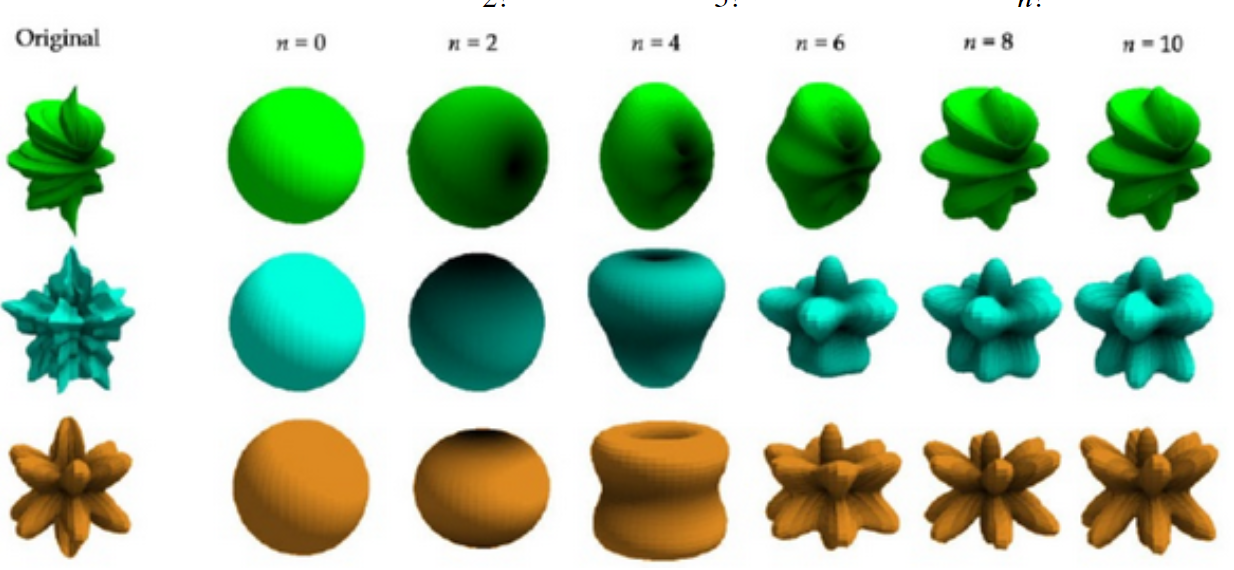
需要注意的是，一个球谐函数的描述都是在球面上的，“球面”意味着没有海拔信息。换句话说，如果这个天体的所有表面海拔都为0，那么一个球谐函数可以描述该天体表面大洲大洋的形状。如果想用球谐函数来模拟一个凹凸不平的立体天体，可以将球面上每一点的高度 $H(\theta, \phi)$ 表示为一系列球谐函数的加权和:
$$
H(\theta, \phi)=\sum_{l=0}^{\infty} \sum_{m=-l}^l a_{l m} Y_l^m(\theta, \phi)
$$

其中, $a_{l m}$ 是系数, 表示每个球谐函数在总高度分布中的权重。这实际上是通过不同阶和次的球谐函数线性组合来模拟高度变化。

球谐函数对称性讨论

• 在群论的教学中，我们讨论了群论中的对称性对几何数据的重要性，它往往作为几何深度学习模型的一种归纳偏置。而球谐函数在描述几何数据时展现出了一种特殊的性质：它们对三维空间中的旋转具有旋转不变性。这是因为球谐函数自身构成了球面上的一个正交基，为在旋转下仍能保持一致性的球面模式提供了一种自然的描述方式。

• 具体而言，在球面上应用SO(3)群中的任何旋转时，球谐函数的变换是可预测的。一个球谐函数旋转后，可以被表示为原始球谐函数集合的一个线性组合。这表明球谐函数能够以一种系统的方式捕获旋转操作的影响，而且这种影响可以通过分析原始函数的新组合来理解。这个特性使得球谐函数成为旋转群SO(3)的一个重要表示。

• 在数学上，表示是一种通过群的元素（本例中是旋转）来描述函数变换行为的方法。由于球谐函数在旋转下的这种可预测变换方式，我们可以使用它们作为一组基础工具，来描述和分析定义在球面上的任何函数。只要这个函数满足旋转对称性，即它的形态在旋转下保持不变或以可预测的方式变化，它就可以通过球谐函数的线性组合来表示。正如在一维空间中任何函数都可以通过傅立叶级数展开为正弦和余弦函数的线性组合一样，在球面上，函数也可以展开为球谐函数的线性组合。这个展开不仅包含了函数的空间分布，还隐含地编码了函数在旋转下的行为。 如果通过训练几何深度学习模型后，得到了球面函数对应的系数，就可以重建该函数在球面上的完整信息，包括它如何响应旋转变换。

• 综上所述，球谐函数中的l和m参数共同构成了一种系统化的方法，l提供了从粗糙到精细的多尺度视角，而m则提供了在每个尺度上沿方位角方向的细节和对称性。这种组合为几何形状和模式的识别、分类和分析提供了强大的工具，使得球谐函数在处理复杂球面数据，尤其是在几何深度学习领域中，成为了一个非常有价值的工具。

Winger D 矩阵（Winger D Matrix）

---

当我们对分子的空间位置进行建模，尤其是使用球谐函数时，我们需要考虑分子在不同方向上的行为。这包括分子的旋转以及如何描述旋转后的状态。Wigner D 矩阵在这一过程中起到了至关重要的作用。

阶数$l$是球谐函数 $Y_{l m}(\theta, \phi)$ 中的重要参数，对于一个固定的$l$ ，我们有一组 $2 l+1$ 个球谐函数，这些函数可以视为描述了分子的空间分布。

当分子旋转时，其电子分布或其他空间属性会随之变化。我们可以用旋转算符 $R(\alpha, \beta, \gamma)$ 来描述这种旋转，其中 $\alpha, \beta, \gamma$ 是欧拉角，表示绕不同轴的旋转。

Wigner $\mathrm{D}$ 矩阵 $D_{m^{\prime} m}^j(\alpha, \beta, \gamma)$ 是 $S O(3)$ 群的一个不可约表示。对于阶数$l$ ，可以使用 Wigner D 矩阵描述球谐函数在旋转下的变化。设 $|l, m\rangle$ 表示旋转行为，与之对应的球谐函数为 $Y_{l m}$ 。
在旋转 $R(\alpha, \beta, \gamma)$ 后，新的球谐函数可以表示为:
$$
R(\alpha, \beta, \gamma) Y_{l m}(\theta, \phi)=\sum_{m^{\prime}} D_{m^{\prime} m}^l(\alpha, \beta, \gamma) Y_{l m^{\prime}}\left(\theta^{\prime}, \phi^{\prime}\right)
$$

其中 $\theta^{\prime}$ 和 $\phi^{\prime}$ 是旋转后的角坐标。

Wigner $\mathrm{D}$ 矩阵 $D_{m^{\prime} m}^j(\alpha, \beta, \gamma)$ 描述了量子态在旋转下的变化。在神经网络中，Wigner D 矩阵可以用于确保特征在旋转操作下的转换。这意味着，如果输入数据旋转了，相应的特征也会按照 Wigner D 矩阵进行旋转变换，从而保持等变性。

具体来说：

• 旋转不变特征提取：通过将三维数据投影到球谐函数基上，得到的展开系数作为特征。这些特征在数据旋转时保持不变，可以用于分类、识别等任务。
• 旋转等变网络设计: 利用 Wigner D矩阵，在网络层之间传递旋转等变的特征。这种设计确保了网络在处理旋转数据时，输出会随着输入的旋转而相应地旋转。代码示例如下：

import numpy as np
from scipy.special import sph_harm

# 定义球谐函数
def compute_spherical_harmonics(l, m, theta, phi):
    return sph_harm(m, l, phi, theta)

from scipy.special import factorial

# 计算Wigner D矩阵
def wigner_d_matrix(j, alpha, beta, gamma):
    d_matrix = np.zeros((2 * j + 1, 2 * j + 1), dtype=complex)
    for mp in range(-j, j + 1):
        for m in range(-j, j + 1):
            d_matrix[mp + j, m + j] = np.exp(-1j * mp * alpha) * small_d(j, mp, m, beta) * np.exp(-1j * m * gamma)
    return d_matrix

def small_d(j, mp, m, beta):
    d = 0
    for k in range(int(max(0, m - mp)), int(min(j - mp, j + m)) + 1):
        d += ((-1) ** (m - mp + k) * np.sqrt(factorial(j + mp) * factorial(j - mp) * factorial(j + m) * factorial(j - m)) /
              (factorial(j - mp - k) * factorial(j + m - k) * factorial(k) * factorial(mp - m + k)) *
              np.cos(beta / 2) ** (2 * k + mp - m) * np.sin(beta / 2) ** (2 * j - 2 * k - mp + m))
    return d

# 示例: 计算 j = 1 的 Wigner D 矩阵
j = 1
alpha, beta, gamma = np.pi / 3, np.pi / 4, np.pi / 6
D_matrix = wigner_d_matrix(j, alpha, beta, gamma)
print("Wigner D 矩阵 (j = 1):\n", D_matrix)

Wigner D 矩阵 (j = 1):
 [[ 2.77555756e-17+0.14644661j  2.50000000e-01+0.4330127j
   7.39198920e-01+0.4267767j ]
 [-4.33012702e-01-0.25j       -7.07106781e-01+0.j
   4.33012702e-01-0.25j      ]
 [ 7.39198920e-01-0.4267767j  -2.50000000e-01+0.4330127j
   2.77555756e-17-0.14644661j]]

import torch
import torch.nn as nn

class EquivariantLayer(nn.Module):
    def __init__(self, j, alpha, beta, gamma):
        super(EquivariantLayer, self).__init__()
        self.j = j
        self.D_matrix = torch.tensor(wigner_d_matrix(j, alpha, beta, gamma), dtype=torch.cfloat)

    def forward(self, x):
        # 输入 x 的形状为 (batch_size, 2j + 1)
        return torch.matmul(x, self.D_matrix)

# 示例: 创建等变层并进行前向传播
j = 1
alpha, beta, gamma = np.pi / 3, np.pi / 4, np.pi / 6
equivariant_layer = EquivariantLayer(j, alpha, beta, gamma)

# 创建一个示例输入
x = torch.rand((1, 2 * j + 1), dtype=torch.cfloat)
print("输入:\n", x)

# 前向传播
output = equivariant_layer(x)
print("输出:\n", output)

输入:
 tensor([[0.4397+0.0432j, 0.4085+0.8599j, 0.6284+0.4830j]])
输出:
 tensor([[ 0.7023-0.3213j, -0.5639-0.2555j,  0.7692+0.3978j]])

为什么 Wigner-D 矩阵保证等变性？

在量子力学中，我们用数学工具来描述旋转。一个重要的工具就是 Wigner-D 矩阵。它告诉我们在量子世界里，当我们旋转一个物体时，量子态（可以理解为描述物体状态的数学对象）是如何变化的。

Wigner-D 矩阵是专门用来描述旋转的。就像你用一把尺子可以精确测量长度，Wigner-D 矩阵能精确描述旋转后的量子态。所有的旋转都可以用一套固定的数学规则描述，Wigner-D 矩阵遵循这些规则（SO3群不可约表示，欧拉角等）。这些规则确保了任何量子态在旋转后都能用同样的方式描述。当你用 Wigner-D 矩阵来旋转一个量子态时，它虽然会改变态的具体表达，但不会改变系统的物理性质。就像你把一个球旋转后，球上的点换了位置，但球的形状没变。

具体来说，假设你有一个量子态 $|\psi\rangle$ ，表示为一个向量。当你旋转这个态时，比如绕某个轴旋转，旋转后的态会变成一个新态 $\left|\psi^{\prime}\right\rangle$ 。这个新态可以用Wigner-D矩阵 $D$ 和原来的态 $|\psi\rangle$ 表示:
$$
\left|\psi^{\prime}\right\rangle=D|\psi\rangle
$$

这就像是你用一个函数 $f(x)$ 来描述一个球上的点，旋转后这些点变成 $f^{\prime}(x)$ ，但函数形式保持一样，只是输入 (点的位置) 变了。反之，如果旋转这个量子态而不使用 Wigner-D 矩阵，我们不能保证变换后的量子态 $\left|\psi^{\prime}\right\rangle$ 与原态 $|\psi\rangle$ 之间的关系满足旋转对称性的要求，比如用一个随意的矩阵 $M$ 来变换
$$
\left|\psi^{\prime}\right\rangle=M|\psi\rangle
$$

这种变换 $M$ 不一定满足旋转对称性的要求。换句话说，可能导致对象发生形变。从这个角度解释，Wigner-D 矩阵提供了一种严格的、标准化的等变性，即输入变了多少，输出就变了多少。而不用 Wigner-D 矩阵可能只能实现一种广义的、不严格的等变性，即输出也会随着输入的变换而变换，但这个变换尺度不一致，可能导致原物体的形变。因此，Wigner-D 矩阵在量子力学中的重要性在于它能够确保系统在旋转变换中的严格对称性和物理一致性。

CG系数（Clebsch-Gordan coefficients）

---

在上述内容中，我们知道，球谐函数可以表征几何空间中的对象形状和状态。基于球谐函数表示的不同对象之间的交互需要遵循球谐函数的一些性质，例如对称性和正交性。因此，这些对象之间的信息交互与融合不能直接使用常见的加法、乘法或求平均等常规操作，而是需要借助克莱布什-戈登（CG）系数。CG系数的使用确保特征耦合过程遵循球谐函数的对称性和正交性，从而最大限度地保留了原始信息的完整性和准确性。

具体来说，CG系数是将两个角动量（或更一般地，两个球谐函数）量子态的直接积 (tensor product)， 表示为不同总角动量量子态的线性组合的系数。假设我们有两个角动量 $l_1$ 和 $l_2$ ，以及对应的磁量子数 $m_1$ 和 $m_2$ ，则它们的直接积可以表示为:
$$
\left|l_1, m_1\right\rangle \otimes\left|l_2, m_2\right\rangle
$$

总角动量 $L$ 的态可以表示为:
$$
|L, M\rangle
$$

CG系数 $C_{l_1, m_1 ; l_2, m_2}^{L, M}$ 是满足下列关系的系数:
$$
\left|l_1, m_1\right\rangle \otimes\left|l_2, m_2\right\rangle=\sum_{L, M} C_{l_1, m_1 ; l_2, m_2}^{L, M}|L, M\rangle
$$
进一步的，CG系数满足正交性与对称性，即：

• 对称性1：交换 $l_1$ 和 $l_2$ 以及 $m_1$ 和 $m_2$ 的位置:
  $$
  C_{l_1, m_1 ; l_2, m_2}^{L, M}=C_{l_2, m_2 ; l_1, m_1}^{L, M}
  $$

• 对称性2: 改变 $m_1$ 和 $m_2$ 的正负符号，同时总角动量磁量子数 $M$ 也改变符号:
  $$
  C_{l_1, m_1 ; l_2, m_2}^{L, M}=(-1)^{l_1+l_2-L} C_{l_1,-m_1: l_2,-m_2}^{L,-M_2}
  $$

• 正交性1 对于固定的 $l_1, l_2, l$ 和不同的磁量子数组合 $m_1, m_2, M$ :
  $$
  \sum_{m_1, m_2} C_{l_1, m_1 ; l_2, m_2}^{l, M} C_{l_1, m_1 ; l_2, m_2}^{l^{\prime}, M^{\prime}}=\delta_{l, l^{\prime}} \delta_{M, M^{\prime}}
  $$

• 正交性2： 对于固定的 $l_1, l_2, m_1, m_2$ 和不同的总角动量组合 $l, M$ :
  $$
  \sum_{l, M} C_{l_1, m_1 ; l_2, m_2}^{l, M} C_{l_1, m_1^{\prime} ; l_2, m_2^{\prime}}^{l, M}=\delta_{m_1, m_1^{\prime}} \delta_{m_2, m_2^{\prime}}
  $$

正交性公式表明，对于固定的角动量 $l_1, l_2$ 和总角动量 $l$ ，不同的磁量子数组合 $m_1, m_2$ 的CG系数在内积时产生的结果是一个克罗内克 $\delta$ 函数。这意味着，当 $l$ 和 $M$ 不同时，内积为零 (它们是正交的）；当 $l=l^{\prime}$ 且 $M=M^{\prime}$ 时，内积为 1 (它们是标准化的)。换句话说，这个公式确保了不同总角动量态 $|l, M\rangle$ 在磁量子数组合 $\left|l_1, m_1\right\rangle \otimes\left|l_2, m_2\right\rangle$ 基底上的投影是正交且标准化的。M同理。

此外，CG系数还需要满足三角不等式这来源于角动量加法规则中的选择定则。具体来说，$\mathrm{CG}$ 系数只在 $\left|j_1-j_2\right| \leq j \leq j_1+j_2$ 时不为零，并且:$m=m_1+m_2$

CG系数的计算可以通过解析表达式或查表获得。一个典型的计算公式是:

$$
CG系数=\sqrt{2 s+1} \sum_k \frac{(-1)^k \sqrt{\left(s_1+s_2-s\right)!\left(s_1-s_2+s\right)!\left(s_2-s_1+s\right)!}}{\left(s_1+n_1-k\right)!\left(s_2+n_2-k\right)!\left(s-s_1-s_2+k\right)!k!}
$$

这里的 $k$ 是一个求和变量，其范围由每个项的阶乘部分的非负性决定。

在深度学习中，我们可以类比CG系数为特征融合过程中的一种权重系数。具体来说，在深度学习中，特征融合涉及将来自不同层或不同源的特征进行组合，以形成更具表达力的特征表示。类似于CG系数在角动量耦合中的作用，这些融合过程需要遵循一定的对称性和正交性原则，以确保信息融合的有效性。

对称性：在特征融合过程中，对称性可以类比为特征组合的顺序不影响最终结果。例如，结合图像特征和文本特征的多模态模型中，先处理图像特征再处理文本特征，或先处理文本特征再处理图像特征，都应得到相同的融合结果。

正交性：特征融合过程中的正交性确保不同特征在融合时不丢失各自的独立性，避免冗余信息的出现。正如CG系数确保不同角动量态之间的正交性，深度学习中的特征融合应尽量保持输入特征的独立性和互补性。

import sympy
from sympy.physics.quantum.cg import CG
from sympy import S

def clebsch_gordan(j1, m1, j2, m2, j, m):
    """
    计算克莱布什-戈登系数 C_{j1, m1 ; j2, m2}^{j, m}

    参数:
    j1, m1: 第一个角动量的量子数和磁量子数
    j2, m2: 第二个角动量的量子数和磁量子数
    j, m: 耦合后的总角动量的量子数和磁量子数
    """
    cg = CG(S(j1), S(m1), S(j2), S(m2), S(j), S(m)).doit()
    return float(cg)

# 示例计算
j1, m1 = 1, 1
j2, m2 = 1, -1
j, m = 1, 0
cg_coeff = clebsch_gordan(j1, m1, j2, m2, j, m) 

cg_coeff

0.7071067811865476

import numpy as np

def feature_fusion(feature1, feature2, cg_coeff):
    """
    特征融合函数，使用CG系数作为权重

    参数:
    feature1: 第一个特征向量（例如图像特征）
    feature2: 第二个特征向量（例如文本特征）
    cg_coeff: 计算得到的克莱布什-戈登系数
    """
    return cg_coeff * feature1 + (1 - cg_coeff) * feature2

# 示例特征
image_feature = np.array([1.0, 0.5, 0.2])
text_feature = np.array([0.3, 0.7, 0.9])

# 计算CG系数
cg_coeff = clebsch_gordan(1, 1, 1, -1, 1, 0)

# 特征融合
fused_feature = feature_fusion(image_feature, text_feature, cg_coeff)
print(f"融合特征: {fused_feature}")

融合特征: [0.79497475 0.55857864 0.40502525]

对于上述代码，简单解释一下cg_coeff × feature1 + (1 - cg_coeff) × feature2的作用。

首先，直接将两个特征简单相加可能会导致以下问题：

• 信息冗余：特征之间的相关性没有得到处理，可能会导致信息冗余，影响模型的效果。
• 权重不均衡：两个特征在实际应用中可能有不同的重要性，简单相加无法反映这一点。

因此CG系数本身的正交性可以避免交互时的信息冗余，因此在特征融合中，我们借用CG系数的概念，通过使用权重系数来确保不同特征的独立性，避免信息冗余。但是，仅通过线性组合的方式cg_coeff feature1 + (1 - cg_coeff) feature2 并不能完全保证正交性，它只是一个借鉴正交性思想的尝试。

import numpy as np
from sympy.physics.quantum.cg import CG
from sympy import S

def clebsch_gordan_coeff(l1, m1, l2, m2, l, m):
    """
    计算克莱布什-戈登系数 C_{l1, m1; l2, m2}^{l, m}
    """
    return float(CG(S(l1), S(m1), S(l2), S(m2), S(l), S(m)).doit())

def tensor_product_cg(V1, V2, W):
    """
    计算 CG 张量积
    参数:
    V1, V2: 输入特征矩阵，分别形如 (2*l1+1, C1) 和 (2*l2+1, C2)
    W: 可学习参数矩阵，形如 (C1, C2, C)

    返回:
    V: 输出特征矩阵，形如 (2*l+1, C)
    """
    l1, C1 = V1.shape
    l2, C2 = V2.shape
    l = (l1 - 1) // 2 + (l2 - 1) // 2
    V = np.zeros((2 * l + 1, W.shape[2]))
    # 通过多重循环遍历所有可能的特征维度和通道组合。
    for m in range(-l, l + 1):
        for c in range(W.shape[2]):
            for c1 in range(C1):
                for c2 in range(C2):
                    for m1 in range(-l1//2, l1//2 + 1):
                        for m2 in range(-l2//2, l2//2 + 1):
                            if abs(m1 + m2) <= l:
                                Q = clebsch_gordan_coeff(l1//2, m1, l2//2, m2, l, m)
                                V[m + l, c] += W[c1, c2, c] * Q * V1[m1 + l1//2, c1] * V2[m2 + l2//2, c2]
    return V

# 示例特征矩阵
V1 = np.random.rand(3, 4)  # l1=1, C1=4
V2 = np.random.rand(5, 6)  # l2=2, C2=6
W = np.ones((4, 6, 8))  # 可学习参数矩阵

# 计算 CG 张量积
V = tensor_product_cg(V1, V2, W)
print("CG 张量积结果: \n", V)

CG 张量积结果: 
 [[ 3.72821336  3.72821336  3.72821336  3.72821336  3.72821336  3.72821336
   3.72821336  3.72821336]
 [10.59200757 10.59200757 10.59200757 10.59200757 10.59200757 10.59200757
  10.59200757 10.59200757]
 [13.432774   13.432774   13.432774   13.432774   13.432774   13.432774
  13.432774   13.432774  ]
 [14.80095141 14.80095141 14.80095141 14.80095141 14.80095141 14.80095141
  14.80095141 14.80095141]
 [12.93742844 12.93742844 12.93742844 12.93742844 12.93742844 12.93742844
  12.93742844 12.93742844]
 [12.21554941 12.21554941 12.21554941 12.21554941 12.21554941 12.21554941
  12.21554941 12.21554941]
 [ 6.37701218  6.37701218  6.37701218  6.37701218  6.37701218  6.37701218
   6.37701218  6.37701218]]

1.$V_1$和$V_2$

由于 $V_1$ 代表的是角动量 $l_1$ 的特征，根据球谐函数，其特征维度数为m的取值范围： $2l_1 + 1 = 2 \times 1 + 1 = 3$，因此第一维度为3。C1=4 表示通道数 $C_1$ 为4，这是特征矩阵的第二维度，表示有4个通道。

同理，由于 $V2$ 代表的是角动量 $l_2$ 的特征，其特征维度数为 $2l_2 + 1 = 2 \times 2 + 1 = 5$，因此第一维度为5。C2=6 表示通道数 $C_2$ 为6。这是特征矩阵的第二维度，表示有6个通道。

2.输出结果 ' $V$ '

形状为 ' $(4,6,8)$ ' 的矩阵。

• $c_1=4$ ：对应 $v_1$ 的4个通道。
• $c_2=6$ ：对应 $v_2$ 的6个通道。
• c=8 : 表示输出的 8 个通道。

在函数tensor_product_cg中，计算得到的输出特征矩阵 V 的形状为 $(2l + 1, C)$。

其中$l = (l1 + l2) = 1 + 2 = 3$ ，因此输出特征矩阵的第一个维度为 $2l + 1 = 2 \times 3 + 1 = 7$。
输出特征矩阵 V 的形状为 (7, 8)，表示有7个特征维度和8个通道。

3.可学习参数矩阵 ' $w$ '

$W[c_1, c_2, c]$：
$W$ 是可学习的参数矩阵，其维度为 $(C1, C2, C)$。
$c_1$ 和 $c_2$ 分别表示 $V_1$ 和 $V_2$ 的通道索引，$c$ 表示输出通道索引。
$W[c1, c2, c]$ 表示从 $c_1$ 和 $c_2$ 通道映射到 $c$ 通道的权重参数。

4.CG系数 Q'

Q是CG系数，$Q \cdot V 1 \cdot V 2$确保了只有在特定角动量$l$耦合规则下（对称性，正交性，三角不等式），特征才能进行有效的交互和融合（不符合角动量$l$耦合规则时，Q为0），从而避免了不相关特征之间的相互干扰。

径向模型（Radial Model）

---

在极坐标的背景下, 结合之前关于球谐函数的讲解, 可以发现其只能表征球坐标系下的极角 $\theta$ 和方位角 $\phi$ 信息。其公式表示也可以证明这一点: $Y_l^m(\theta, \phi)$ 。

因此, 如果想对极坐标系下全部的物理量 (距离 $r$, 极角 $\theta$ 和方位角 $\phi$ ) 进行完整的描述，这里还需要一个表征距离的数学模型，即径向模型。这是一种用于分析或描述空间对象（如分子、原子、粒子或天体）中心向外延展特性的数学模型，用于理解和预测对象的行为和性质。径向模型的关键在于它提供了一种简化但强大的方式来分析和理解具有球形对称性或近似对称性系统的物理性质。通过将复杂的三维问题简化为一维问题（空间分布简化为距离表示），研究人员可以更容易地获得系统性质的深入洞见，并开发出准确的理论模型和数值模拟方法。

径向模型通常涉及一个或多个径向函数，这些函数表达了某个或某些物理量如何随着距离中心点的距离而变化。这种描述可以是简单的解析函数，也可以是复杂的数值模型，具体取决于研究对象的性质和所需的精确度。一个常见的径向函数为高斯径向函数。

先通俗的理解一些高斯径向函数的作用。想象量子力学的场景，每个原子或分子都被一团云雾包围，这团云雾代表着电荷的分布。在现实世界中，电荷并不是集中在一个点上，而是分布在一个区域内。高斯径向函数就是用来描述这种“云雾”或电荷分布的数学工具。这种云雾的形状类似于高斯函数这种钟形曲线，它在原子或分子的中心最密集，向外扩散时逐渐变得稀疏。

现在，当我们谈论两个原子或分子之间的相互作用时，可以想象它们各自的云雾开始相互重叠。高斯镜像函数帮助我们计算这种重叠的程度，从而了解原子之间的吸引或排斥力大小。通过分析这些云雾（即电荷分布）如何随着距离变化而改变，我们可以建立一个模型来描述这种相互作用的强度。
现在我们来看看高斯径向函数的数学形式。

高斯函数的一般形式为 $G(r)=A \exp \left(-\alpha r^2\right)$, 其中 $r$ 是从电荷分布中心到某点的距离, $A$是振幅（或高度）系数, 而 $\alpha$ 是一个正常数, 控制着高斯函数的宽度或扩散程度。

$A$ 在当前场景下可以看作电荷分布总量。

• $\alpha$ 值越大：当 $\alpha$ 的值增大时, $-\alpha r^2$ 的值（对于任何给定的 $r>0$ ）会变得更负, 使得 $\exp \left(-\alpha r^2\right)$ 这部分快速趋近于零。这意味着电荷分布迅速随距离减小, 导致电荷主要集中在中心附近, 形成一个更 “尖锐” 和集中的分布。

• $\alpha$ 值越小：相反，当 $\alpha$ 较小时, $-\alpha r^2$ 的负值减小, 使得 $\exp \left(-\alpha r^2\right)$ 这部分下降得更慢,电荷分布在空间中更加 “扁平” 和分散。

$r^2$ 是距离的平方, 是高斯函数中确保电荷分布对称性的关键部分。这里的 $r$ 表示从电荷分布的中心 (通常是原子核或分子的中心) 到分布外任意点的直线距离。由于 $r^2$ 同时考虑了所有方向上的距离（无论是 $\mathrm{x} 、 \mathrm{y}$ 还是 $\mathrm{z}$ 方向）, 它确保了分布的球形对称性一一无论观察点在中心点的哪个方向上, 只要距离相等, 电荷分布的密度就相同。

简而言之, $r^2$ 确保了电荷分布不依赖于方向, 只依赖于与中心的径向距离, 从而创造了一个完美的球形对称分布。这种对称性是分析和计算电荷分布及其相互作用时非常重要的特性，因为它简化了数学表达式，同时提供了对物理现象的直观理解。

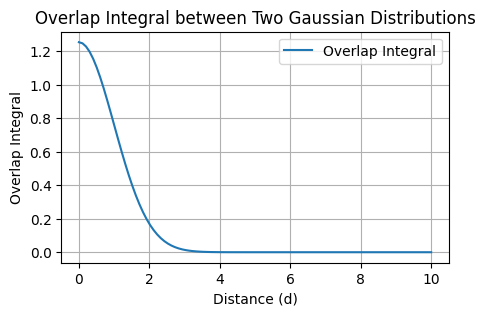
当我们考虑两个电荷分布（例如，两个原子或分子）之间的相互作用时，我们会计算这两个高斯函数的重叠部分。这种重叠部分的计算涉及到对两个高斯函数的乘积进行积分，最终给出了一个描述相互作用能量随距离变化的函数。这就是所谓的径向模型，它能帮助我们了解在不同距离下，这些原子或分子之间的相互作用强度如何变化，如下所示：

定义$G_1(r)$ 和 $G_2(r)$ 的重叠积分公式如下:
$$
I=\int_{-\infty}^{\infty} G_1(r) G_2(r) d r
$$

其中，假设两个高斯函数具有相同的形式，但中心位置不同:
$$
\begin{aligned}
& G_1(r)=A_1 \exp \left(-\alpha_1 r^2\right) \\
& G_2(r)=A_2 \exp \left(-\alpha_2(r-d)^2\right)
\end{aligned}
$$

这里， $d$ 是两个高斯分布中心之间的距离。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad

# 定义两个高斯函数
def G1(r, A1, alpha1):
    return A1 * np.exp(-alpha1 * r**2)

def G2(r, A2, alpha2, d):
    return A2 * np.exp(-alpha2 * (r - d)**2)

# 定义重叠积分的被积函数
def integrand(r, A1, alpha1, A2, alpha2, d):
    return G1(r, A1, alpha1) * G2(r, A2, alpha2, d)

# 设置参数
A1 = 1.0
alpha1 = 1.0
A2 = 1.0
alpha2 = 1.0

# 计算不同距离下的重叠积分
distances = np.linspace(0, 10, 100)
overlaps = []

for d in distances:
    result, error = quad(integrand, -np.inf, np.inf, args=(A1, alpha1, A2, alpha2, d))
    overlaps.append(result)

# 可视化结果
plt.figure(figsize=(5, 3))
plt.plot(distances, overlaps, label='Overlap Integral')
plt.xlabel('Distance (d)')
plt.ylabel('Overlap Integral')
plt.title('Overlap Integral between Two Gaussian Distributions')
plt.legend()
plt.grid(True)
plt.show()

除了高斯函数外，贝塞尔函数也经常被用于径向模型的建模。贝塞尔方程的一般形式是：

$$
x^2 \frac{d^2 y}{d x^2}+x \frac{d y}{d x}+\left(x^2-n^2\right) y=0
$$

其中:

• $y$ 是我们想要求解的函数, 依赖于变量 $x$ 。
• $n$ 是一个实数或整数, 称为贝塞尔方程的阶数, 与系统的对称性和问题的边界条件有关。
• 方程的左侧前两项代表了径向函数的导数, 而第三项包含了 $x^2$ 和 $n^2$, 提供了随着 $x$ 的变化而振荡的函数形式。

贝塞尔方程的解, 即贝塞尔函数, 通常表示为 $J_n(x)$ 和 $Y_n(x)$, 分别对应第一类和第二类贝塞尔函数:

• 第一类贝赛尔函数 $J_n(x)$ : 在 $x=0$ 时通常是有界的, 因此对于描述那些在原点附近行为良好的物理系统尤为重要。
• 第二类贝赛尔函数 $Y_n(x)$ : 在 $x=0$ 时是无界的, 适合于描述原点之外的区域。

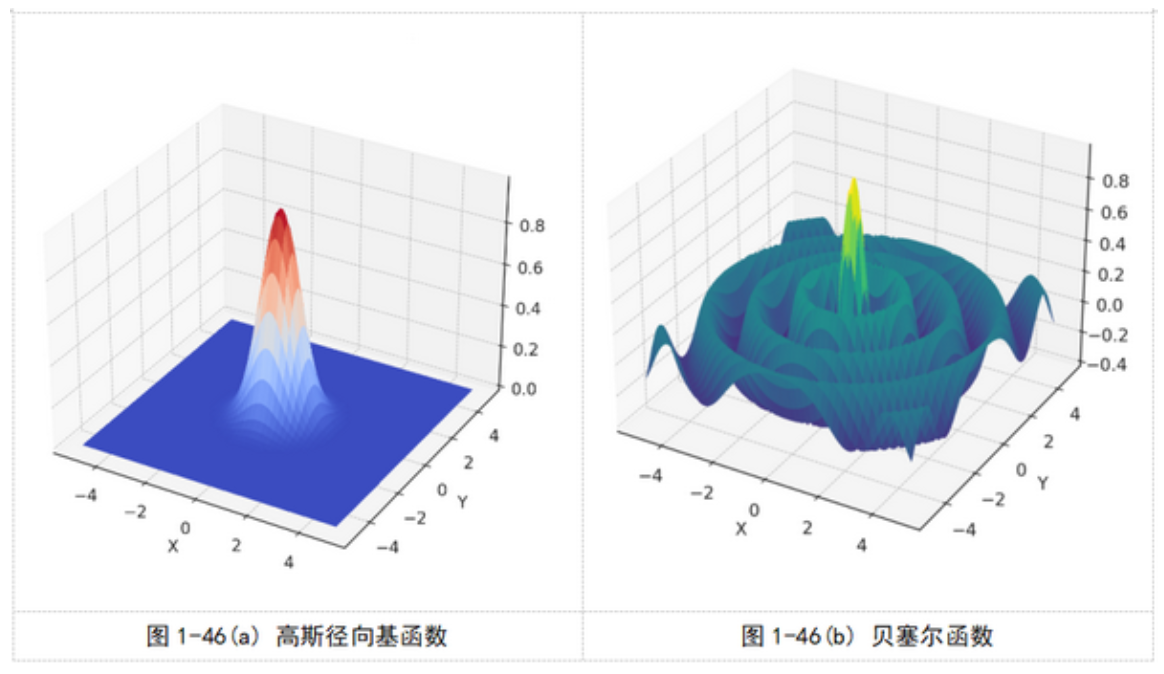
其中，第一类贝塞尔函数，在三维空间中形成了随着距离增加而出现振荡衰减的特性曲面。这种振荡衰减的行为适合于描述波动和振动等物理现象，以及一些复杂的分子间的相互作用。在处理具有特定对称性的物理问题时更为常见，如在分子动力学模拟和电磁场计算中，其中需要准确描述波动和振动现象。如下图所示：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
from scipy.special import iv  # Importing the modified Bessel function of the first kind

# 定义两个贝塞尔函数径向分布
def Bessel1(r, A1, alpha1):
    return A1 * iv(0, alpha1 * r)

def Bessel2(r, A2, alpha2, d):
    return A2 * iv(0, alpha2 * np.abs(r - d))

# 定义重叠积分的被积函数
def integrand(r, A1, alpha1, A2, alpha2, d):
    return Bessel1(r, A1, alpha1) * Bessel2(r, A2, alpha2, d)

# 设置参数
A1 = 1.0
alpha1 = 0.5
A2 = 1.0
alpha2 = 0.5

# 计算不同距离下的重叠积分
distances = np.linspace(0, 5, 100)
overlaps = []

for d in distances:
    result, error = quad(integrand, 0, 10, args=(A1, alpha1, A2, alpha2, d))  # 将积分区间限制在 [0, 10]
    overlaps.append(result)

# 可视化结果
plt.figure(figsize=(10, 6))
plt.plot(distances, overlaps, label='Overlap Integral')
plt.xlabel('Distance (d)')
plt.ylabel('Overlap Integral')
plt.title('Overlap Integral between Two Radial Bessel Distributions')
plt.legend()
plt.grid(True)
plt.show()

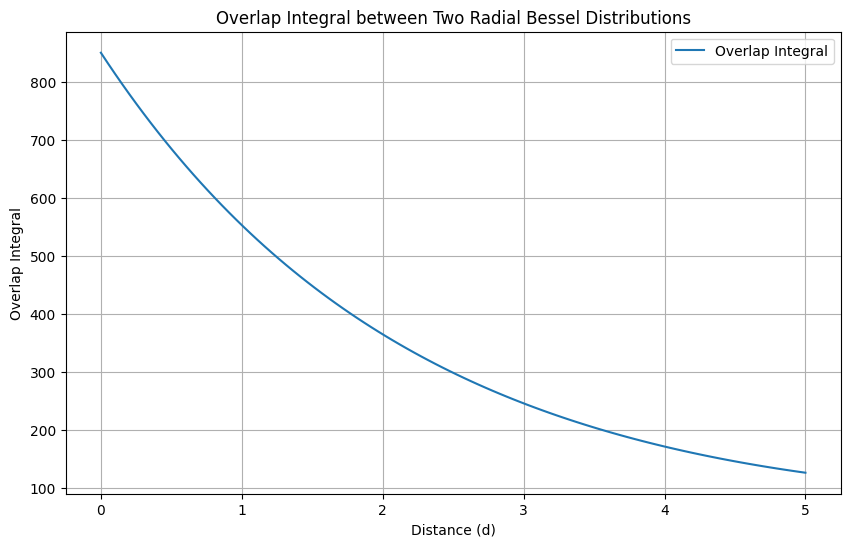
贝塞尔函数特别是零阶修正贝塞尔函数（Modified Bessel function of the first kind）通常在径向分布中表现为单调递增或单调递减，而不是震荡性质。若需要体现震荡性质，可以使用贝塞尔函数的另一种形式——例如，第一类第一种贝塞尔函数（Bessel function of the first kind）

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
from scipy.special import jv  # Importing the Bessel function of the first kind

# 定义两个贝塞尔函数径向分布
def Bessel1(r, A1, alpha1):
    return A1 * jv(0, alpha1 * r)

def Bessel2(r, A2, alpha2, d):
    return A2 * jv(0, alpha2 * np.abs(r - d))

# 定义重叠积分的被积函数
def integrand(r, A1, alpha1, A2, alpha2, d):
    return Bessel1(r, A1, alpha1) * Bessel2(r, A2, alpha2, d)

# 设置参数
A1 = 1.0
alpha1 = 2.0  # 适当调整以体现震荡性质
A2 = 1.0
alpha2 = 2.0  # 适当调整以体现震荡性质

# 计算不同距离下的重叠积分
distances = np.linspace(0, 20, 200)
overlaps = []

for d in distances:
    result, error = quad(integrand, 0, 10, args=(A1, alpha1, A2, alpha2, d))  # 将积分区间限制在 [0, 10]
    overlaps.append(result)

# 可视化结果
plt.figure(figsize=(10, 6))
plt.plot(distances, overlaps, label='Overlap Integral')
plt.xlabel('Distance (d)')
plt.ylabel('Overlap Integral')
plt.title('Overlap Integral between Two Radial Bessel Distributions')
plt.legend()
plt.grid(True)
plt.show()

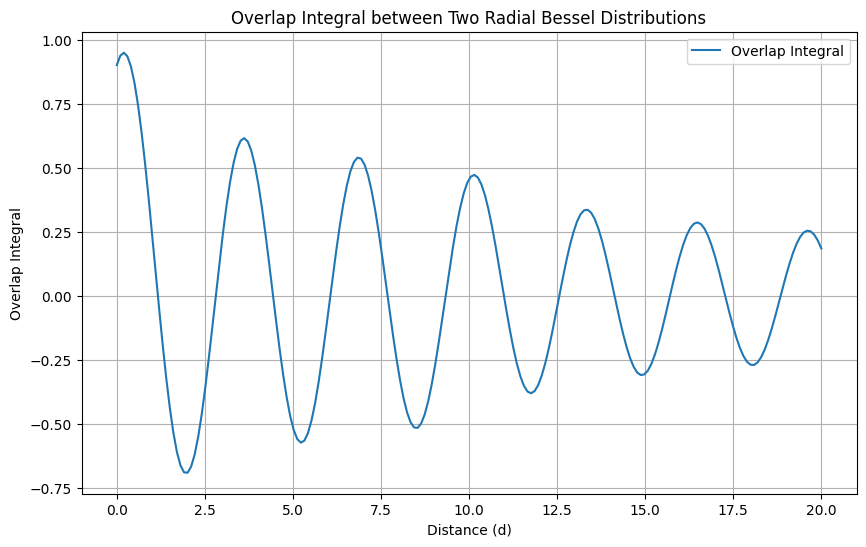
对比之下，高斯RBF具有以下特性：

1. 非局部性：虽然高斯函数随距离增加而迅速衰减，但理论上它在所有距离上都不为零，这意味着每个点都在一定程度上影响着整个空间。
2. 平滑性：高斯函数是光滑的，这使得它在机器学习和插值问题中特别有用，因为它可以产生平滑的曲面。

在径向模型中使用的第一类贝塞尔函数，具有以下特性：

1. 振荡性：与高斯函数不同，贝塞尔函数随着距离的增加表现出振荡性质，这反映了在某些物理系统中，如波动和振动系统，能量或信息的传递并非单调衰减。
2. 周期性：由于其振荡特性，贝塞尔函数特别适用于描述圆形或圆柱对称问题中的振荡现象，例如在声学、电磁学和流体力学中的波动问题。

在量子力学中，原子和分子的波函数通常在球坐标系下解决，特别是对于具有球形或圆柱形对称性的系统。贝塞尔函数可以用作波函数的径向部分，描述电子相对于原子核的概率分布。这种概率分布的“振荡”对于理解化学键的形成、电子的排布以及原子和分子的稳定性至关重要。

总的来说，一般形式地径向基函数可以定义为：
$$
\Phi(x, c)=\Phi(|x-c|)
$$

其中, $x$ 代表空间中的任意点, $c$ 是径向基函数的中心点, $|x-c|$ 表示 $x$ 与 $c$ 之间的距离。这里的距离可以是欧几里得距离, 也可以是非欧几里得空间中的其他合适的距离度量。
对于欧几里得空间中最常用的径向基函数——高斯核函数, 其形式可以特别表示为:
$$
k(|x-c|)=\exp \left(-\frac{|x-c|^2}{2 \sigma^2}\right)
$$

其中, $\sigma$ 是一个参数, 决定了函数的宽度, 即影响范围的大小; $|x-c|^2$ 表示 $x$ 与中心点 $c$ 之间距离的平方。

对于非欧几里得空间，距离需要根据该空间的几何特性来定义，可能涉及更复杂的距离计算方法。无论哪种空间，径向基函数的核心思想是保持不变的，即其值仅取决于计算点与参照点（一般为中心的）的相对距离，这使得它们在多种领域内，如插值、函数逼近、机器学习等，都有着广泛的应用。

8. 球谐函数与径向模型在DL中的结合

球谐函数和径向模型在几何深度学习中的结合主要体现在两方面：

• 数据预处理
• 模型的特征融合。

在数据预处理阶段，球谐函数用于对几何结构的频域特征进行提取。具体来说，首先将数据从笛卡尔坐标系（xyz）转换到球坐标系，得到每个点的径向距离、俯仰角和方位角。然后，基于俯仰角和方位角，可以利用球谐函数对球面上的数据进行展开。这个过程可以看作是在球面上对函数进行一系列的频域分解，类似于傅里叶变换在时间序列上的应用。每个球谐函数都可以捕获特定频率的空间变化，从而对复杂的三维形状进行编码。通过球谐展开，我们可以得到一系列由球谐基函数加权组合得到的函数表示，函数中的系数则描述了三维形状在不同空间频率上的特征。这些系数构成了形状的一个紧凑而全面的特征表示，可用于后续的学习任务。

径向模型则基于径向距离提取点的距离特征，这在处理局部结构和形状时特别有效。首先，计算径向模型时，数据中的中心点选择可以是随机选择的，也可以是基于某种准则（如最远点采样）选定的点。然后，对于每个中心点，计算其他点到此中心点的距离。最后，应用径向基函数，这通常是一个衰减函数，如高斯函数，将距离转换为对应特征的权重值。这样，每个点对于每个中心点都有不同的权重，反映了它在空间中相对于该中心点的位置和分布。

将球谐函数和径向模型提取的特征进行整合，形成一个统一的特征向量，作为几何深度学习模型的输入信息。值得注意的是，这些特征向量的一个关键属性是它们对三维形状的旋转是不变的，因为球谐系数的旋转可以通过Wigner-D小矩阵来实现。这种旋转不变性对于许多三维几何深度学习任务至关重要，它允许模型识别和理解经过旋转的物体或场景，而不会损失性能。当然，也可以将球谐函数和径向模型提取的特征分别作为模型的输入，这取决于不同模型的设计结构，将在第四章展开讲解。

另一方面，在几何图神经网络模型的特征聚合阶段，执行连续性卷积时（详见2.3章节），节点可以聚合其邻居的特征，权重由径向模型确定。这种基于距离的加权聚合可以帮助模型捕获空间结构和点之间的相对位置信息。

总结而言，球谐函数和径向模型在几何深度学习中的结合为几何数据的分析和识别提供了一个强大的框架。球谐函数捕获空间变化的特征，为复杂三维形状提供了一种紧凑而全面的表示。径向模型则补充了球谐函数的表示，通过测量点与中心点之间的距离来提取局部结构特征，增强了对形状细节的理解。特征融合进一步强化了这一过程，利用径向模型确定局部特征的加权聚合，进一步促进了模型对空间结构和点间相对位置信息的捕获，从而获得更好的模型性能。