在

AI数学基础

Deep Learning Math

高等数学（Advanced Mathematics）

高等数学在深度学习中起着关键作用。微积分的基础，如积分和微分，帮助我们理解模型的训练过程。通过导数和函数的单调性，我们可以判断模型的优化方向，并使用链式法则计算复杂函数的梯度。梯度下降法是深度学习优化的核心，通过计算梯度来最小化损失函数。函数的极值与鞍点、海森矩阵、以及函数的凹凸性可以帮助我们理解模型在优化过程中的行为和稳定性。此外，泰勒公式和傅里叶级数则用于函数的近似和信号处理，这在构建和优化复杂神经网络模型时尤为重要。通过这些数学工具，深度学习模型能够更有效地训练和优化，从而提高其性能和准确性。

Agenda

微积分 (Calculus)
- 积分 (Integration)
- 微分和导数 (Differentiation and Derivatives)
- 函数单调性(Monotonicity of Functions)
- 函数极值与鞍点(Extrema and Saddle Points of Functions)
- 海森矩阵（Hessian Matrix）
- 函数凹凸性(Concavity and Convexity of Functions)
链式法则 (Chain Rule)
梯度 (Gradient)
泰勒公式(Taylor Series/Taylor Expansion)
傅里叶级数（Fourier Series）

微积分

微积分是数学的一个分支，主要研究变化的量和它们之间的关系。微积分包括两个主要部分：微分学和积分学。

微分学侧重于研究函数的变化率和斜率，主要工具是导数，它能够描述瞬时变化的速度。
积分学则关注累积量，主要工具是积分，用于计算面积、体积及其他累积量。

积分（integration）

积分的几何解释是：该函数曲线下的面积。
积分的物理解释是：积分的物理意义随不同物理量而不同，比如对力在时间上积分就是某段时间内力的冲量；如果是对力在空间上的积分就是某段位移里力做的功。
积分的代数解释是：更精细的乘法运算。

这里如何理解积分是更精细的乘法运算？还是放到路程速度时间这个物理系统中举子：

假设现在速度 $v=5 \mathrm{~m} / \mathrm{s}$ 、时间 $t=10 \mathrm{~s}$, 行驶距离 $s$ 怎么求?

很简单正常的乘法即可处理 $(s=v t)$ 。但是有个前提, 即速度是恒定的。

那如果是变速的呢? 这就是积分的内容了。

假设现在的速度 $v=2 t$, 求第 10 时刻行驶过的路程?

积分的思想是将时间段尽可能的切分成小段, 以每一小段起始时刻的瞬时速度作为这一小段时间内的平均速度, 最后把这些小段时间内各自形式的路程加起来就是 10 秒内行驶的总路程,

具体解法如下:

$1 \mathrm{~s}$ 时, 小汽车的速度 $v_1=2 t=2 \cdot 1=2(\mathrm{~m} / \mathrm{s}) ;$
$2 \mathrm{~s}$ 时, 小汽车的速度 $v_2=2 t=2 \cdot 2=4(\mathrm{~m} / \mathrm{s})$;
$3 \mathrm{~s}$ 时, 小汽车的速度 $v_3=2 t=2 \cdot 3=6(\mathrm{~m} / \mathrm{s})$;
依次算下去,
$10 \mathrm{~s}$ 时, 小汽车的速度 $v_{10}=2 t=2 \cdot 10=20(\mathrm{~m} / \mathrm{s})$ 。
再用乘法运算计算出每一小段时间 $(t=1 \mathrm{~s})$ 的距离, 即:

$$
\begin{aligned}
s & =\sum_{i=1}^{10} s_i \\
& =s_1+s_2+s_3+\cdots+s_{10} \\
& =2+4+6+\cdots+20 \\
& =\frac{10(2+20)}{2} \\
& =110
\end{aligned}
$$

上面公式中，将10秒钟以一秒为间隔切分成10个小段时间，最后求得的路程是110m ，可视化图片如下所示。

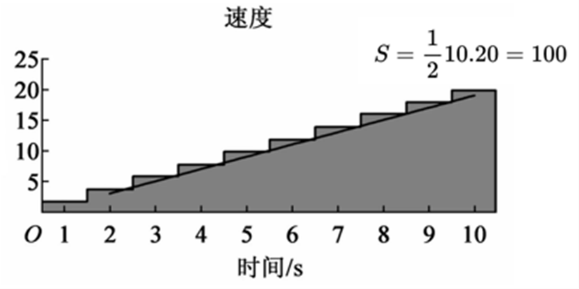
可以想象，当时间间隔足够小时，这个速度函数图像近似三角形，此时的路程就是这个三角形的面积等于100m，刚刚近似求得的110m离这个正确答案已经非常接近了。

所以积分的本质就是更精细的乘法，最后求和就可以得到输出结果了。

在深度学习领域，积分的运用远远没有微分多，因此这是只做简短的概念性的介绍。下面注重讲解微分。

微分和导数

微分（differential）和导数（derivative）都与函数的变化率有关，它们是两个相关但不完全相同的概念。首先一起深入了解这两者的定义和区别。

导数描述了一个函数在某一点上的切线斜率。如果有一个函数 $y=f(x)$, 则其在点 $x$处的导数通常表示为 $f^{\prime}(x)$ 或 $\frac{\mathrm{d} y}{\mathrm{~d} x}$ 。导数的定义是函数在该点的平均变化率的极限, 公式如下:
$$
f^{\prime}(x)=\lim _{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}
$$
微分描述了函数值的微小变化与自变量的微小变化之间的关系。对于函数 $y=f(x)$, 它的微分表示为 $\mathrm{d} y$ 和 $\mathrm{d} x$, 其中 $\mathrm{d} y$ 是函数值的微小变化, 而 $\mathrm{d} x$ 是自变量的微小变化。微分的定义基于导数, 可以表示为:
$$
\mathrm{d} y=f^{\prime}(x) \cdot \mathrm{d} x
$$

所以，导数和微分都与函数的变化率有关，但它们的重点略有不同。导数关注的是函数在某点的切线斜率，而微分关注的是函数值的微小变化与自变量的微小变化之间的关系。

简言之，导数是一个比率或斜率的概念，而微分描述了当自变量发生微小变化时，因变量如何变化。

导数的精细的除法

导数的几何解释是：该函数曲线在这一点上的切线斜率。
导数的物理解释是：导数物理意义随不同物理量而不同,但都是该量的变化的快慢函数，即变化率。
导数的代数解释是：更精细的除法运算。

前两个解释的角度相信读者已经很熟悉了，那么怎么理解导数的代数是更精细的除法运算这一说法呢？

举一个物理例子:

距离 $s=25 \mathrm{~m}$, 时间 $t=5 \mathrm{~s}$, 求平均速度 $v$ ?

这个问题很好回答, 正常的除法即可轻松处理 ( $v=s / t)$ 。

但是如果速度不是均速, 而且希望求得第 5 秒时的瞬时速度, 怎么办?
$$
v=\left.\frac{\mathrm{d} s}{\mathrm{~d} t}\right|_{t=5}=\lim _{\Delta t \rightarrow 0} \frac{s(5+\Delta t)-s(5)}{\Delta t}
$$

$\Delta t$ 是一个很多的时段, 用 $(5+\Delta t)$ 时刻走过的路程 $s(5+\Delta t)$ 减去第五秒时走过的路程 $s(5)$, 再除以时段 $\Delta t$, 解得的就是第五秒时的瞬时速度。当 $\Delta t$ 无穷小时, 就是导数的概念了, 即 $\lim _{\Delta t \rightarrow 0} \frac{s(5+\Delta t)-s(5)}{\Delta t}$ 。

可以看出来导数是即时的变化率, 放在路程和时间这个物理场景下, 瞬时速度就是路程的即时变化率。其求解的方法就是一个简单的除法而已！本质上还是除法运算。

导数的解读

回忆一下微分的数学表达式:
$$
\frac{\mathrm{d} y}{\mathrm{~d} x}=f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}
$$

导数含义的解读:

导数揭示了函数 $f(x)$ 在某点的切线斜率。
导数揭示了函数 $f(x)$ 在某点的变动规律。

在这里我更推崇第二种解读方法。其实可以把 $\mathrm{d} x$ 乘到等号右边去会更形象, 即:

$$
\begin{gathered}
\frac{\mathrm{d} y}{\mathrm{~d} x}=f^{\prime}(x) \\
\mathrm{d} y=f^{\prime}(x) \mathrm{d} x
\end{gathered}
$$

举个例子来解读什么叫函数 $f(x)$ 在某点的变动规律。假设 $f(x)=x^2$, 求 $x=5$ 处的导数。
$$
\frac{\mathrm{d} y}{\mathrm{~d} x}=2 x=10 \quad \mathrm{~d} y=10 \mathrm{~d} x
$$
即, 变量 $x$ 变动一点点, 将引起函数 $f(x)$ 值相对于变量 $x$ 十倍的变化。这点很重要。

可以根据这个解读来推导一下微分的乘法法则和幂法则。举一个例子, 假设函数 $h(x)=f(x) \cdot g(x)$, 先回忆一下微分的乘法法则:
$$
h^{\prime}(x)=\frac{\mathrm{d} h}{\mathrm{~d} x}=\frac{\mathrm{d} f}{\mathrm{~d} x} g(x)+f(x) \frac{\mathrm{d} g}{\mathrm{~d} x}=f^{\prime} g+f g^{\prime}
$$

下面来推导一下乘法法则怎么来的。

首先, 把函数 $h(x)=f(x) \cdot g(x)$ 放在求解矩形面积这个例子中, 即 $h(x)$ 是矩形面积、 $f(x)$ 是宽、 $g(x)$ 是高, 此时当变量 $x$ 变动一点点时, 根据微分的解读, 其意义是矩形面积的变动率，如下图

其中 $\mathrm{d} h$ 为面积的变动, 即图中蓝色的部分: $\mathrm{d} h=\mathrm{d} f \cdot g(x)+f(x) \cdot \mathrm{d} g+\mathrm{d} f \cdot \mathrm{d} g$,
由于 $\mathrm{d} f \cdot \mathrm{d} g$ 是二阶无穷小, 约等于 0 , 可以约掉;
再在等号左右分别除去 $\mathrm{d} x$ 就得到了微分的乘法法则 $\frac{\mathrm{d} h}{\mathrm{~d} x}=\frac{\mathrm{d} f}{\mathrm{~d} x} g(x)+f(x) \frac{\mathrm{d} g}{\mathrm{~d} x}$ 。
此时, $\mathrm{d} h$ 为面积的变动, 而 $\frac{\mathrm{d} h}{\mathrm{~d} x}$ 为面积的变动率。

同理，可以继续推导导数的幂法则：

$$
\frac{\mathrm{d}\left(x^n\right)}{\mathrm{d} x}=n x^{n-1}
$$

还用刚刚的例子, 如果此时 $f(x)$ 和 $g(x)$ 都等于 $x$, 那么 $h(x)=x^2, \mathrm{~d} h=\mathrm{d} x^2$, 如下图所示。

此时正方形面积的变动根据公式推导如下:
$$
\mathrm{d} h=x \cdot \mathrm{d} x+x \cdot \mathrm{d} x+\mathrm{d} x \cdot \mathrm{d} x=2 x \mathrm{~d} x
$$

因为 $\mathrm{d} h=\mathrm{d} x^2$, 代入整理得到 $\frac{\mathrm{d} x^2}{\mathrm{~d} x}=2 x$ 。

这个推导结果与直接使用幂法则 $\mathrm{d} h=\mathrm{d} x^2=2 x$ 求得的结果是一致的。

同样的方法推广到三维空间, 乘法法则和幂法则的推导也是适用的, 如图:

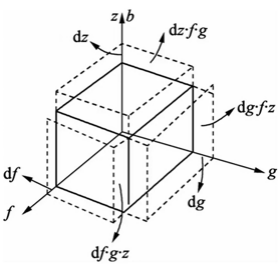
此时的体积计算公式为 $y=f(x) \cdot g(x) \cdot z(x)$, 体积的变动为:
$$
\mathrm{d} y=\mathrm{d} f \cdot g \cdot z+\mathrm{d} g \cdot f \cdot z+\mathrm{d} z \cdot f \cdot g
$$

如果此时 $f(x) 、 g(x)$ 和 $z(x)$ 都等于 $x$, 那么体积的变动 $\mathrm{d} y$ 为:
$$
\begin{aligned}
\mathrm{d} y & =\mathrm{d} x \cdot x^2+\mathrm{d} x \cdot x^2+\mathrm{d} x \cdot x^2 \\
& =3 x^2 \mathrm{~d} x
\end{aligned}
$$

体积的变动率 $\frac{\mathrm{d} y}{\mathrm{~d} x}$ 为:
$$
\frac{\mathrm{d} y}{\mathrm{~d} x}=3 x^2
$$

可以想象, 继续推广到高维空间也是适用的, 这里就不方便做可视化了。

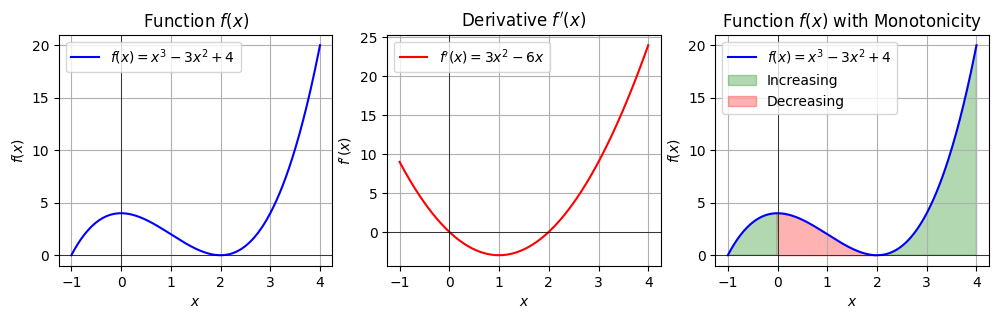
微分与函数的单调性

直接上定义:

$f(x)$ 在 $(a, b)$ 内可导, 如果 $f^{\prime}(x)>0$, 那么函数在 $(a, b)$ 内单调递增;
如果 $f^{\prime}(x)<0$, 那么函数在 $(\mathrm{a}, \mathrm{b})$ 内单调递减。

用微分的定义（微分解释了函数变动的规律）也容易解释单调性, 当$x$的变动引起的函数变动是正增长时，函数单调递增。当$x$的变动引起的函数变动是负增长时，函数单调递减。

import numpy as np
import matplotlib.pyplot as plt

# 定义函数 f(x)
def f(x):
    return x**3 - 3*x**2 + 4

# 定义函数的导数 f'(x)
def df(x):
    return 3*x**2 - 6*x

# 创建 x 轴上的点
x = np.linspace(-1, 4, 400)

# 计算函数值和导数值
y = f(x)
dy = df(x)

# 绘制函数 f(x) 和其导数 f'(x)
plt.figure(figsize=(12, 3))

# 绘制 f(x)
plt.subplot(1, 3, 1)
plt.plot(x, y, label='$f(x) = x^3 - 3x^2 + 4$', color='b')
plt.title('Function $f(x)$')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(True)
plt.legend()

# 绘制 f'(x)
plt.subplot(1, 3, 2)
plt.plot(x, dy, label="$f'(x) = 3x^2 - 6x$", color='r')
plt.title('Derivative $f\'(x)$')
plt.xlabel('$x$')
plt.ylabel("$f'(x)$")
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(True)
plt.legend()

# 绘制 f(x)
plt.subplot(1, 3, 3)
plt.plot(x, y, label='$f(x) = x^3 - 3x^2 + 4$', color='b')
plt.fill_between(x, y, where=(dy > 0), interpolate=True, color='green', alpha=0.3, label='Increasing')
plt.fill_between(x, y, where=(dy < 0), interpolate=True, color='red', alpha=0.3, label='Decreasing')
plt.title('Function $f(x)$ with Monotonicity')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(True)
plt.legend()

plt.show()

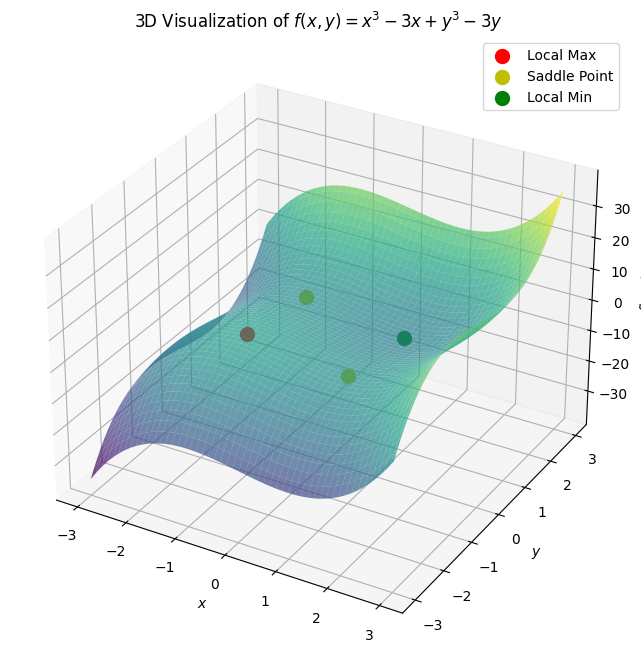
极值与鞍点

极值 (Extrema)：
- 局部最大值 (Local Maximum) : 在某个点 $x=a$ 处，如果函数值 $f(a)$ 大于在其邻域内所有其他点的函数值，则 $f(a)$ 为局部最大值。
- 局部最小值 (Local Minimum) : 在某个点 $x=b$ 处，如果函数值 $f(b)$ 小于在其邻域内所有其他点的函数值，则 $f(b)$ 为局部最小值。
鞍点 (Saddle Point) :
- 鞍点是指在某个点 $x=c$ 处，函数的导数为零，但该点既不是局部最大值也不是局部最小值。

import numpy as np
import matplotlib.pyplot as plt
from sympy import symbols, diff, solve
from mpl_toolkits.mplot3d import Axes3D

# 定义符号变量和函数
x, y = symbols('x y')
f_sym = x**3 - 3*x + y**3 - 3*y
df_sym_x = diff(f_sym, x)
df_sym_y = diff(f_sym, y)

# 求解一阶导数为零的点（临界点）
critical_points = solve((df_sym_x, df_sym_y), (x, y))

# 计算二阶导数并评估临界点的性质
d2f_sym_xx = diff(df_sym_x, x)
d2f_sym_yy = diff(df_sym_y, y)
d2f_sym_xy = diff(df_sym_x, y)

# 可视化
x_vals = np.linspace(-3, 3, 100)
y_vals = np.linspace(-3, 3, 100)
x_vals, y_vals = np.meshgrid(x_vals, y_vals)
f_vals = x_vals**3 - 3*x_vals + y_vals**3 - 3*y_vals

fig = plt.figure(figsize=(14, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制函数 f(x, y)
ax.plot_surface(x_vals, y_vals, f_vals, cmap='viridis', alpha=0.7)

# 标记临界点及其性质
for point in critical_points:
    x_val, y_val = float(point[0]), float(point[1])
    z_val = x_val**3 - 3*x_val + y_val**3 - 3*y_val
    d2f_xx_val = d2f_sym_xx.subs({x: x_val, y: y_val})
    d2f_yy_val = d2f_sym_yy.subs({x: x_val, y: y_val})

    if d2f_xx_val > 0 and d2f_yy_val > 0:
        ax.scatter(x_val, y_val, z_val, color='g', s=100, label='Local Min' if 'Local Min' not in ax.get_legend_handles_labels()[1] else "")
    elif d2f_xx_val < 0 and d2f_yy_val < 0:
        ax.scatter(x_val, y_val, z_val, color='r', s=100, label='Local Max' if 'Local Max' not in ax.get_legend_handles_labels()[1] else "")
    else:
        ax.scatter(x_val, y_val, z_val, color='y', s=100, label='Saddle Point' if 'Saddle Point' not in ax.get_legend_handles_labels()[1] else "")

ax.set_title('3D Visualization of $f(x, y) = x^3 - 3x + y^3 - 3y$')
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_zlabel('$f(x, y)$')
ax.legend()
plt.show()

Hessian Matrix

Hessian矩阵是用来描述一个多元函数在某一点的局部二阶变化情况的方阵。对于一个 $n$ 维函数 $f(\mathbf{x})$ ，其中 $\mathbf{x}=\left(x_1, x_2, \ldots, x_n\right)$ ，赫西矩阵 $H$ 定义为:
$$
H(\mathbf{x})=\left(\begin{array}{cccc}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\
\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2}
\end{array}\right)
$$

其中， $\frac{\partial^2 f}{\partial x_i \partial x_j}$ 表示 $f$ 对 $x_i$ 和 $x_j$ 的二阶偏导数。

Hessian 矩阵主要用于分析多元函数在临界点的性质，即判断这些点是局部极值（最大值或最小值）还是鞍点。具体步骤如下:

找到临界点: 求解一阶偏导数为零的点。
$$
\nabla f(\mathbf{x})=\left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_n}\right)=0
$$
计算Hessian矩阵：在每个临界点处计算赫西矩阵 $H$ 的值。
判别法:
- 计算行列式 $D$ : 计算Hessian矩阵的行列式和特征值来判断临界点的性质。
- 对于二元函数 $f(x, y)$ ，行列式 $D$ 计算如下:
  $$
  D=\operatorname{det}(H)=f_{x x} f_{y y}-\left(f_{x y}\right)^2
  $$

判断临界点的性质:
如果D>0，则是极值。
如果D<0，则是鞍点。
如果D=0，需要进一步分析（通常不能确定性质）。

行列式 D 只是一个工具，用来辅助判断极值与鞍点，如果要准确判断临界点的性质（极大值，极小值），需要通过特征值来帮忙。具体判断方法为：

如果所有特征值均为正，则函数在该点有局部最小值。
如果所有特征值均为负，则函数在该点有局部最大值。
如果特征值有正有负，则函数在该点有鞍点。
如果特征值中有零，需要进一步分析（通常不能确定性质）。

举例函数 $f(x, y)=x^3-3 x+y^3-3 y$ 的分析过程如下:

首先，找到临界点:
$$
\begin{aligned}
& f_x=3 x^2-3=0 \Longrightarrow x= \pm 1 \\
& f_y=3 y^2-3=0 \Longrightarrow y= \pm 1
\end{aligned}
$$
然后，计算Hessian矩阵:

$$
H=\left(\begin{array}{cc}
6 x & 0 \\
0 & 6 y
\end{array}\right)
$$

特征方程为:
$$
\operatorname{det}\left(\begin{array}{cc}
6 x-\lambda & 0 \\
0 & 6 y-\lambda
\end{array}\right)=0
$$

解得特征值 $\lambda_1=6 x$ 和 $\lambda_2=6 y$ 。

在临界点 $(1,1)$ 处:

特征值 $\lambda_1=6 \cdot 1=6>0$
特征值 $\lambda_2=6 \cdot 1=6>0$

因此， $(1,1)$ 是局部最小值。

在临界点 $(1,-1)$ 处:

特征值 $\lambda_1=6 \cdot 1=6>0$
特征值 $\lambda_2=6 \cdot(-1)=-6<0$

因此， $(1,-1)$ 是鞍点。以此类推，可以分析其他临界点的性质。

函数的凹凸性

函数的凹凸性是描述函数形态的一种性质。具体而言，函数的凹凸性可以告诉我们函数曲线是向上弯曲还是向下弯曲的。
凸函数（Convex Function）：几何上，这意味着连接曲线上任意两点的线段都位于曲线之上或重合。
凹函数（Concave Function）：几何上，这意味着连接曲线上任意两点的线段都位于曲线之下或重合。

Hessian矩阵可以用来判断函数的凹凸性。

如果所有特征值均为正，则赫西矩阵是正定的，函数在该点附近是凸的。
如果所有特征值均为负，则赫西矩阵是负定的，函数在该点附近是凹的。
如果特征值有正有负，则函数在该点附近既不是凸的也不是凹的。

链式法则（The Chain Rule）

在机器学习中，尤其是在深度学习和神经网络中，链式法则用于计算复合函数的导数，这在反向传播算法中尤为关键。具体来说，当训练一个深度神经网络时，需要计算损失函数相对于每个权重的梯度。由于神经网络的每一层都是复合的，链式法则能够从输出层逐步回到输入层，计算这些梯度。
先来看一下微分链式法则的数学公式：

$$
\begin{gathered}
y=f(g(x)) \\
\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\mathrm{d} f}{\mathrm{~d} x}=\frac{\mathrm{d} f}{\mathrm{~d} g} \cdot \frac{\mathrm{d} g}{\mathrm{~d} x}=f^{\prime}(g(x)) \cdot \mathrm{g}^{\prime}(x)
\end{gathered}
$$

理解起来很简单，就像剥洋葱一样，一层一层拨开里面的心。链式法则一般用于复合函数的求导，先对外层函数求导，再乘上内层函数的导数。之前一直强调导数是函数的变动规律，那么链式法则就是变动的传导法则。

举例：
$$
\begin{aligned}
& y=\sin \left(x^2\right) \\
& h=x^2 \\
& y=\sin (h)
\end{aligned}
$$

对 $y$ 求导的步骤如下:
$$
\begin{aligned}
& \frac{\mathrm{d} y}{\mathrm{~d} h}=\cos h \quad \mathrm{~d} y=\cos h \mathrm{~d} h \\
& \mathrm{~d} h=\mathrm{d} x^2=2 x \mathrm{~d} x \\
& \mathrm{~d} y=\cos x^2 \cdot 2 x \mathrm{~d} x \Rightarrow \frac{\mathrm{d} y}{\mathrm{~d} x}=\cos x^2 \cdot 2 x
\end{aligned}
$$

解释一下, $x$ 的变动会引起 $h$ 的变动, 进而引起 $y$ 的变动。链式法则就是变动的传导法则。

梯度

梯度的数学定义

对于一个多变量标量函数 $f\left(x_1, x_2, \ldots, x_n\right)$ ，梯度是一个由偏导数组成的向量。梯度向量表示函数 $f$ 在每个方向上的变化率。数学上，梯度可以表示为:
$$
\nabla f=\left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_n}\right)
$$

其中 $\frac{\partial f}{\partial x_i}$ 表示 $f$ 对第 $i$ 个变量 $x_i$ 的偏导数。

梯度的几何解释

梯度向量指向函数值增加最快的方向，其大小等于该方向上的最大变化率。例如，在二维平面上，如果我们有一个标量函数 $f(x, y)$ ，其梯度是:
$$
\nabla f=\left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)
$$

此时，梯度向量 $\nabla f$ 指向 $f$ 值增加最快的方向，并且其长度表示 $f$ 在该方向上的最大变化率。

梯度在深度学习的应用

梯度下降法（Gradient Descent）是一种常用的最优化算法，通过沿梯度的反方向移动，逐步逼近函数的最小值。梯度下降法在机器学习中的参数优化中广泛应用。

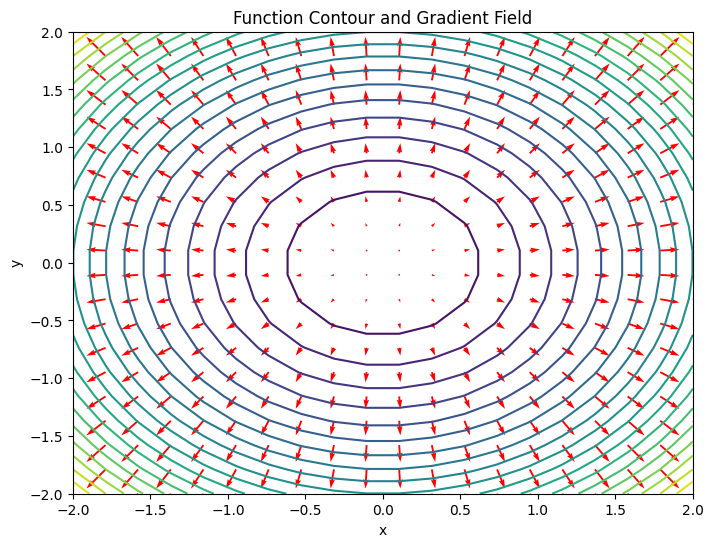
梯度的计算示例
考虑一个简单的二维函数 $f(x, y)=x^2+y^2$ ，我们可以计算其梯度:
$$
\nabla f=\left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)=(2 x, 2 y)
$$

这表明，在任意点 $(x, y)$ ，梯度向量 $(2 x, 2 y)$ 指向函数值增加最快的方向，并且其大小是 $\sqrt{(2 x)^2+(2 y)^2}=2 \sqrt{x^2+y^2}$ 。下面让我们通过绘制一个函数的等高线图（等值线图）以及其梯度场来进一步理解梯度的概念。

import numpy as np
import matplotlib.pyplot as plt

# 定义函数
def f(x, y):
    return x**2 + y**2

# 定义梯度函数
def gradient_f(x, y):
    return np.array([2*x, 2*y])

# 创建网格
x = np.linspace(-2, 2, 20)
y = np.linspace(-2, 2, 20)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)

# 计算梯度
U, V = gradient_f(X, Y)

# 绘制等高线图和梯度场
plt.figure(figsize=(8, 6))
plt.contour(X, Y, Z, levels=20)
plt.quiver(X, Y, U, V, color='r')

plt.title('Function Contour and Gradient Field')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

泰勒公式

泰勒公式允许用多项式来近似复杂的函数，这在算法中有时用于简化计算。例如，在高斯过程回归和一些其他贝叶斯方法中，泰勒展开用于线性化关于后验的计算。
泰勒公式的本质是用简单的多项式来近似拟合复杂的函数。

先回忆一下微分:
$$
\frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x} \approx f^{\prime}\left(x_0\right)
$$

若 $f^{\prime}\left(x_0\right)$ 存在, 在 $x_0$ 附近有 $f\left(x_0+\Delta x\right)-f\left(x_0\right) \approx f^{\prime}\left(x_0\right) \Delta x$, 令 $\Delta x=x-x_0$, 将 $\Delta x$ 带入上式整理得到:
$$
f(x) \approx f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(x-x_0\right)
$$

这就是泰勒公式思想的起源, 即函数 $f(x)$ 可能是一个很复杂的函数, 甚至复杂到写不出函数公式, 但可以用该函数中某点 $\mathrm{P}$ 的函数值 $f\left(x_0\right)$ 和导数 $f^{\prime}\left(x_0\right)$ 进行近似, 进一步解释一下, 首先希望近似函数能通过给定的点, 比如点 $\mathrm{P}$ 的函数值 $f\left(x_0\right)$, 然后, 为了确保近似函数的形状与原函数相似, 我们希望它们在点 $\mathrm{P}$ 的斜率是一样的, 这就是求一阶导数的原因。

但是，仅仅知道在点P的斜率可能不足以描述整个函数的形状。为了更好地模拟函数的形状，可能需要考虑函数的弯曲程度，也就是凹凸性。这就是为什么要考虑二阶导数。然后，为了捕捉更多的细节，可能还需要三阶、四阶甚至更高阶的导数，导数阶数越多对函数的约束能力越强，越能拟合出一个确定的函数。所以泰勒公式可以写成：

$$
P_n(x)=f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(x-x_0\right)+\frac{f^{\prime \prime}\left(x_0\right)}{2!}\left(x-x_0\right)^2+\cdots+\frac{f^{(n)}\left(x_0\right)}{n!}\left(x-x_0\right)^n
$$

刚刚介绍了导数阶数, 下面想想 $\left(x-x_0\right)^n, n=1,2,3 \cdots$ 这个多项式有什么用?

分别求 $f(x)=e^x$ 在点 $x=0$ 处的各阶多项式, 如下代码：

import numpy as np
import matplotlib.pyplot as plt

# 定义原函数和泰勒展开的各项
def f(x):
    return np.exp(x)

def taylor_approx(x, n):
    result = 0
    for i in range(n + 1):
        result += (x**i) / np.math.factorial(i)
    return result

# 生成数据点
x = np.linspace(-2, 2, 400)
y = f(x)

# 创建图像和2x2的子图
fig, axs = plt.subplots(2, 2, figsize=(6, 6))

# 绘制不同阶数的泰勒多项式近似
for n, ax in zip(range(1, 5), axs.ravel()):
    ax.plot(x, y, label='$e^x$', color='black')
    ax.plot(x, taylor_approx(x, n), label=f'Taylor Polynomial (n={n})')
    ax.set_title(f'Taylor Series Approximation of $e^x$ at $x=0$, n={n}')
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.legend()
    ax.grid(True)

# 调整布局以防止标签重叠
plt.tight_layout()
plt.show()

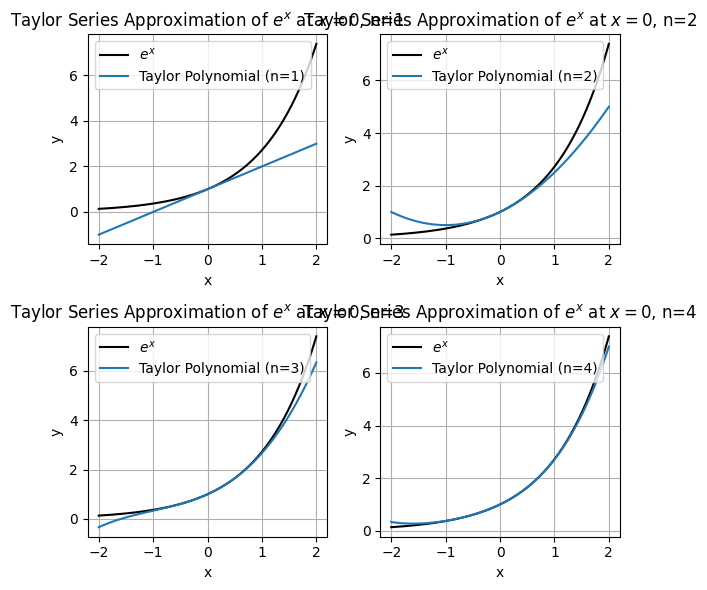
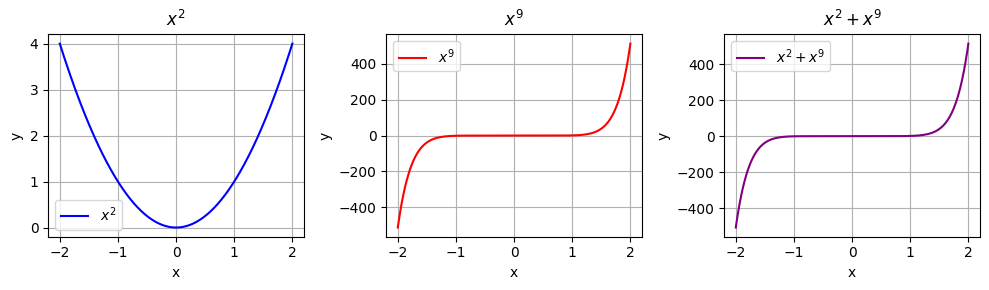
想象用一条曲线来近似描述一座山的形状（复杂函数）。如果只使用直线（线性函数），可能只能大致描述山的一个斜坡。但如果使用了一个曲线（比如二次函数或更高次的函数），就可以更准确地描述山的轮廓。也就是说低阶项（如线性或二次项）通常在函数的起始部分起主导作用，而高阶项（如三次、四次或更高的项）在函数的远端起主导作用。这就是为什么泰勒公式中有多项式的原因。最后解释一下阶乘 $n!$ 的作用, 如下所示, 分别表示 $x^2$ 和 $x^9$ 。当 $x$ 取值较大时, $x^2$ 完全被 $x^9$ 压制, $x^9+x^2$ 几乎只有 $x^9$ 的特性。因此由于高阶的幂函数增长太快,需要除阶乘来减缓增速。

import numpy as np
import matplotlib.pyplot as plt

# 生成数据点
x = np.linspace(-2, 2, 400)

# 定义幂函数
y_x2 = x**2
y_x9 = x**9
y_sum = x**2 + x**9

# 创建图像和3x1的子图
fig, axs = plt.subplots(1, 3, figsize=(10, 3))

# 绘制 $x^2$ 图像
axs[0].plot(x, y_x2, label='$x^2$', color='blue')
axs[0].set_title('$x^2$')
axs[0].set_xlabel('x')
axs[0].set_ylabel('y')
axs[0].legend()
axs[0].grid(True)

# 绘制 $x^9$ 图像
axs[1].plot(x, y_x9, label='$x^9$', color='red')
axs[1].set_title('$x^9$')
axs[1].set_xlabel('x')
axs[1].set_ylabel('y')
axs[1].legend()
axs[1].grid(True)

# 绘制 $x^2 + x^9$ 图像
axs[2].plot(x, y_sum, label='$x^2 + x^9$', color='purple')
axs[2].set_title('$x^2 + x^9$')
axs[2].set_xlabel('x')
axs[2].set_ylabel('y')
axs[2].legend()
axs[2].grid(True)

# 调整布局以防止标签重叠
plt.tight_layout()
plt.show()

最后，再提一下泰勒公式的本质：当一个复杂函数太复杂不可求时，可以用该函数某点的值和该点的多阶导数进行拟合。

Fourier series

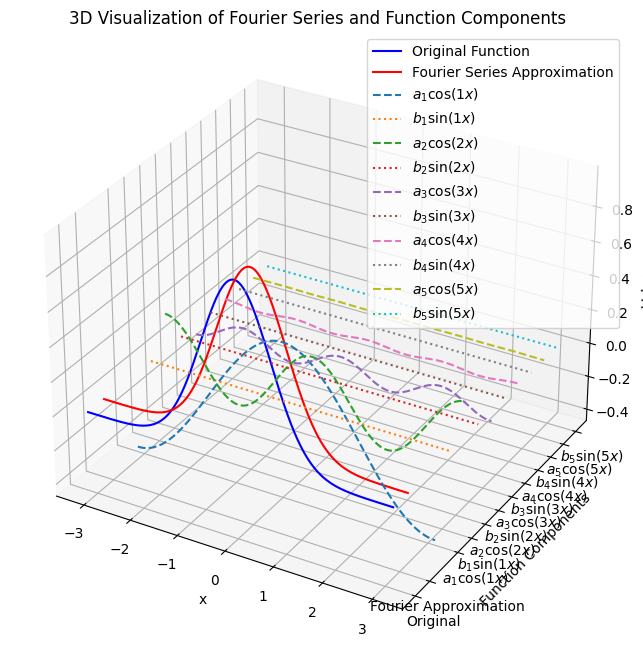
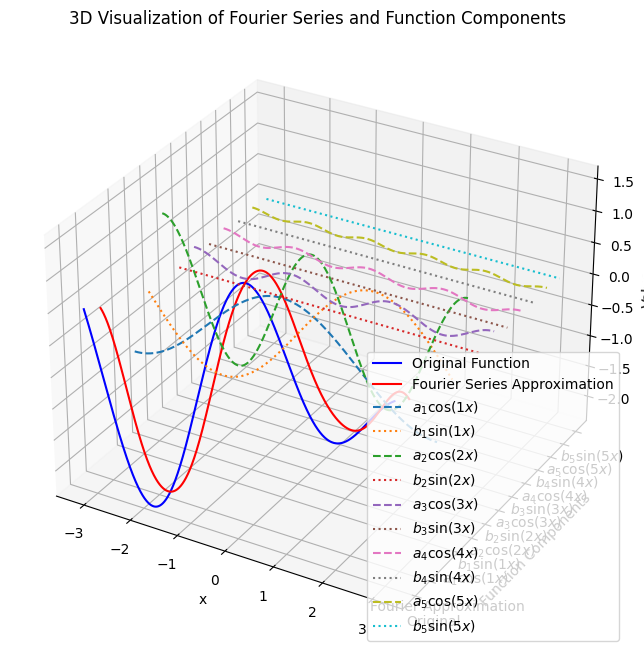
傅里叶级数是一种用三角函数（正弦和余弦函数）的无穷级数来表示周期函数的方法。这个方法由法国数学家约瑟夫·傅里叶提出，并在许多数学和工程领域得到了广泛应用。
傅里叶级数的基本思想是将一个周期函数分解为不同频率的正弦和余弦函数的和。

对于一个周期为 $2 \pi$ 的函数 $f(x)$ ，它可以表示为:
$$
f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left(a_n \cos (n x)+b_n \sin (n x)\right)
$$

其中:

$a_0$ 是函数的平均值（直流分量），由以下公式计算:

$$
a_0=\frac{1}{\pi} \int_{-\pi}^\pi f(x) d x
$$

$a_n$ 和 $b_n$ 是傅里叶系数，分别表示余弦项和正弦项的系数，计算公式为:

$$
\begin{aligned}
& a_n=\frac{1}{\pi} \int_{-\pi}^\pi f(x) \cos (n x) d x \\
& b_n=\frac{1}{\pi} \int_{-\pi}^\pi f(x) \sin (n x) d x
\end{aligned}
$$

这些系数 $a_n$ 和 $b_n$ 描述了函数在不同频率的正弦和余弦成分的幅度。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Define the function f(x)
def f(x):
    return np.sin(x) + 0.5 * np.cos(2 * x) +np.cos(1.5 * x) # Example function, you can change this to any 2π periodic function

# Number of terms in the Fourier series
N = 5

# Calculate Fourier coefficients
a0 = (1 / np.pi) * np.trapz(f(np.linspace(-np.pi, np.pi, 1000)), np.linspace(-np.pi, np.pi, 1000))
an = [(1 / np.pi) * np.trapz(f(np.linspace(-np.pi, np.pi, 1000)) * np.cos(n * np.linspace(-np.pi, np.pi, 1000)), np.linspace(-np.pi, np.pi, 1000)) for n in range(1, N+1)]
bn = [(1 / np.pi) * np.trapz(f(np.linspace(-np.pi, np.pi, 1000)) * np.sin(n * np.linspace(-np.pi, np.pi, 1000)), np.linspace(-np.pi, np.pi, 1000)) for n in range(1, N+1)]

# Create the Fourier series approximation
def fourier_series(x, a0, an, bn, N):
    result = a0 / 2
    for n in range(1, N+1):
        result += an[n-1] * np.cos(n * x) + bn[n-1] * np.sin(n * x)
    return result

# Prepare the data
x = np.linspace(-np.pi, np.pi, 1000)
y_original = f(x)
y_approx = fourier_series(x, a0, an, bn, N)

# Create a figure for 3D plotting
fig = plt.figure(figsize=(14, 8))
ax = fig.add_subplot(111, projection='3d')

# Plot the original function
ax.plot(x, y_original, zs=0, zdir='y', label='Original Function', color='b')

# Plot the Fourier series approximation
ax.plot(x, y_approx, zs=1, zdir='y', label='Fourier Series Approximation', color='r')

# Plot individual sine and cosine components
for n in range(1, N+1):
    ax.plot(x, an[n-1] * np.cos(n * x), zs=2 + 2 * n - 1, zdir='y', label=f'$a_{n} \cos({n}x)$', linestyle='dashed')
    ax.plot(x, bn[n-1] * np.sin(n * x), zs=2 + 2 * n, zdir='y', label=f'$b_{n} \sin({n}x)$', linestyle='dotted')

# Set labels and title
ax.set_xlabel('x')
ax.set_ylabel('Function Components')
ax.set_zlabel('Value')
ax.set_title('3D Visualization of Fourier Series and Function Components')

# Set yticks to show labels clearly
yticks = [0, 1] + [2 + 2 * n - 1 for n in range(1, N+1)] + [2 + 2 * n for n in range(1, N+1)]
ytick_labels = ['Original', 'Fourier Approximation'] + [f'$a_{n} \cos({n}x)$' for n in range(1, N+1)] + [f'$b_{n} \sin({n}x)$' for n in range(1, N+1)]
ax.set_yticks(yticks)
ax.set_yticklabels(ytick_labels)

ax.legend()
plt.show()

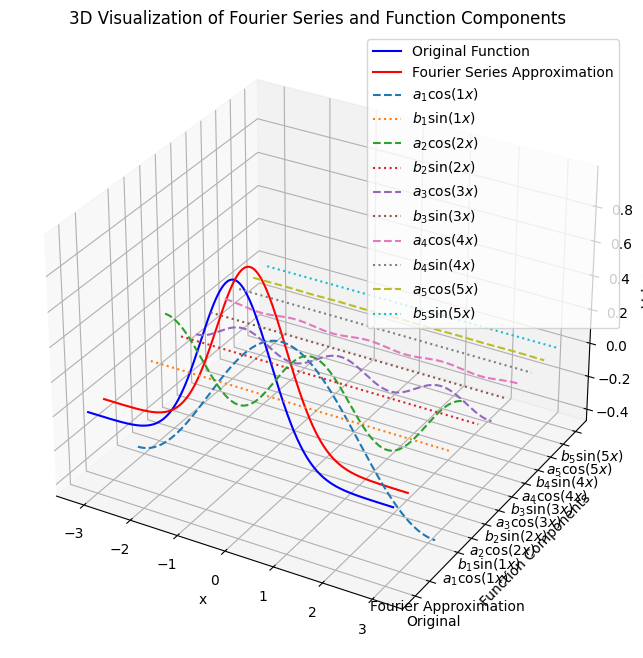
对于非周期函数，通常的做法是：

截断函数：将非周期函数在某个有限区间内进行截断，使其在该区间内近似周期。对于截断后的函数，可以使用傅里叶级数在该有限区间内进行近似。
傅里叶变换：通过傅里叶变换分析函数的频谱，找到其在频域中的表示。傅里叶变换可以将任何函数表示为正弦和余弦函数的线性组合。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Define the function f(x)
def f(x):
    return np.exp(-x**2)  # Example non-periodic function, Gaussian

# Number of terms in the Fourier series
N = 5

# Calculate Fourier coefficients
a0 = (1 / np.pi) * np.trapz(f(np.linspace(-np.pi, np.pi, 1000)), np.linspace(-np.pi, np.pi, 1000))
an = [(1 / np.pi) * np.trapz(f(np.linspace(-np.pi, np.pi, 1000)) * np.cos(n * np.linspace(-np.pi, np.pi, 1000)), np.linspace(-np.pi, np.pi, 1000)) for n in range(1, N+1)]
bn = [(1 / np.pi) * np.trapz(f(np.linspace(-np.pi, np.pi, 1000)) * np.sin(n * np.linspace(-np.pi, np.pi, 1000)), np.linspace(-np.pi, np.pi, 1000)) for n in range(1, N+1)]

# Create the Fourier series approximation
def fourier_series(x, a0, an, bn, N):
    result = a0 / 2
    for n in range(1, N+1):
        result += an[n-1] * np.cos(n * x) + bn[n-1] * np.sin(n * x)
    return result

# Prepare the data
x = np.linspace(-np.pi, np.pi, 1000)
y_original = f(x)
y_approx = fourier_series(x, a0, an, bn, N)

# Create a figure for 3D plotting
fig = plt.figure(figsize=(14, 8))
ax = fig.add_subplot(111, projection='3d')

# Plot the original function
ax.plot(x, y_original, zs=0, zdir='y', label='Original Function', color='b')

# Plot the Fourier series approximation
ax.plot(x, y_approx, zs=1, zdir='y', label='Fourier Series Approximation', color='r')

# Plot individual sine and cosine components
for n in range(1, N+1):
    ax.plot(x, an[n-1] * np.cos(n * x), zs=2 + 2 * n - 1, zdir='y', label=f'$a_{n} \cos({n}x)$', linestyle='dashed')
    ax.plot(x, bn[n-1] * np.sin(n * x), zs=2 + 2 * n, zdir='y', label=f'$b_{n} \sin({n}x)$', linestyle='dotted')

# Set labels and title
ax.set_xlabel('x')
ax.set_ylabel('Function Components')
ax.set_zlabel('Value')
ax.set_title('3D Visualization of Fourier Series and Function Components')

# Set yticks to show labels clearly
yticks = [0, 1] + [2 + 2 * n - 1 for n in range(1, N+1)] + [2 + 2 * n for n in range(1, N+1)]
ytick_labels = ['Original', 'Fourier Approximation'] + [f'$a_{n} \cos({n}x)$' for n in range(1, N+1)] + [f'$b_{n} \sin({n}x)$' for n in range(1, N+1)]
ax.set_yticks(yticks)
ax.set_yticklabels(ytick_labels)

ax.legend()
plt.show()

Credits

Icons made by Becris from www.flaticon.com
Icons from Icons8.com - https://icons8.com
Datasets from Kaggle - https://www.kaggle.com/
Introduction to AutoDiff by Alexey Radul
Gentle Introduction to AutoDiff by Boris Ettinger
Statistical Machine Learning - Automatic Differentiation and Neural Networks - Jason Domke
AUTOGRAD: AUTOMATIC DIFFERENTIATION
Tal Daniel

Deep Learning Math

高等数学（Advanced Mathematics）

Agenda

微积分

积分（integration）

微分和导数

导数的精细的除法

导数的解读

微分与函数的单调性

极值与鞍点

Hessian Matrix

函数的凹凸性

链式法则（The Chain Rule）

梯度

泰勒公式

Fourier series

Credits

发表回复取消回复

作者

Tutorial 01 – 师徒相授：有监督学习（Supervised Learning）

SE(3)-Transformers

ComENet

强化学习（DRL）

Deep Learning Math

高等数学（Advanced Mathematics）

Agenda

微积分

积分（integration）

微分和导数

导数的精细的除法

导数的解读

微分与函数的单调性

极值与鞍点

Hessian Matrix

函数的凹凸性

链式法则（The Chain Rule）

梯度

泰勒公式

Fourier series

Credits

发表回复 取消回复

作者

相关文章

发表回复取消回复