Deep Learning Math

群论（group Theory）

在学习几何深度学习之前，具备群论的基础知识是非常重要的，原因在于几何深度学习处理的数据和问题往往涉及到复杂的空间变换和对称性，例如，分子结构在旋转或镜像反射后可能保持不变，三维物体的形状在不同视角下具有旋转对称性。识别和利用这些对称性对于理解数据的本质特征至关重要。而群论恰恰提供了一种强大的数学工具来描述和理解这些变换和对称性。通过使用群论的概念设计的深度学习模型能够更好地理解和利用数据的内在对称性，从而提高模型在未见数据上的泛化能力。对于变换不变性和等变性的理解有助于构建在面对数据变换时依然稳定表现的模型，这对于许多实际应用至关重要。

Agenda

群的定义(Definition of Group)
对称性(Symmetry)
不变性(Invariance)
等变性(Equivariance)
S0(3) Group
群的表示(Representation of Groups)

群的定义(Definition of Group)

群是数学中的一个基本概念，它提供了一种描述对称性、操作及其性质的形式化方法。群的严格数学定义如下：

一个群是一个集合 $G$, 配合一个二元运算, 满足以下四个条件:

封闭性(Closure): 对于集合 $G$ 中任意两个元素 $a$ 和 $b$, 运算的结果 $a \cdot b$ 也在 $G$ 中。即,集合对于这个运算是封闭的。
结合律(Associativity): 对于集合 $G$ 中任意三个元素 $a 、 b$ 和 $c$, 运算满足结合律 $(a \cdot b) \cdot c=a \cdot(b \cdot c) 。$
单位元素(Identity Element): 在集合 $G$ 中存在一个特殊的元素 $e$, 对于集合中的任意元素 $a$, 它与 $e$ 的运算结果仍然是 $a: a \cdot e=e \cdot a=a$ 。这个元素 $e$ 被称为单位元素或恒等元素。
逆元素(Inverse Element): 对于集合 $G$ 中的每个元素 $a$, 存在另一个元素 $b$ 在 $G$ 中, 使得 $a$ 和 $b$ 的运算结果是单位元素 $e: a \cdot b=b \cdot a=e$ 。这个元素 $b$ 被称为元素 $a$ 的逆元素。

简单说，群就是“集合+运算”

考虑一个关于时间的例子来说明群的概念。
想象你有一个非常特别的手表，这个手表有四个按钮，每个按钮代表一个操作：快进1小时（A）；后退1小时（B）；时间不变（C）。
在这个设置中，集合为{A,B,C}，操作为按下按钮。
封闭性的体现为：无论你按哪两个按钮，或者是同一个按钮多次，得到的时间变化都可以通过再按其他按钮中的某一个来达到。例如，按下快进1小时（A）和后退1小时（B）的组合，等同于时间不变（C）。这意味着所有可能的时间变化操作都包含在这个按钮集合内。
结合律体现在按钮操作的组合顺序不会影响最终的时间变化结果。例如，无论是先组合A和B再应用C，还是先将B与C组合再与A组合，最终结果始终保持时间不变（C）。
时间不变按钮（G）就是这个手表操作集合的单位元素。按下这个按钮不会改变当前的时间，它确保了无论你之前进行了什么操作，再按下时间不变按钮都不会改变当前的时间状态。
对于这个手表上的每个按钮，都有一个对应的逆操作按钮。比如，快进1小时（A）的逆操作是后退1小时（B）。按下一个按钮然后按下它的逆操作按钮，会使时间状态回到按下第一个按钮之前的状态。

对称性(Symmetry)

群论在描述对称性方面扮演着核心角色，提供了一套严格的数学框架，用以分析和理解对称性的本质。对称性是指某个对象或系统在经过一系列变换（如旋转、反射、平移等）后，仍能保持其某些特征或性质不变的属性。这些变换构成了一个群，称为对称群，它准确描述了系统的对称操作。

在数学、物理、化学、生物学等众多科学领域内，对称性不仅是一种常见的现象，也是理解系统性质的关键因素。

通过群论，我们能够将对称性的概念数学化，进而揭示系统的内在规律和性质。

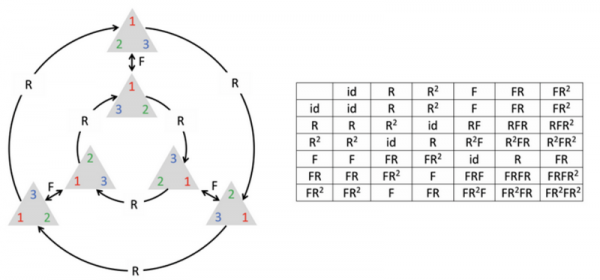
例如，我们考虑数学中的等边三角形的对称群D3，有时也称为S3，它表示三角形所有可能的旋转和反射操作。这个对称群可以完全由两个操作来生成：旋转R和反射F，如图

旋转（R）：图1-37中的R代表着围绕三角形中心顺时针旋转60度。旋转两次（R2）意味着旋转了120度，而旋转三次相当于旋转了180度，这实际上会使三角形回到原来的位置（在群的语境中相当于做了一个恒等操作，或者说没有改变，用id表示）。
反射（F）：例如，F代表着沿一条通过顶点1和三角形中心的线进行反射。这种反射会改变顶点2和3的位置。同理，在顶点2和3也可以沿中心线进行反射。

等边三角形的对称群包含6个元素：恒等操作id，两个旋转（R和R2），以及三个反射（F, FR和FR2）。这些元素组成了群D3的所有可能操作。

图的右边是一个乘法表（或称作群的运算表），展示了每对操作组合的结果。例如，FR在表中的意思是先进行反射F再进行旋转R。每一行代表一个操作，每一列也代表一个操作，交点则代表这两个操作的组合结果。例如，在R行和F列的交点是RF，这表明如果我们先旋转再反射，最终的效果等同于单一操作RF。

这个群的结构揭示了等边三角形的所有可能对称性。通过研究这个群，我们可以了解三角形在不同操作下的行为，以及这些操作如何相互关联。该群的每个元素都是等价的，意味着群中的每个元素都可以通过其他元素的组合来表达。此外，这个群是非阿贝尔群（非交换群），因为某些操作的组合结果取决于它们的顺序（例如，RF不同于FR）。

不变性与等变性(Invariance and Equivariance)

此外，在深度学习中，对称性一般被细分为不变性与等变性。

不变性意味着模型输出对于某种操作或变换是不变的。
等变性是指当输入数据经历某种变换时，模型输出也会以相同的方式变换。

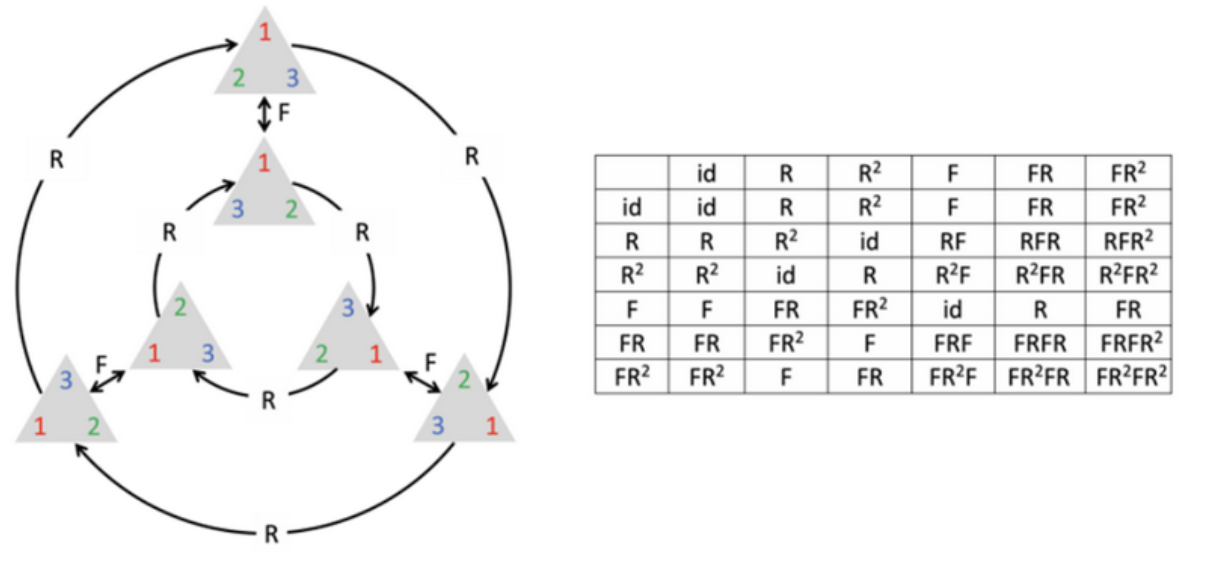
延续上图中等变三角形的例子。当绕三角形中心旋转120°，240°或360°时，三角形的外观和位置看起来完全一样，这体现了其对称性。

当三角形绕中心旋转120°或240°时，尽管最终的形状看起来与原始形状相同，但三角形的每个顶点实际上已经移动到了新的位置。这种顶点位置的改变是等变性的体现：输入（三角形的旋转）导致了输出（顶点位置）的对应变化。
当旋转360°，即完全旋转一周后，三角形的每个顶点都恢复到了其原始位置。从整体上看，三角形看起来没有任何变化，即三角形的整体形状和位置与原始状态相同。这是不变性的体现：尽管进行了操作（旋转360°），输出（三角形的整体形状和位置）保持不变。

SO(3) Group

SO(3)群是所有 $3 \times 3$ 的正交矩阵组成的群

这些矩阵的行列式为 1 。正交矩阵具有性质 $R R^T=I$ ，其中 $R^T$ 是矩阵 $R$ 的转置， $I$ 是单位矩阵。
正交矩阵保证了旋转不会改变向量的长度。
行列式为1则保证了旋转操作是不改变物体体积的，即没有反射或缩放发生。
这些矩阵代表了三维空间下的所有旋转操作，它包括了所有可能的角度和绕任意轴的旋转，这意味着它能够描述或模拟现实世界中任何物体的旋转动作。
值得注意的是，这些旋转操作保持向量的长度和夹角，以及整体的空间体积，但并不保证旋转后的对象会保持原有的对称性或外观。

SO(3)群的性质包括:

闭合性: 两个 SO(3)群的元素 (旋转) 的组合 (即矩阵乘法) 仍然是SO(3)群的元素。
单位元存在性: 单位矩阵 $I$ 是 $\mathrm{SO}(3)$ 群的单位元，表示无旋转。
逆元存在性: 每个旋转矩阵 $R$ 在 $\mathrm{SO}(3)$ 群中都有一个逆元 $R^{-1}=R^T$ ，也是一个旋转，使得 $R R^T=I$ 。
结合性: 对于任意三个元素 $R_1, R_2, R_3$, 满足 $\left(R_1 R_2\right) R_3=R_1\left(R_2 R_3\right)$ 。

总的来说，SO3群提供了一种精确的数学工具，用于模拟和理解真实世界中的旋转现象，这些旋转现象在我们的日常生活和高科技行业中无处不在。

群的表示(Representation of Groups)

群的表示（Group Representation）提供了一种方式来“实现”群的抽象概念，将群的元素表现为矩阵或线性算子，这使得群的结构和群作用可以通过矩阵的运算和性质来分析和理解。

以SO(3)群为例，群表示空间是三维空间，因为SO(3)自然地作用于三维空间。

在这个空间中，每个SO(3)群的元素可以通过一个3×3的实正交矩阵来表示，这个矩阵在三维空间中执行一个旋转操作，表示旋转的轴和角度。
且矩阵满足两个条件：其转置等于其逆矩阵，且其行列式为1。

下面具体展示在笛卡尔坐标系下, 绕三个主轴一即 $x$ 轴、 $y$ 轴和 $z$ 轴的 $\mathrm{SO}(3)$ 旋转矩阵的群表示, 该表示维数为 3 （三维空间）, 这意味着表示空间是由三个基向量张成的, 任何旋转都可以表示为这三个基向量的线性组合, 它们分别是:

绕 $z$ 轴旋转的矩阵 $R_3(\psi)$, 表示为:
$$
R_3(\psi)=\left(\begin{array}{ccc}
\cos \psi & -\sin \psi & 0 \\
\sin \psi & \cos \psi & 0 \\
0 & 0 & 1
\end{array}\right)
$$

这表示一个对象绕 $z$ 轴逆时针旋转了角度 $\psi$ 的旋转。

绕 $y$ 轴旋转的矩阵 $R_2(\phi)$, 表示为:
$$
R_2(\phi)=\left(\begin{array}{ccc}
\cos \phi & 0 & \sin \phi \\
0 & 1 & 0 \\
-\sin \phi & 0 & \cos \phi
\end{array}\right)
$$

这表示一个对象绕 $y$ 轴逆时针旋转了角度 $\phi$ 的旋转。

绕 $x$ 轴旋转的矩阵 $R_1(\theta)$, 表示为:
$$
R_1(\theta)=\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\
0 & \sin \theta & \cos \theta
\end{array}\right)
$$

这表示一个对象绕 $x$ 轴逆时针旋转了角度 $\theta$ 的旋转。

这些矩阵是SO(3)群的标准基础元素，也是构建更复杂旋转的基本构件。

在实际应用中，任意的旋转都可以通过这些基础旋转的组合来实现。

这些矩阵的特点是：
- 它们都是正交的（即矩阵乘以它的转置等于单位矩阵）且行列式为1，正好符合SO(3)群的定义。
- SO(3)群的表示是同态的，这意味着如果我们将SO(3)群的两个元素（两个旋转矩阵）相乘，结果也应该是SO(3)群内的一个元素，并且这个乘法运算在表示空间上是连续的。
- 换句话说，旋转的组合对应于这些旋转矩阵的矩阵乘法。笛卡尔坐标系下SO(3)旋转矩阵的群表示将旋转这一抽象概念具象化，来描述和计算三维空间中对象的取向变化。

另一种描述三维旋转的常见方法是欧拉角, 它可以被看作是一系列按特定顺序执行的旋转的组合。