概率与统计

 Deep Learning Math
Deep Learning Math
概率与统计(Probability and Statistics)
概率论和统计学在深度学习中至关重要。概率论为模型的不确定性和预测提供理论基础。数据位置和数据散布的概念帮助我们理解和描述数据的中心趋势和变异性。图形表示技术,如直方图和散点图,用于数据的可视化和探索。离散型概率分布和连续型概率分布则用于描述不同类型的数据和其分布模式。
在统计学中,点估计和区间估计用于推断数据的参数,从而帮助我们理解模型的预测准确性和置信区间。假设性检验用于评估模型假设的有效性和显著性,确保结果的可靠性。相关性分析则用于发现变量之间的关系和依赖性,从而帮助我们优化模型和提升性能。通过概率论和统计学工具,深度学习能够更好地处理数据的不确定性、进行模型评估和优化,提升预测的准确性和可靠性。
 Agenda
Agenda
-
概率论(Probability Theory)
- 数据位置
- 数据散布
- 图形表示
- 离散型概率分布
- 连续型概率分布
-
统计学(Statistics)
- 点估计
- 蒙特卡洛采样
- 区间估计
- 假设性检验
- 相关性分析
 Additional Packages for Google Colab
Additional Packages for Google Colab
If you are using Google Colab, you have to install additional packages. To do this, simply run the following cell.
 概率论
概率论
 数据位置
数据位置
平均数(Average)是表示一组数据集中趋势的量数,是指在一组数据中所有数据之和再除以这组数据的个数,是反映数据集中趋势的一项指标。
特点:
- (1)易受极端值影响。
- (2)数学性质优良。
- (3)数据对称分布或接近对称分布时应用。
众数(Mode)是指在统计分布上具有明显集中趋势点的数值,代表数据的一般水平。 也是一组数据中出现次数最多的数值,有时众数在一组数中有好几个,用M表示。
特点:
- (1)组数据中出现次数最多的变量值。
- (2)适合于数据量较多时使用。
- (3)不受极端值的影响。
- (4)一组数据可能没有众数也可能有几个众数。
中位数(Median)又称中值,统计学中的专有名词,是按顺序排列的一组数据中居于中间位置的数,代表一个样本、种群或概率分布中的一个数值,其可将数值集合划分为相等的上下两部分。对于有限的数集,可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个,通常取最中间的两个数值的平均数作为中位数。
特点:
- (1)不受极端值的影响。在有极端数值出现时,中位数作为分析现象中集中趋势的数值,比平均数更具有代表性。
- (2)主要用于顺序数据,也可以用于数值型数据,但不能用于分类数据。
- (3)各变量值与中位数的离差绝对值之和最小。
四分位数(Quartile)也称四分位点,是指在统计学中把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值就是四分位数。四分位数多应用于统计学中的箱线图绘制。它是一组数据排序后处于25%和75%位置上的值。四分位数是通过3个点将全部数据等分为4部分,其中每部分包含25%的数据。很显然,中间的四分位数就是中位数,因此通常所说的四分位数是指处在25%位置上的数值(称为下四分位数)和处在75%位置上的数值(称为上四分位数)。与中位数的计算方法类似,根据未分组数据计算四分位数时,首先对数据进行排序,然后确定四分位数所在的位置,该位置上的数值就是四分位数。
假设我们有以下一组数据:
$$
7,15,36,39,40,41,42,43,44,49,50
$$
对于奇数个数据,中位数是第 $\frac{n+1}{2}$ 个数据。
这里数据个数 $n=11$ ,所以中位数位置是第 $\frac{11+1}{2}=6$ 个数据。所以中位数 $Q_2$ 是第 6 个数据,也就是 41 。
下四分位数是位于第 $\frac{n+1}{4}$ 个数据。
这里数据个数 $n=11$ ,所以下四分位数位置是第 $\frac{11+1}{4}=3$ 个数据。
所以下四分位数 $Q_1$ 是第 3 个数据,也就是 36 。
上四分位数是位于第 $\frac{3(n+1)}{4}$ 个数据。
这里数据个数 $n=11$ ,所以上四分位数位置是第 $\frac{3(11+1)}{4}=9$ 个数据。所以上四分位数 $Q_3$ 是第 9 个数据,也就是 44 。
 数据散布
数据散布
数学期望
数学期望(Mathematical expectations)是对长期价值的数字化衡量。
数学期望值是理想状态下得到的实验结果的平均值,是试验中每次可能的结果概率乘以其结果的总和,是最基本的数学特征之一,它反映随机变量平均取值的大小。换句话说,期望值像是随机试验在同样的机会下重复多次,所有那些可能状态的平均结果。
-
离散型随机变量数学期望严格的定义为: 设离散型随机变量 $X$ 的分布列为$P\lbrace X=x_i \rbrace = p_i, \quad i=1,2, \cdots$。若级数 $\sum_{i=1}^{+\infty} x_i p_i$ 绝对收敛, 则称级数 $\sum_{i=1}^{+\infty} x_i p_i$ 的和为随机变量 $X$ 的数学期望(也称期望或均值), 记为 $E(X)$ 。即$E(X)=x_1 p_1+x_2 p_2+\cdots+x_i p_i+\cdots=\sum_{i=1}^{+\infty} x_i p_i$ 。
-
连续型随机变量数学期望严格的定义为: 设连续型随机变量 $X$ 的概率密度函数为 $f(x)$,积分 $\int_{-\infty}^{+\infty} x f(x) d x$ 绝对收敛, 则定义 $x$ 的数学期望 $E(X)$ 为 $E(X)=\int_{-\infty}^{+\infty} x f(x) d x$ 。
一个随机变量的数学期望是一个常数,它表示随机变量取值的一个平均;这里用的不是算术平均,而是以概率为权重的加权平均。数学期望反映了随机变量的一大特征,即随机变量的取值将集中在其期望值附近,这类似于物理中质点组成的质心。
最后,强调一下平均数和数学期望的联系:平均数是一个统计学概念,期望是一个概率论概念。平均数是实验后根据实际结果统计得到的样本的平均值,期望是实验前根据概率分布“预测”的样本的平均值。之所以说“预测”是因为在实验前能得到的期望与实际实验得到的样本的平均数总会不可避免地存在偏差,毕竟随机实验的结果永远充满着不确定性。期望就是平均数随样本趋于无穷的极限。
方差
方差(Variance)用来描述随机变量与数学期望的偏离程度。
如果把单个数据点称为“ $X_i$ ”, 那么 “ $X_1$ ” 是第一个值, “ $X_2$ ” 是第二个值, 以此类推, 一共有 $n$ 个值。均值称为 “ $\mathrm{M}$ ”。
-
初看上去 $\sum\left(X_i-\mathrm{M}\right)$ 就可以作为描述数据点散布情况的指标, 也就是把每个 $X_i$与$M$的偏差求和。换句话讲,是单个数据点减去数据点的平均的总和。
- 此方法看上去很有逻辑性,但却有一个致命的缺点:高出均值的值和低于均值可以相互抵消,因此上述定义的结果趋近于0。
- 这个问题可以通过取差值的绝对值来解决(也就是说,忽略负值的符号),但是由于各种原因,统计学家不喜欢绝对值。另外一个剔除负号的方法是取平方,因为任何数的平方肯定是正的,因此便得到了方差的分子$\sum\left(X_i-\mathrm{M}\right)^2$
-
再考虑一个问题: 比如有 25 个值的样本, 根据方差计算出标准差是 10 。如果把这 25 个值复制一下变成 50 个样本呢, 直觉上 50 个样本的数据点分布情况应该不变的, 但是公式中的累加会产生更大的方差值。
- 所以需要通过除以数据点数量 $n$ 来弥补这个漏洞。
因此, 方差的定义如下:
$$
D(X)=\frac{\sum_{i=1}^N\left(x_i-\bar{x}_i\right)^2}{n}
$$
标准差
标准差(standard deviation)是通过方差除以样本量再开根号得到的,具体公式如下:
$$
\sigma=\sqrt{\frac{\sum_{i=1}^N\left(x_i-\bar{x}_i\right)^2}{n}}
$$
与方差的作用类似, 标准差也能反映一个数据集的离散程度, 它是各点与均值的平均距离。平均数相同的数据, 标准差未必相同。
极差
极差又称范围误差或全距(Range),以R表示,计算方法是其最大值与最小值之间的差距,即最大值减最小值后所得数据。
四分数范围
四分位数,即把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值就是四分位数。第三四分位数与第一四分位数的差值称为四分位数间距(Interquartile Range,IQR),简称四分位距。
四分位距是描述统计学中的一种方法,但由于四分位距不受极大值或极小值的影响,常用于描述非正态分布资料的离散程度,其数值越大,数据离散程度越大,反之离散程度越小。
 图形表示
图形表示
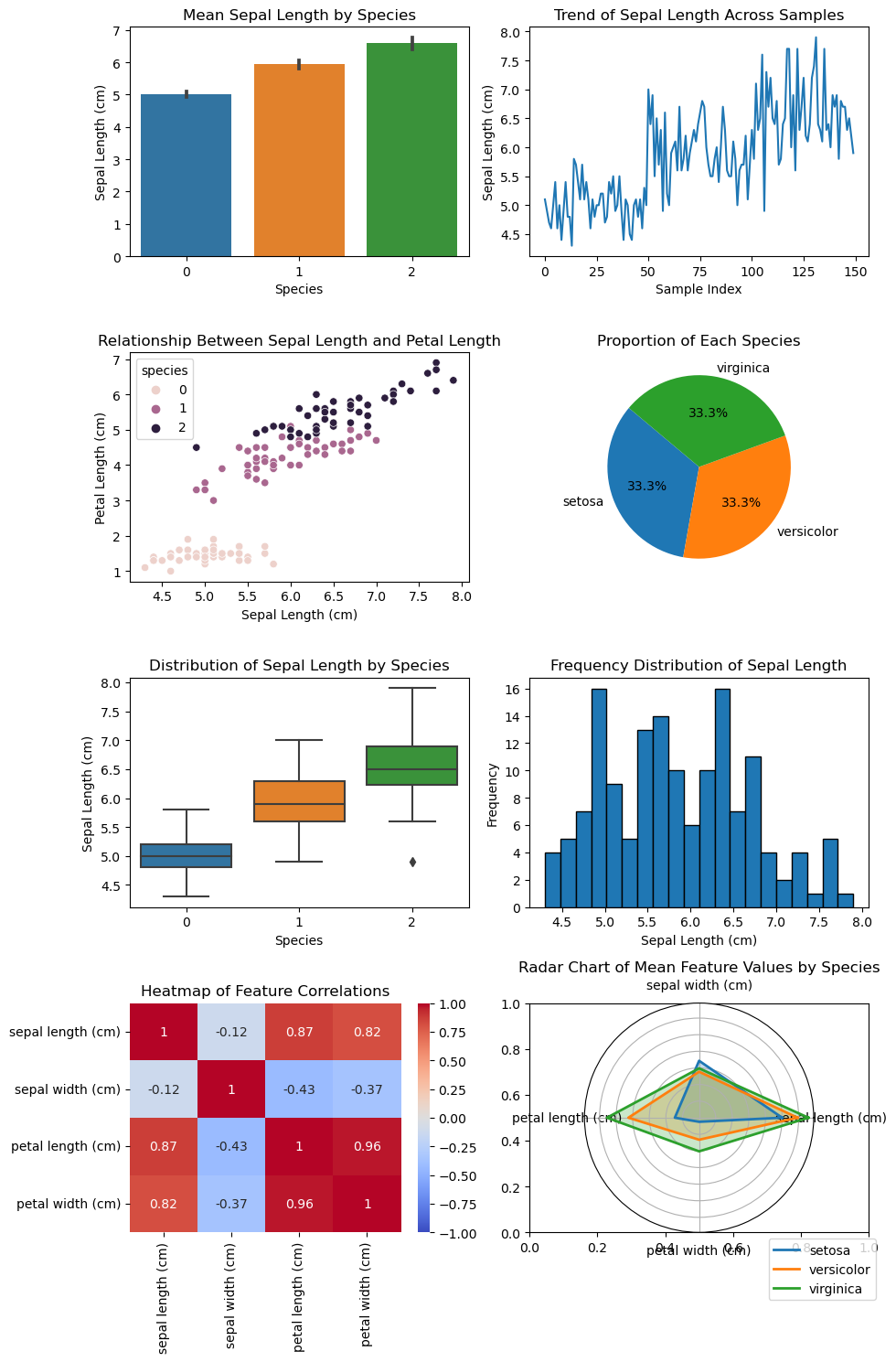
常见的数据图形化表示方式有很多,每种方式都适用于展示不同类型的数据和揭示不同的关系。以下是几种常见的数据图形化表示方式:
-
柱状图(Bar Chart):用于比较不同类别的数据值。
-
折线图(Line Chart):用于展示数据随时间的变化趋势。
-
散点图(Scatter Plot):用于展示两个变量之间的关系。
-
饼图(Pie Chart):用于展示数据在一个整体中的占比。
-
箱线图(Box Plot):用于展示数据的分布及其异常值,尤其适合展示四分位数。
-
直方图(Histogram):用于展示数据的频率分布。
-
热图(Heatmap):用于展示数值变量的密度分布。
-
雷达图(Radar Chart):用于展示多变量数据的比较。
每种图形化表示方式都有其独特的用途和优势,选择适合的图表类型可以更清晰地传达数据的含义。
import numpy as np
import pandas as pd
from scipy import stats
from sklearn.datasets import load_iris
# Load the Iris dataset
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
# Calculate statistics
statistics = {}
for column in df.columns:
data = df[column]
statistics[column] = {
'mean': np.mean(data),
'mode': stats.mode(data, keepdims=True)[0][0],
'median': np.median(data),
'quartiles': np.percentile(data, [25, 50, 75]),
'variance': np.var(data),
'standard_deviation': np.std(data),
'range': np.ptp(data),
'interquartile_range': stats.iqr(data)
}
# Convert statistics to DataFrame for better visualization
stats_df = pd.DataFrame(statistics).T
stats_df
| mean | mode | median | quartiles | variance | standard_deviation | range | interquartile_range | |
|---|---|---|---|---|---|---|---|---|
| sepal length (cm) | 5.843333 | 5.0 | 5.8 | [5.1, 5.8, 6.4] | 0.681122 | 0.825301 | 3.6 | 1.3 |
| sepal width (cm) | 3.057333 | 3.0 | 3.0 | [2.8, 3.0, 3.3] | 0.188713 | 0.434411 | 2.4 | 0.5 |
| petal length (cm) | 3.758 | 1.4 | 4.35 | [1.6, 4.35, 5.1] | 3.095503 | 1.759404 | 5.9 | 3.5 |
| petal width (cm) | 1.199333 | 0.2 | 1.3 | [0.3, 1.3, 1.8] | 0.577133 | 0.759693 | 2.4 | 1.5 |
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
from sklearn import datasets
# Load the iris dataset
iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['species'] = iris.target
# Plotting all charts as subplots in a single figure
fig, axes = plt.subplots(4, 2, figsize=(10, 15), subplot_kw=dict(polar=False))
# Bar Chart
sns.barplot(x='species', y='sepal length (cm)', data=df, ax=axes[0, 0])
axes[0, 0].set_title('Mean Sepal Length by Species')
axes[0, 0].set_xlabel('Species')
axes[0, 0].set_ylabel('Sepal Length (cm)')
# Line Chart
axes[0, 1].plot(df['sepal length (cm)'])
axes[0, 1].set_title('Trend of Sepal Length Across Samples')
axes[0, 1].set_xlabel('Sample Index')
axes[0, 1].set_ylabel('Sepal Length (cm)')
# Scatter Plot
sns.scatterplot(x='sepal length (cm)', y='petal length (cm)', hue='species', data=df, ax=axes[1, 0])
axes[1, 0].set_title('Relationship Between Sepal Length and Petal Length')
axes[1, 0].set_xlabel('Sepal Length (cm)')
axes[1, 0].set_ylabel('Petal Length (cm)')
# Pie Chart
species_counts = df['species'].value_counts()
axes[1, 1].pie(species_counts, labels=iris.target_names, autopct='%1.1f%%', startangle=140)
axes[1, 1].set_title('Proportion of Each Species')
# Box Plot
sns.boxplot(x='species', y='sepal length (cm)', data=df, ax=axes[2, 0])
axes[2, 0].set_title('Distribution of Sepal Length by Species')
axes[2, 0].set_xlabel('Species')
axes[2, 0].set_ylabel('Sepal Length (cm)')
# Histogram
axes[2, 1].hist(df['sepal length (cm)'], bins=20, edgecolor='k')
axes[2, 1].set_title('Frequency Distribution of Sepal Length')
axes[2, 1].set_xlabel('Sepal Length (cm)')
axes[2, 1].set_ylabel('Frequency')
# Heatmap
sns.heatmap(df.iloc[:, :-1].corr(), annot=True, cmap='coolwarm', vmin=-1, vmax=1, ax=axes[3, 0])
axes[3, 0].set_title('Heatmap of Feature Correlations')
# Radar Chart
# Create a subplot with polar coordinates for the radar chart
ax_radar = fig.add_subplot(4, 2, 8, polar=True)
# Calculate mean values for each species
mean_values = df.groupby('species').mean()
categories = list(mean_values.columns)
values = mean_values.values
# Number of variables
num_vars = len(categories)
# Compute angle for each axis
angles = np.linspace(0, 2 * np.pi, num_vars, endpoint=False).tolist()
angles += angles[:1]
# Plot data on the radar chart
for i, value in enumerate(values):
data = np.append(value, value[0])
ax_radar.plot(angles, data, linewidth=2, linestyle='solid', label=iris.target_names[i])
ax_radar.fill(angles, data, alpha=0.25)
# Set the axis labels
ax_radar.set_yticklabels([])
ax_radar.set_xticks(angles[:-1])
ax_radar.set_xticklabels(categories)
# Add title and legend
ax_radar.set_title('Radar Chart of Mean Feature Values by Species')
ax_radar.legend(loc='upper right', bbox_to_anchor=(1.3, 0))
plt.tight_layout()
plt.show()
 离散型概率分布
离散型概率分布
离散数据即数据的取值是不连续的。例如掷硬币就是一个典型的离散数据,因为抛硬币只有2种数值(也就是2种结果,要么是正面,要么是反面)。概率分布清楚而完整地表示了随机变量 $X$ 所取值的概率分布情况。离散型随机变量的概率分布可用表格形式来表示, 称之为分布列, 见下表。
$$
\begin{array}{|c|c|c|c|c|}
\hline X & x_1 & x_2 & \cdots & x_k \\
\hline P & p_1 & p_2 & \cdots & p_k \\
\hline
\end{array}
$$
离散型随机变量的概率分布列具有下列性质:
$$
\begin{aligned}
& \sum_{k=1}^{+\infty} p_k=1 \\
& p_k \geq 0, k=1,2, \cdots
\end{aligned}
$$
那么为什么要去统计概率分布呢?当统计学家们开始研究概率分布时,他们看到,有几种形状反复出现,于是就研究它们的规律,根据这些规律来解决特定条件下的问题。大家想想当年高考的时候,为了备战语文作文,可以准备一个自己的“万能模板”,任何作文题目都可以套用该模板,快速解决作文这个难题。同样的,记住概率里这些特殊分布的好处就是:下次遇到类似的问题,就可以直接套用“模板”(这些特殊分布的规律)来解决问题了。而这就是研究概率分布的意义所在。
两点分布
如果随机变量 $X$ 的分布列如下:
$$
\begin{aligned}
& P{X=1}=p(0<p<1) \\
& P{X=0}=q=1-p
\end{aligned}
$$
则称 $X$ 服从两点分布。两点分布也叫伯努利分布(Bernoulli)或 0-1 分布。
两点分布虽简单但很有用。当随机试验只有 2 个可能结果, 且都有正概率时, 就确定一个服从两点分布的随机变量。例如检查产品质量是否合格; 检查某车间的电力消耗是否超过负荷; 某射手对目标的一次射击是否中靶等试验都可以用服从二点分布的随机变量来描述。
二项分布
如果随机变量 $X$ 的概率分布为:
$$
P(X)=k=C_n^k p^k q^{n-k}, \mathrm{k}=0,1,2, \cdots, n, 0<p<1, q=1-p
$$
则称 $X$ 服从参数为 $n, p$ 的二项分布。其中, 二项定理的系数计算方法如下:
$$
C_n^k=\frac{n!}{k!(n-k)!}
$$
二项分布记为 $X \sim B(n, p)$ 或 $X \sim b(n, p)$ 。
-
服从二项分布的随机变量的直观背景可解释为:
- 重复服从二项分布的实验 $n$ 次, 某事件 $A$ 发生的次数 $X$ 是服从二项分布的随机变量。
-
二项分布有什么用呢?
- 假设遇到一个事情,如果该事情发生次数固定,而想要统计的是成功的次数,那么就可以用二项分布的公式快速计算出概率来。
-
如何判断是不是二项分布?
- 顾名思义,二项代表事件有2种可能的结果,把一种称为成功;另外一种称为失败。
- 生活中有很多这样2种结果的二项情况,例如表白结果是二项的,一种成功;另一种是失败。
-
二项分布符合下面4个特点:
- 做某件事的次数(也叫试验次数)是固定的,用n表示。
- 每一次事件都有两个可能的结果(成功,或者失败)。
- 每一次成功的概率都是相等的,成功的概率p用表示
- 感兴趣的是成功x次的概率是多少。
-
二项分布的期望
- $E(x)=n p$
- 表示某事情发生 $n$ 次, 预期成功多少次。
那么知道这个期望有什么用呢?
做任何事情之前, 知道预期结果肯定会对后面的决策有帮助。比如拋硬币 5 次, 每次概率是 $1 / 2$, 那么期望 $E(x)=5 \times \frac{1}{2}=2.5$ 次, 也就是有大约 3 次可以抛出正面。
再比如投资了 5 支股票,假设每支股票赚到钱的概率是 $80 \%$, 那么期望 $E(x)=5 \times 80 \%=4$, 也就是预期会有 4 只股票投资成功赚到钱。
几何分布
几何分布实际上与二项分布非常的像,先来看几何分布的4个特点:
- 做某件事的次数(也叫试验次数)是固定的,用n表示。
- 每一次事件都有两个可能的结果(成功,或者失败)。
- 每一次成功的概率都是相等的,成功的概率p用表示
- 感兴趣的是进行次尝试这个事情,取得第1次成功的概率是多大。
正如读者所看到的,几何分布和二项分布的区别只有第4点,也就是解决问题目的不同。几何分布的数学公式如下:
$$
p(x)=(1-p)^{x-1} p
$$
其中 $p$ 为成功概率, 即为了在第 $x$ 次尝试取得第 1 次成功, 首先要失败 $(x-1)$ 次。
继续刚才的例子,假如在表白之前, 计算出即使尝试表白 3 次, 在最后 1 次成功的概率还是小于 $50 \%$,还没有抛硬币的概率高。那就要考虑换个追求对象。或者首先提升下自己, 提高自己每一次表白的概率。
最后, 几何分布的期望是 $E(x)=1 / p$ 。假如每次表白的成功概率是 $60 \%$, 同时也符合几何分布的特点, 所以期望 $E(x)=1 / p=1 / 0.6=1.67$ 。这意味着表白 1.67 次(约等于 2 次)会成功。
泊松分布
如果随机变量$X$的概率分布为:
$$
P{X}=k=\frac{\lambda^k e^{-\lambda}}{k!}, k=0,1,2, \cdots
$$
其中常数 $\lambda>0$, 则称 $X$ 服从参数为 $\lambda$ 的泊松分布, 记为 $X \sim P(\lambda)$ 。 $k$ 代表事情发生的次数, $\lambda$ 代表给定时间范围内事情发生的平均次数。
-
那么泊松分布有什么用?
- 如果想知道某个时间范围内,发生某件事情$x$次的概率是多大。这时候就可以用泊松分布轻松搞定。
- 比如一天内中奖的次数,一个月内某机器损坏的次数等。
-
知道这些事情的概率有什么用呢?
*当然是根据概率的大小来做出决策了。比如组织一次抽奖活动,最后算出来一天内中奖10次的概率都超过了90%,然后进行期望和活动成本的比较,发现要赔不少钱,那这个活动就别组织了。
泊松分布符合以下3个特点:
- 事件是独立事件。
- 在任意相同的时间范围内,事件发的概率相同。
- 想知道某个时间范围内,发生某件事情次的概率是多大。
例如组织了一个促销抽奖活动, 只知道 1 天内中奖的平均个数为 4 个, 想知道 1 天内恰巧中奖次数为 8 的概率是多少?
$$
P(X)=8=\frac{4^8 e^{-4}}{8!}=0.0298
$$
泊松概率还有一个重要性质,它的数学期望和方差相等,都等于$\lambda$。
离散型数据分布小结
- 二点分布: 表示一次试验只有两种结果即随机变量 $X$ 只有两个可能的取值。
- 二项分布: 感兴趣的是成功 $x$ 次的概率是多少。
- 几何分布: 感兴趣的是进行 $x$ 次尝试这个事情, 取得第 1 次成功的概率是多大。
- 泊松分布: 想知道某个范围内, 发生某件事情 $x$ 次的概率是多大。
 连续型概率分布
连续型概率分布
概率密度函数
对于连续型随机变量,由于其取值不能一一列举出来,因而不能用离散型随机变量的分布列来描述其取值的概率分布情况。但人们在大量的社会实践中发现连续型随机变量落在任一区间 $[a, b]$ 上的概率, 可用某一函数 $f(x)$ 在 $[a, b]$ 上的定积分来计算。于是有下列定义:对于随机变量 $X$, 如果存在非负可积函数 $f(x)(-\infty<x<+\infty)$, 使对任意 $a, b(a<b)$ 都有 $P{a \leq X \leq b}=\int_a^b f(x) d x$ 。则称 $X$ 为连续型随机变量, 并称 $f(x)$ 为连续型随机变量 $X$ 的概率密度函数(Probability Density Function, PDF),简称概率密度或密度函数。
累积分布函数
不管 $X$ 是什么类型(连续/离散/其他)的随机变量, 都可以定义它的累积分布函数 $F_x(x)$ (cumulative distribution function, CDF), 有时简称为分布函数。对于连续性随机变量, CDF 就是 PDF 的积分, PDF 就是 CDF 的导数:
$$
F_X(x)=\operatorname{Pr}(X \leq x)=\int_{- \text {inf }}^x f_X(t) \mathrm{d} t
$$
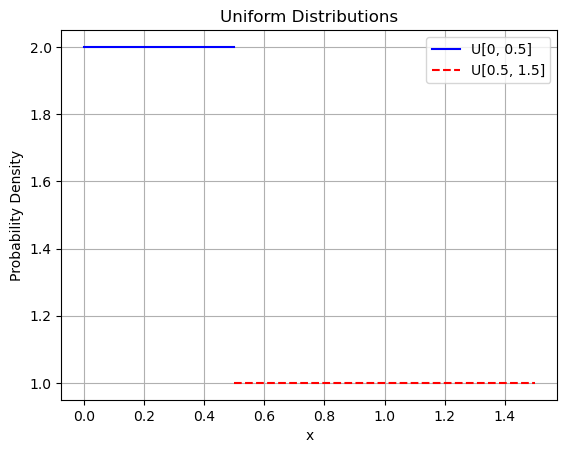
均匀(uniform)分布
设连续型随机变量 $X$ 在有限区间 $[a, b]$ 上取值, 且它的概率密度为:
$$
f(x)=\begin{cases}
\frac{1}{b-a} & a \leq x \leq b \\
0 & \text { 其它 }
\end{cases}
$$
则称 $X$ 服从区间 $[a, b]$ 上的均匀分布, 可记成 $X \sim U[a, b]$, 如图 1-32 所示。其中第一种分布使用实线表示, 范围为 $[0,0.5]$, 概率密度为 2 ; 第二种分布使用虚线表示, 范围为 $[0.5,1.5]$,概率密度为 1 。
import numpy as np
import matplotlib.pyplot as plt
# Define the ranges for the two distributions
x1 = np.linspace(0, 0.5, 100)
x2 = np.linspace(0.5, 1.5, 100)
# Define the probability densities
f1 = np.full_like(x1, 2) # Probability density for first distribution
f2 = np.full_like(x2, 1) # Probability density for second distribution
# Plot the first distribution
plt.plot(x1, f1, label='U[0, 0.5]', color='blue')
# Plot the second distribution
plt.plot(x2, f2, label='U[0.5, 1.5]', color='red', linestyle='dashed')
# Add labels and legend
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Uniform Distributions')
plt.legend()
plt.grid(True)
plt.show()
例: 设公共汽车每隔 5 分钟一班, 乘客到站是随机的, 则等车时间 $X$ 服从 [0,5]上的均匀分布, 求 $X$ 的密度函数并求某乘客随机地去乘车而候车时间不超过 3 分钟的概率?
解: $X$ 服从 $[0,5]$ 上的均匀分布, 故其密度函数为:
$$
f(x)=\begin{cases}
\frac{1}{5} & 0 \leq x \leq 5 \\
0 & \text { 其它 }
\end{cases}
$$
候车时间不超过 3 分钟的概率为:
$$
P{0 \leq X \leq 3}=\int_0^3 \frac{1}{5} d x=\frac{3}{5}
$$
指数(exponential)分布
指数分布可以用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔等。 许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可用指数分布来近似。它在可靠性研究中是最常用的一种分布形式。
设连续型随机变量$X$的概率密度为:
$$
f(x)=\begin{cases}
\lambda e^{-\lambda x} & x \geq 0 \\
0 & x<0
\end{cases}
$$
其中常数 $\lambda>0$, 则称 $X$ 服从参数为 $\lambda$ 的指数分布, 可记成 $X \sim E(\lambda)$
如下图所示。其中第一种分布使用实线表示 $(\lambda=2)$; 第二种分布使用虚线表示 $(\lambda=1)$ 。
import numpy as np
import matplotlib.pyplot as plt
# Define the exponential distribution functions
def exponential_pdf(x, lambda_):
return lambda_ * np.exp(-lambda_ * x)
# Define the range for x
x = np.linspace(0, 5, 1000)
# Define the lambda values
lambda_1 = 2
lambda_2 = 1
# Calculate the probability densities
y1 = exponential_pdf(x, lambda_1)
y2 = exponential_pdf(x, lambda_2)
# Plot the first distribution
plt.plot(x, y1, label=r'$\lambda=2$', color='blue')
# Plot the second distribution
plt.plot(x, y2, label=r'$\lambda=1$', color='red', linestyle='dashed')
# Add labels and legend
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Exponential Distributions')
plt.legend()
plt.grid(True)
plt.show()
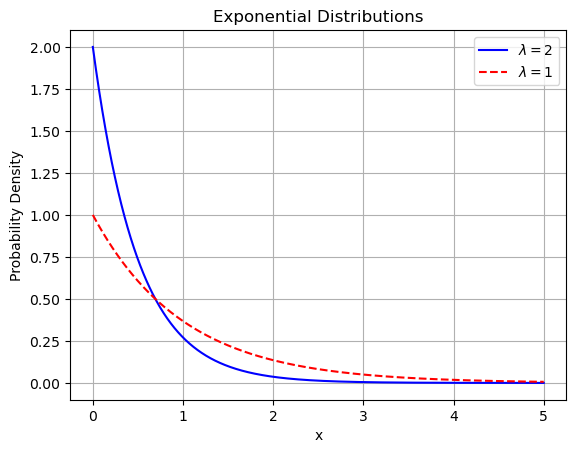
例: 设某人造卫星的寿命 $X$ (单位: 年)服从参数为 $2 / 3$ 的指数分布。若 3 颗这样的卫星同时升空投入使用, 求 2 年后 3 颗卫星都正常运行的概率?
解: $X$ 的密度函数为:
$$
f(x)=\begin{cases}
\frac{2}{3} \mathrm{e}^{-\frac{2}{3} x} & x \geq 0 \\
0 & x<0
\end{cases}
$$
故 1 颗卫星 2 年后还正常运行的概率为:
$$
P{X \geq 2}=\int_2^{+\infty} \frac{2}{3} \mathrm{e}^{-\frac{2}{3} x} \mathrm{~d} x=\mathrm{e}^{-\frac{4}{3}}
$$
因此, 2 年后 3 颗卫星都正常的概率为:
$$
P{Y=3}=\left(\mathrm{e}^{-\frac{4}{3}}\right)^3=\mathrm{e}^{-4} \approx 0.0183
$$
正态分布
正态分布又名高斯分布,是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。若连续型随机变量 $X$ 的密度函数为:
$$
f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right),-\infty<x<+\infty
$$
其中, $\mu$ 为均值、 $\sigma$ 为标准差, $\mu, \sigma(\sigma>0)$ 都为常数, 则称 $X$ 服从参数为 $\mu, \sigma$ 的正态分布,简记为 $X \sim N\left(\mu, \sigma^2\right)$ 。因其曲线呈钟形, 因此又经常称之为钟形曲线。通常所说的标准正态分布是 $\mu=0, \sigma=1$ 的正态分布。
正态分布的参数中, $\mu$ 决定了其位置, 标准差 $\sigma^2$ 决定了分布的幅度。
具体来说, 若固定 $\sigma$ 而改变 $\mu$ 的值, 则正态分布密度曲线沿着 $x$ 轴平行移动, 而不改变其形状, 可见曲线的位置完全由参数 $\mu$ 确定。
若固定 $\mu$ 而改变 $\sigma$ 的值, 则当 $\sigma$ 越小时图形变得越陡峭; 反之,当 $\sigma$ 越大时图形变得越平缓,
如下图所示。其中第一种分布使用实线表示 $(\mu=0, \sigma=0.5$ );第二种分布使用虚线表示 $(\mu=1, \sigma=1)$ 。
import numpy as np
import matplotlib.pyplot as plt
# Define the normal distribution function
def normal_pdf(x, mu, sigma):
return (1 / (sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma)**2)
# Define the range for x
x = np.linspace(-3, 5, 1000)
# Parameters for the normal distributions
mu1, sigma1 = 0, 0.5
mu2, sigma2 = 1, 1
# Calculate the probability densities
y1 = normal_pdf(x, mu1, sigma1)
y2 = normal_pdf(x, mu2, sigma2)
# Plot the first distribution
plt.plot(x, y1, label=r'$\mu=0, \sigma=0.5$', color='blue')
# Plot the second distribution
plt.plot(x, y2, label=r'$\mu=1, \sigma=1$', color='red', linestyle='dashed')
# Add labels and legend
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Normal Distributions')
plt.legend()
plt.grid(True)
plt.show()
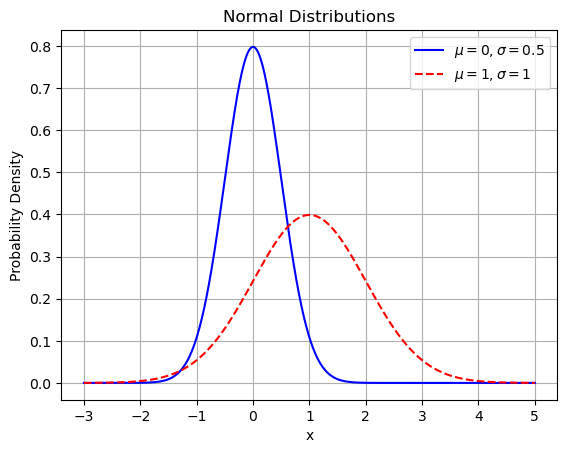
正态分布中一些值得注意的量:
- 密度函数关于平均值对称。
- 平均值与它的众数以及中位数同一数值。
- 68.268949%的面积在平均数左右的一个标准差范围内。
- 95.449974%的面积在平均数左右两个标准差的范围内。
- 99.730020%的面积在平均数左右三个标准差的范围内。
- 99.993666%的面积在平均数左右四个标准差的范围内。
在实际应用上,常考虑一组数据具有近似于正态分布的概率分布。
若其假设正确,则约68.3%数值分布在距离平均值有1个标准差之内的范围,约95.4%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。
称为“68-95-99.7法则”或“经验法则”。
Z值与标准化
可以通过计算随机变量的Z值(z-score),得知其距离均值有多少个标准差。Z值的计算公式为:
$$
\mathrm{Z}=\frac{x-\mu}{\sigma}
$$
其中 $x$ 是随机变量的值, $\mu$ 是总体均值, $\sigma$ 是总体标准差。当 $\mu=0, \sigma=1$ 时, 正态分布就成为标准正态分布, 记作 $N(0,1)$ 。 $\mathrm{Z}$ 值将两组或多组数据转化为无单位的 $\mathrm{Z}$ score 分值, 使得数据标准统一化, 提高了数据可比性, 同时也削弱了数据解释性。 $\mathrm{z}$ 值的量代表着实测值和总体平均值之间的距离, 是以标准差为单位计算。大于均值的实测值会得到一个正数的 $\mathrm{z}$ 值,小于均值的实测值会得到一个负数的 $\mathrm{z}$ 值。
数据分析与挖掘中,很多方法需要样本符合一定的标准,如果需要分析的诸多自变量不是同一个量级,就会给分析工作造成困难,甚至影响后期建模的精准度。举个例子:
- 假设:A班级的平均分是80,标准差是10,A考了90分;B班的平均分是400,标准差是100,B考了600分。A和B谁的成绩好?
- 这可以计算得出,A的Z-score是(90-80)/10=1,B的Z-score(600-400)/100=2是。因此B的成绩更为优异。
通过Z-score可以有效的把数据转换为统一的标准,并进行比较。但是需要注意,Z-score本身没有实际意义,它的现实意义需要在比较中得以实现,这也是Z-score的缺点之一。
Z-score的另一个缺点是估算Z-score需要总体的平均值与方差,但是这一值在真实的分析与挖掘中很难得到,大多数情况下是用样本的均值与标准差替代。
正态分布为什么如此重要?
正态分布是最常见也是最重要的一种分布,自然界及社会生活、生产实际中很多随机变量都服从或近似服从正态分布,例如产品的各种质量指标、测量误差、某地区的年降雨量和成年人的身高等。
-
一个经典的例子是高尔顿顶板:
-
高尔顿顶板由一个垂直放置的板子构成,板子上有许多水平排列的小钉子,钉子之间有一定间隔。板子的顶部有一个漏斗,用于让小球(通常是钢珠)通过。小球从漏斗口依次落下,碰到钉子后随机地向左或向右弹跳,继续向下掉落,直到到底部的多个格子中。
-
当大量小球从漏斗中落下时,它们经过钉子的随机弹跳后,最终落在每个格子中的小球数量形成了一个钟形曲线,即正态分布。
-
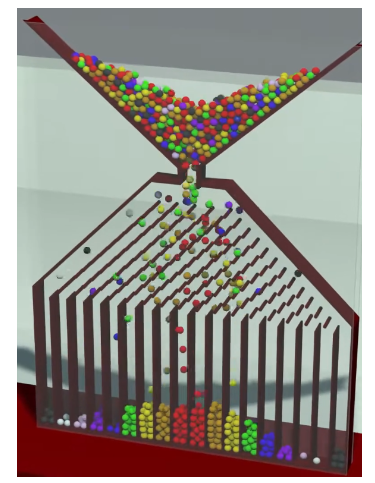
- 高尔顿顶板的关键点:
- 当小球数量足够大时,个体行为的随机性被群体行为的稳定性所覆盖,形成了有规律的分布。这被称为大数定律
- 无论小球的初始分布如何,当其经过多次独立的随机过程后,最终的分布趋向于正态分布。这是正态分布在统计学和自然现象中如此普遍的重要原因。这被称为中心极限定理
大数定律与中心极限定理是统计学家总结出的自然现象,是概率统计的基石。很多定理和推论都是基于它们之上的研究。
 统计学
统计学
统计学旨在根据数据样本推测总情况。大部分统计分析都基于概率,所以这两方面的内容通常兼而有之。
统计推断是依据从总体中抽取的一个简单随机样本对总体进行分析和判断。
统计推断的基本问题可以分为两大类:
- 一类是参数估计问题
- 点估计
- 区间估计
- 一类是假设检验问题
- 假设性检验
- 相关性分析
 点估计
点估计
参数是指总体分布中的未知参数。例如, 在正态总体 $N\left(\mu, \sigma^2\right)$ 中, $\mu, \sigma^2$ 未知, $\mu$ 与 $\sigma^2$ 就是参数; 若在指数分布 $E(\lambda)$ 的总体中, $\lambda$ 未知, 则 $\lambda$ 是参数。
-
所谓参数估计就是由样本值对总体的未知参数作出估计。
-
点估计:点估计是通过样本数据计算一个单一值来估计总体的未知参数。
-
区间估计:区间估计是通过样本数据计算一个范围,用于包含总体未知参数的可能值,并提供一个置信水平。
-
构造点估计的一个经典常用方法是最大似然估计法
在统计学中,我们经常需要从样本数据推断总体参数。极大似然估计是一种通过最大化似然函数来估计未知参数的方法。其核心思想是寻找使样本数据最可能出现的参数值。
极大似然估计的目标是通过样本数据找到一组参数,使得在这组参数下,数据出现的概率最大。
假设我们有一个样本 $X=\left(X_1, X_2, \ldots, X_n\right)$ ,其观测值来自一个未知参数为 $\theta$ 的概率分布 $f(x ; \theta)$ 。极大似然估计的步骤如下:
-
构建似然函数:似然函数 $L(\theta)$ 是给定样本数据 $X$ 的情况下,参数 $\theta$ 的概率。对于独立同分布的样本,似然函数可以表示为:
$$
L(\theta)=\prod_{i=1}^n f\left(x_i ; \theta\right)
$$ -
构建对数似然函数:由于似然函数是多个概率的乘积,计算上可能会出现数值下溢的问题。因此,通常使用对数似然函数 $l(\theta)$ :
$$
l(\theta)=\log L(\theta)=\sum_{i=1}^n \log f\left(x_i ; \theta\right)
$$ -
求解最大化问题: 找到使对数似然函数 $l(\theta)$ 最大的参数 $\theta$ ,即:
$$
\hat{\theta}=\arg \max _\theta l(\theta)
$$
在实际应用中,求解极大似然估计的问题通常涉及到以下步骤:
step 1 选择合适的假定分布或模型
首先,我们需要选择一个概率分布模型 $f(x; \theta)$,这个模型应能够合理地描述我们数据的分布。常见的模型包括:
- 正态分布: 适用于数据呈现出对称的钟形曲线的情况。
- 指数分布: 常用于描述寿命数据或时间间隔数据。
- 泊松分布: 适用于计数数据,比如单位时间内的事件发生次数。
假定的选择很大程度上取决于数据的特性和领域知识。
如果实在没办法确定假定分布,实际上也可以通过不同的模型来拟合$f$。根据具体的应用场景和数据的特点,我们可以选择以下几种常见的模型来描述 $f(x ; \theta)$。
- 线性模型
- 神经网络
- 混合模型
- 等等...
step 2 构建对数似然函数
假设我们选择了一个合适的概率分布 $f(x ; \theta)$,然后我们基于这个分布构建似然函数:
$$
L(\theta)=\prod_{i=1}^n f\left(x_i ; \theta\right)
$$
这个似然函数 $L(\theta)$ 表示在给定参数 $\theta$ 下,观测到样本数据 $X$ 的可能性。
由于直接使用似然函数进行计算可能会面临数值稳定性问题(如下溢),我们通常使用对数似然函数 $l(\theta)$ 进行计算,通过对数变换,原来的乘积形式变为加法形式,极大地简化了计算。
step 3 求解对数似然函数的极值
-
为了找到参数 $\theta$ 使得对数似然函数 $l(\theta)$ 最大化,我们通常需要对其进行求导,然后解出导数等于零的点,即找到 $l(\theta)$ 的驻点。
-
我们通过对 $\theta$ 求偏导数 $\frac{\partial l(\theta)}{\partial \theta}$ ,并令其等于零,得到一组方程。通过解这些方程,我们可以得到参数 $\theta$ 的估计值 $\hat{\theta}$ 。
-
对于简单的分布,解析求解导数方程可能是可行的。然而,在许多情况下,尤其是模型比较复杂或者参数维度较高时,解析求解变得非常困难。因此,我们通常采用数值优化方法来求解这些方程。
-
此时,会将求解极大似然问题,等价转换成求解负对数似然的极小值问题,即优化问题。负对数似然函数形式如下:
$$
-l(\theta)=-\sum_{i=1}^n \log f\left(x_i ; \theta\right)
$$
通过最小化这个负对数似然函数,我们可以找到使样本数据出现概率最大的参数 $\theta$。 常用的优化算法包括:梯度下降法,牛顿法,EM算法等,我们将在其他章节里详细介绍
对数边际似然(Log Marginal Likelihood)
它表示在给定模型参数下观测数据的总体概率。为了更好地理解对数边际似然,可以将其与极大似然估计进行对比和解释。
边际似然是通过对参数的联合分布积分得到的,其目标是计算观测数据 $X$ 的整体概率 $P(X)$ 。
对数边际似然定义为:
$$
\log P(X)=\log \int P(X \mid \theta) P(\theta) d \theta
$$
这个积分考虑了所有可能的参数值及其先验概率,表示在模型下观测到数据 $X$ 的总概率。
极大似然估计 vs. 对数边际似然
-
极大似然估计 (MLE):最大化给定参数下观测数据的似然。它不考虑参数的先验分布,只关注找到最可能的参数值:
$$
\hat{\theta}_{\mathrm{MLE}}=\arg \max _\theta \log P(X \mid \theta)
$$ -
对数边际似然:考虑了参数的先验分布,通过对所有可能的参数值进行积分计算观测数据的整体概率:
$$
\log P(X)=\log \int P(X \mid \theta) P(\theta) d \theta
$$
从计算复杂性来说:
- 极大似然估计:通常通过优化算法直接找到使对数似然最大的参数值,计算相对简单。
- 对数边际似然:需要对参数空间进行积分,计算复杂且通常不可行,特别是在高维参数空间中。
蒙特卡洛采样(Monte Carlo Sampling)
由于对数边际似然涉及对高维参数空间进行积分,直接计算通常是不可行的。为了解决这一问题,可以引入蒙特卡洛采样方法。蒙特卡洛采样是一种通过随机样本估计复杂积分的数值方法,广泛应用于统计学和机器学习中。
蒙特卡洛采样的基本步骤如下
原来的积分可以写成期望的形式 $\int p(x \mid z ; \theta) p(z) \mathrm{d} z=\mathbb{E}_{z \sim p(z)}[p(x \mid z ; \theta)]$, 然后利用期望法求积分, 步骤如下。
(1) 从 $p(z)$ 中多次采样 $z_1, z_2, \cdots, z_m$ ;
(2) 根据 $p(x \mid z ; \theta)$ 计算 $x_1, x_2, \cdots, x_m$
(3) 求 $x$ 的均值。用数学表达为:
$$
\int p(x \mid z ; \theta) p(z) \mathrm{d} z=\mathbb{E}_{z \sim p(z)}[p(x \mid z ; \theta)] \approx \frac{1}{m} \sum_{j=1}^m p\left(x_j \mid z_j ; \theta\right)
$$
通过对 $z$ 多次采样,可以计算 $\nabla_\theta L(\theta ; X)$ 的近似值。
简单来说, 蒙特卡洛采样就是通过样本的均值来近似总体的积分。
 示例:线性回归模型的极大似然求解
示例:线性回归模型的极大似然求解
假设我们的线性模型是:
$$
y_i=\theta^T x_i+\epsilon_i
$$
其中,$\theta$ 是我们需要估计的参数向量,$x_i$ 是自变量,$y_i$ 是因变量,$\epsilon_i$ 是误差项。假设误差项 $\epsilon_i$ 独立同分布且服从均值为零、方差为 $\sigma^2$ 的正态分布,即:
$$
\epsilon_i \sim \mathcal{N}\left(0, \sigma^2\right)
$$
这意味着,对于每一个观测值 $y_i$,条件概率密度函数为:
$$
f\left(y_i \mid x_i ; \theta, \sigma^2\right)=\frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{\left(y_i-\theta^T x_i\right)^2}{2 \sigma^2}\right)
$$
这是因为我们假设误差项 $\epsilon_i$ 服从正态分布,而 $y_i$ 是 $\theta^T x_i$ 和误差项 $\epsilon_i$ 的线性组合。由于正态分布的线性组合仍然是正态分布,因此 $y_i$ 在给定 $x_i$ 的情况下,服从均值为 $\theta^T x_i$、方差为 $\sigma^2$ 的正态分布。参考下述正态分布的公式,可构建上式:
$$
f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right)
$$
由于乘法形式的似然函数在计算上可能会遇到数值下溢的问题,我们通常采用对数似然函数。对数似然函数 $l(\theta, \sigma^2)$ 是似然函数 $L(\theta, \sigma^2)$ 的对数:
$$
l\left(\theta, \sigma^2\right)=\log \left(\prod_{i=1}^n \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{\left(y_i-\theta^T x_i\right)^2}{2 \sigma^2}\right)\right)
$$
$$
l\left(\theta, \sigma^2\right)=\sum_{i=1}^n \log \left(\frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{\left(y_i-\theta^T x_i\right)^2}{2 \sigma^2}\right)\right)
$$
利用对数的性质 $\log(ab) = \log a + \log b$ 和 $\log(a^b) = b \log a$,对上式进行简化:
$$
l\left(\theta, \sigma^2\right)=\sum_{i=1}^n\left(\log \frac{1}{\sqrt{2 \pi \sigma^2}}+\log \exp \left(-\frac{\left(y_i-\theta^T x_i\right)^2}{2 \sigma^2}\right)\right)
$$
首先,处理常数项:
$$
\log \frac{1}{\sqrt{2 \pi \sigma^2}}=-\frac{1}{2} \log \left(2 \pi \sigma^2\right)
$$
接下来,处理指数项的对数:
$$
\log \exp \left(-\frac{\left(y_i-\theta^T x_i\right)^2}{2 \sigma^2}\right)=-\frac{\left(y_i-\theta^T x_i\right)^2}{2 \sigma^2}
$$
将这两部分结合,我们得到:
$$
l\left(\theta, \sigma^2\right)=\sum_{i=1}^n\left(-\frac{1}{2} \log \left(2 \pi \sigma^2\right)-\frac{\left(y_i-\theta^T x_i\right)^2}{2 \sigma^2}\right)
$$
-
注意,上述推导的最后结果中,带有参数 $\theta^T$ 的项,实际上就是MSE!
-
在后续的学习中,MSE经常作为深度学习模型的损失函数,来衡量模型的预测结果和真值,其本质原理实际上就是极大似然估计!
 示例:生成模型的对数边界似然求解
示例:生成模型的对数边界似然求解
假设我们有一个简单的生成模型,用于生成数据 $X$ 。生成模型的参数为 $\theta$ ,我们希望估计这些参数使得模型能够很好地生成观测数据。
生成模型的定义
假设观测数据 $X$ 是由潜在变量 $Z$ 生成的。模型参数 $\theta$ 控制生成过程。假设潜在变量 $Z$ 服从均值为 $\mu$ 方差为 $\sigma^2$ 的正态分布:
$$
Z \sim \mathcal{N}\left(\mu, \sigma^2\right)
$$
观测数据 $X$ 在给定潜在变量 $Z$ 和参数 $\theta$ 的情况下,服从均值为 $f(Z ; \theta)$ 、方差为 $\sigma^2$ 的正态分布:
$$
X \mid Z, \theta \sim \mathcal{N}\left(f(Z ; \theta), \sigma^2\right)
$$
边际似然和对数边际似然
我们感兴趣的是观测数据 $X$ 的边际似然 $P(X)$ ,它可以通过对潜在变量 $Z$ 的联合分布进行积分得到:
$$
P(X)=\int P(X \mid Z, \theta) P(Z) d Z
$$
对数边际似然(Log Marginal Likelihood)则是边际似然的对数:
$$
\log P(X)=\log \int P(X \mid Z, \theta) P(Z) d Z
$$
对数边际似然的推导
- 联合分布:
首先,我们需要知道观测数据 $X$ 和潜在变量 $Z$ 的联合分布 $P(X, Z \mid \theta)$ :
$$
P(X, Z \mid \theta)=P(X \mid Z, \theta) P(Z)
$$
由于 $Z$ 服从正态分布 $\mathcal{N}\left(\mu, \sigma^2\right)$ ,我们有:
$$
P(Z)=\frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(Z-\mu)^2}{2 \sigma^2}\right)
$$
同时,由于 $X \mid Z, \theta$ 服从均值为 $f(Z ; \theta)$ 、方差为 $\sigma^2$ 的正态分布,我们有:
$$
P(X \mid Z, \theta)=\frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(X-f(Z ; \theta))^2}{2 \sigma^2}\right)
$$
因此,联合分布可以写成:
$$
P(X, Z \mid \theta)=\left(\frac{1}{\sqrt{2 \pi \sigma^2}}\right)^2 \exp \left(-\frac{(X-f(Z ; \theta))^2+(Z-\mu)^2}{2 \sigma^2}\right)
$$
- 对数边际似然:
为了得到边际似然 $P(X)$ ,我们需要对潜在变量 $Z$ 积分:
$$
P(X)=\int P(X \mid Z, \theta) P(Z) d Z=\int\left(\frac{1}{\sqrt{2 \pi \sigma^2}}\right)^2 \exp \left(-\frac{(X-f(Z ; \theta))^2+(Z-\mu)^2}{2 \sigma^2}\right)
$$
对数边际似然是边际似然的对数:
$$
\log P(X)=\log \int\left(\frac{1}{\sqrt{2 \pi \sigma^2}}\right)^2 \exp \left(-\frac{(X-f(Z ; \theta))^2+(Z-\mu)^2}{2 \sigma^2}\right) d Z
$$
这个积分通常是复杂且难以解析求解的。
由于直接计算对数边际似然通常不可行,我们使用变分推断方法进行近似。详见信息论教程
 区间估计
区间估计
-
点估计值经常有差异。为了解决这个问题,有了区间估计的做法。通俗地讲:区间估计是在点估计的基础上,给一个合理取值范围。
-
比如:抽样鸡腿的平均重量为150克,是一个点估计值。抽样鸡腿的平均重量为145克到155克之间,是一个区间估计。
- 其中,145到155称为置信区间。这很符合人们的常规理解:东西很难100%准确,有个范围也是可以理解的。
-
但这个范围有多大可信度呢?
- 通常用置信水平来衡量,即:“有多大把握,真实值在置信区间内”。一般用 $(1-\alpha)$ 表示。如果 $\alpha$ 取 0.05 , 则置信水平为 0.95 , 即 $95 \%$ 的把握。 $\alpha$ 指的是显著性水平。
- 置信区间与置信水平连起来,完整的表达为:“有95%(置信水平)的把握,鸡腿平均重量在145至155克之间(置信区间)。”
-
有小伙伴会好奇,为什么置信水平不是100%!
- 通俗地说,当置信水平太高时,置信区间会变得非常大,从而产生一些正确但无用的结论。
 假设性检验
假设性检验
-
假设检验的目的与参数估计的目的相同,都是根据样本求总体的参数。
-
但是思想正好相反:可以把参数估计看作正推,即根据样本推测总体;而假设检验是反证,即先在总体上作某项假设,用从总体中随机抽取的一个样本来检验此项假设是否成立。
-
假设检验可分为两类:
- 一类是总体分布形式已知,为了推断总体的某些性质,对其参数作某种假设,一般对数字特征作假设,用样本来检验此项假设是否成立,称此类假设为参数假设检验。
- 另一类是总体形式未知,对总体分布作某种假设。例如,假设总体服从泊松分布,用样本来检验假设是否成立,称此类检验为分布假设检验。
-
假设检验依据的是小概率思想,即小概率事件在一次试验中基本上不会发生。
-
如果样本数据拒绝该假设,那么说明该假设检验结果具有统计显著性。一项检验结果在统计上是“显著的”,意思是指样本和总体之间的差别不是由于抽样误差或偶然而造成的,而是设立的假设错误。
-
其实这个思想前人早就有过总结:事出反常必为妖。
-
假设检验的常见术语:
-
(1)零假设(null hypothesis):是试验者想收集证据予以反对的假设,也称为原假设,通常记为$H_0$。例如:零假设是检验“样本的均值不等于总体均值”这一观点是否成立。
-
(2)备择假设(alternative hypothesis):是试验者想收集证据予以支持的假设,通常记为$H_1$。例如:备择假设是检验“样本的均值等于总体均值”这一观点是否成立。
-
(3)双尾检验(two-tailed test):如果备择假设没有特定的方向性,并含有符号“=/”,这样的检验称为双尾检验。例如上面给出的零假设和备择假设的例子。
-
(4)单尾检验(one-tailed test):如果备择假设具有特定的方向性,并含有符号“>”或“<”,这样的检验称为单尾检验。单尾检验分为左尾(lower tail)和右尾(upper tail)。 例如:零假设是检验“样本的均值小于等于总体均值”,备择假设是检验“样本的均值大于总体均值”。
-
(5)第I类错误(弃真错误):意思是零假设为真时错误地拒绝了零假设。犯第I类错误的最大概率记为 $\alpha$。
-
(6)第II类错误(取伪错误):意思是零假设为假时错误地接受了零假设。犯第II类错误的最大概率记为 $\beta$。
-
(7)检验统计量(test statistic):用于假设检验计算的统计量。例如:Z值、t值、f值和卡方值。
-
(8)显著性水平(level of significance):当零假设为真时,错误拒绝零假设的临界概率,即犯第一类错误的最大概率,用$\alpha$表示。显著性水平一般根据正态分布的经验法则(68%、95%、99%)进行选取,例如:在5%(1-95%)的显著性水平下,样本数据拒绝原假设。
-
(9)置信度(confidence level):置信区间包含总体参数的确信程度,即$1-\alpha$。例如:95%的置信度表明,有95%的确信度相信置信区间包含总体参数。
-
(10)置信区间(confidence interval):包含总体参数的随机区间。
-
(11)功效(power):正确拒绝零假设的概率($1-\beta$),即不犯二类错误的概率。
-
(12)临界值(critical value):与检验统计量的具体值进行比较的值。是在概率密度分布图上的分位数。这个分位数在实际计算中比较麻烦,它需要对数据分布的密度函数积分来获得。
-
(13)临界区域(critical region):拒绝原假设的检验统计量的取值范围,也称为拒绝域(rejection region),是由一组临界值组成的区域。如果检验统计量在拒绝域内,那么拒绝原假设。
-
-
假设检验的一般步骤
- (1)定义总体。
- (2)确定原假设和备择假设。
- (3)选择检验统计量(研究的是统计量:值、值、值和卡方值)。
- (4)选择显著性水平(一般约定俗成的定义为0.05)。
- (5)从总体进行抽样,得到一定的数据。
- (6)根据样本数据计算检验统计量的具体值。
- (7)依据所构造的检验统计量的抽样分布和显著性水平,确定临界值和拒绝域。
- (8)比较检验统计量的值与临界值,如果检验统计量的值在拒绝域内,则拒绝原假设。
例:
某茶叶厂用自动包装机将茶叶装袋。每袋的标准质量规定为100 g。每天开工时,需要检验一下包装机工作是否正常。根据以往的经验知道,用自动包装机装袋质量服从正态分布,装袋质量的标准差$\sigma=1.15(\mathrm{~g})$。
某日开工后,抽测了9袋,其质量如下(单位:g):
99.3,98.7,100.5,101.2,98.3,99.7,99.5,102.1,100.5。
试问此包装机工作是否正常?
-
解法如下:
- 设茶叶装袋质量为 $X \mathrm{~g}, X \sim N\left(\mu, 1.15^2\right)$ 。
- 现在的问题是茶叶袋的平均质量是否为 $100 \mathrm{~g}$
- 即原假设 $\mu=100$, 记作 $\mathrm{H} 0: \mu=100$,
- 记备择假设 $\mathrm{H} 1: \mu \neq 0$ 。
如果这个假设 $\mathrm{H} 0$ 成立, 则 $X \sim N\left(100,1.15^2\right)$ 。
-
取统计量z值:
$$
U=\frac{\bar{X}-100}{1.15 / \sqrt{9}}
$$ -
根据中心法则和 $\mathrm{z}$ 值的定义, 这个统计量服从标准正态分布, 即:
$$
U=\frac{\bar{X}-100}{1.15 / \sqrt{9}} \sim N(0,1)
$$ -
定义一个选择显著性水平, 比如 $\alpha=0.05$, 当事件的发生概率小于这个值时, 则事件是一个小概率事件。
-
根据标准正态分布的概率密度表查得 $u_{0.025}=1.96$, 又 $\bar{x}=99.98$,得统计量 $U$ 的观测值:
$$
u=\frac{\bar{x}-100}{1.15 / \sqrt{9}}=-0.052
$$
由于 $|u|=0.052<1.96$, 所以小概率事件$\lbrace\left|\frac{\bar{X}-100}{1.15 / \sqrt{9}}\right| \geq u_{0.025}\rbrace$ 没有发生, 因此可认为原来的假设 $\mathrm{H} 0$ 成立, 即: $\mu=100$ 。
P值的定义
在统计假设检验中,P值(或概率值)是用于衡量观察到的数据在原假设成立时出现的概率。具体来说,P值表示在原假设为真时,观察到比当前结果更极端(更偏离原假设)的结果的概率。
P值的解释
在这个例子中:
- 原假设 $\left(\mathrm{H}_0\right): \mu=100$ (即包装机装袋的平均质量为 100 克)。
- 备择假设 $\left(\mathrm{H}_1\right): \mu \neq 100$ (即包装机装袋的平均质量不等于 100 克)。
我们已经计算了样本均值 $\bar{x}=99.98$ 和统计量 $U$ 的观测值:
$$
u=\frac{\bar{x}-100}{1.15 / \sqrt{9}}=-0.052
$$
接下来,我们需要确定 P值。 计算 P值的具体步骤如下:
- 计算观测值 $u=-0.052$ 对应的累计概率。
- 查找标准正态分布表,或者使用统计软件/计算器,找到 $u=-0.052$ 的累积概率。
假设我们使用统计软件或表格,我们可以找到:
$$
P(Z \leq-0.052) \approx 0.4807
$$
由于这是一个双尾检验,我们还需要考虑正尾部分:
$$
P(Z \geq 0.052) \approx 0.4807
$$
因此,总的 P值为:
$$
P=2 \times 0.4807=0.9614
$$
在这个例子中, 假设包装机工作正常,即平均装袋质量确实是 100 克。
-
P 值表示的概率:P 值 0.9614 表示,如果包装机的平均装袋质量确实是 100 克,那么我们会观察到像 99.98 克这样或者比这更偏离 100 克的样本均值的概率是 96.14%。
-
通常我们选择的显著性水平是 $\alpha=0.05$ (即 $5 \%$ )。这意味着我们希望有小于 $5 \%$的概率才会拒绝原假设,因为这样的概率被认为是“显著”的小概率事件。
-
对比 P 值和显著性水平: $\mathrm{P}$ 值 0.9614 远大于 0.05 , 这说明观察到样本均值 99.98 克或更极端值的情况非常常见 (有 $96.14 \%$ 的概率)。
-
可以把 P 值想象成一种“惊讶度”的测量。如果 P 值很小(比如小于 0.05),意味着观察到的结果让我们非常惊讶,原假设可能不成立。但在这里,P 值很大,表示我们并不惊讶于这样的结果,所以我们相信包装机的平均装袋质量仍然是 100 克。
 相关性分析
相关性分析
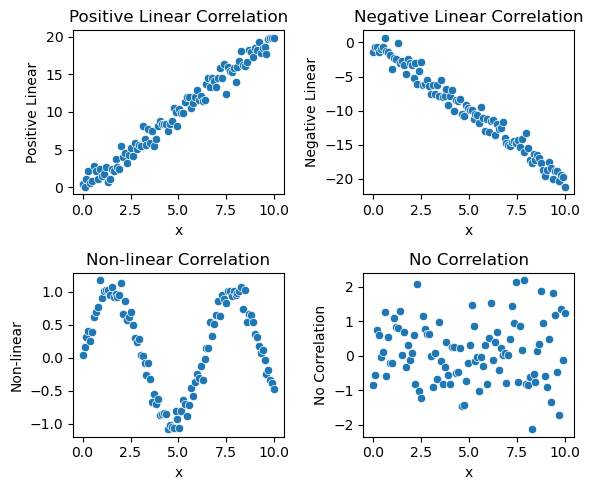
相关性关系(Correlational Relationship)描述的是两个变量之间的线性关系的强度和方向,但不涉及因果关系。
例如,假设有关于人类的身高和鞋码的数据,虽然可能发现这两者之间有正相关,但这并不意味着身高决定了鞋码,或鞋码决定了身高。
- 相关关系的类型:
①根据涉及变量的个数不同分为:单相关和复相关。
②根据变化方向不同分为:正相关和负相关。
③根据相关程度不同分为:完全相关,不完全相关和无相关。
④根据变化形式不同分为:线性相关和非线性相关。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# 设置数据
np.random.seed(42)
x = np.linspace(0, 10, 100)
y1 = 2 * x + np.random.normal(0, 1, 100) # 正相关
y2 = -2 * x + np.random.normal(0, 1, 100) # 负相关
y3 = np.sin(x) + np.random.normal(0, 0.1, 100) # 非线性相关
y4 = np.random.normal(0, 1, 100) # 无相关
# 创建一个DataFrame
data = pd.DataFrame({
'x': x,
'Positive Linear': y1,
'Negative Linear': y2,
'Non-linear': y3,
'No Correlation': y4
})
# 绘制图形
fig, axs = plt.subplots(2, 2, figsize=(6, 5))
# 正相关
sns.scatterplot(x='x', y='Positive Linear', data=data, ax=axs[0, 0])
axs[0, 0].set_title('Positive Linear Correlation')
# 负相关
sns.scatterplot(x='x', y='Negative Linear', data=data, ax=axs[0, 1])
axs[0, 1].set_title('Negative Linear Correlation')
# 非线性相关
sns.scatterplot(x='x', y='Non-linear', data=data, ax=axs[1, 0])
axs[1, 0].set_title('Non-linear Correlation')
# 无相关
sns.scatterplot(x='x', y='No Correlation', data=data, ax=axs[1, 1])
axs[1, 1].set_title('No Correlation')
plt.tight_layout()
plt.show()
皮尔逊相关系数(Pearson Correlation Coefficient)
Pearson correlation coefficient 用于总体(population)时记作 $\rho$ (population correlation coefficient), 给定两个随机变量 X,Y, $\rho$ 的公式为:
$$
\rho_{X, Y}=\frac{\operatorname{cov}(X, Y)}{\sigma_X \sigma_Y}
$$
其中: $\operatorname{cov}(X, Y)$ 是 $X, Y$ 的协方差; $\sigma_X$ 是 $X$ 的标准差; $\sigma_Y$ 是 $Y$ 的标准差。
用于样本(sample)时记作 $r$ (sample correlation coefficient, 给定两个随机变量 $X, Y$, $r$ 的公式为:
$$
r=\frac{\sum_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{\sqrt{\sum_{i=1}^n\left(X_i-\bar{X}\right)^2} \sqrt{\sum_{i=1}^n\left(Y_i-\bar{Y}\right)^2}}
$$
其中: $n$ 是样本数量; $X_i, Y_i$ 是变量 $X, Y$ 对应的 $i$ 点观测值; $\bar{X}$ 是 $X$ 样本平均数, $\bar{Y}$ 是 $Y$ 样本平均数。
这里解释一下什么叫做协方差:统计学上用方差和标准差来度量数据的离散程度,但是方差和标准差是用来描述一维数据的(或者说是多维数据的一个维度),现实生活中常常会碰到多维数据,因此人们发明了协方差(covariance),用来度量两个随机变量之间的关系。仿照方差的公式来定义协方差:(这里指样本方差和样本协方差)。
方差:
$$
s^2=\frac{1}{n-1} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2
$$
协方差:
$$
\operatorname{cov}(X, Y)=\frac{1}{n-1} \sum\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)
$$
-
因为这里是计算样本的方差和协方差, 因此用 $n-1$ 。之所以除以 $n-1$ 而不是除以 $n$, 是因为这样能使我们以较小的样本集更好地逼近总体, 即统计上所谓的“无偏估计”。
-
协方差如果为正值, 说明两个变量的变化趋势一致;
-
如果为负值, 说明两个变量的变化趋势相反;
-
如果为 0 , 则两个变量之间不相关 (注: 协方差为 0 不代表这两个变量相互独立。不相关是指两个随机变量之间没有近似的线性关系, 而独立是指两个变量之间没有任何关系)。
-
但是协方差也只能处理二维关系, 如果有 $n$ 个变量 $X_1, X_2, \cdots X_n$, 那怎么表示这些变量之间的关系呢?
- 解决办法就是把它们两两之间的协方差组成协方差矩阵 (covariance matrix)。
-
最后强调一下 $\mathrm{p}$ 的意义:
- $\mathrm{p}$ 的取值在-1 与 1 之间。取值为 1 时, 表示两个随机变量之间呈完全正相关关系;
- 取值为 -1 时, 表示两个随机变量之间呈完全负相关关系;
- 取值为 0 时,表示两个随机变量之间线性无关。
- 不同 $\mathrm{p}$ 取值下的散点图案例如下图所示。
# Generate example data for different Pearson correlation coefficients
np.random.seed(0)
# Pearson correlation coefficients: 1, 0.5, 0, -0.5, -1
correlations = [1, 0.5, 0, -0.5, -1]
data = {}
for p in correlations:
x = np.linspace(0, 10, 100)
if p == 1:
y = x
elif p == -1:
y = -x
elif p == 0:
y = np.random.uniform(0, 10, 100)
else:
y = p * x + np.random.normal(0, 1, 100) * np.sqrt(1 - p**2)
data[p] = (x, y)
# Improved visualization
fig, axes = plt.subplots(1, 5, figsize=(25, 5), sharex=True, sharey=True)
fig.suptitle('Scatter Plots for Different Pearson Correlation Coefficients', fontsize=16)
for i, p in enumerate(correlations):
x, y = data[p]
axes[i].scatter(x, y, color='blue')
axes[i].set_title(f'p = {p}')
axes[i].set_xlabel('x')
if i == 0:
axes[i].set_ylabel('y')
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()

热力图
 热力图(Heatmap)
热力图(Heatmap)
热力图使用颜色梯度来表示数据的不同值。通常,颜色从冷色(如蓝色)到暖色(如红色)逐渐变化,以显示数据值从低到高的变化。:在统计分析中,热力图可以用来展示变量之间的相关性。具体来说:
-
计算相关系数矩阵:首先,计算多个变量之间的皮尔森相关系数,得到一个相关系数矩阵。矩阵中的每个元素表示两个变量之间的相关系数。
-
颜色编码:将相关系数矩阵中的值通过颜色编码显示在热力图中。通常,正相关用暖色表示(如红色),负相关用冷色表示(如蓝色),无相关或低相关用中性色表示(如白色或灰色)。
-
解释热力图:通过观察热力图,可以直观地看出变量之间的相关性强度和方向。例如,颜色越接近红色,表示变量之间正相关性越强;颜色越接近蓝色,表示变量之间负相关性越强。
对于机器学习和数据挖掘任务,可以根据热力图结果进行特征选择和降维,以提高模型性能和减少计算复杂度。例如:
- 选择与目标变量高度相关的特征作为模型输入。
- 删除高度相关(共线性)的特征,以避免多重共线性问题。
除了可视化特征相关性以外,热力图也通常用来展示数据的强度、密度或值的分布。它通过颜色的变化来表示数据值的大小或密度,从而使人们能够直观地识别出数据的模式和趋势。例如:
- 在地理信息系统中,热力图可以用来展示地理区域内的某些现象的密度,如犯罪率、房价、交通流量等。
- 商业分析:企业可以使用热力图来分析销售数据、市场活动的效果、客户行为等,从而发现潜在的商业机会和问题。
- 在网站分析中,热力图可以显示用户在网页上的点击热区和浏览热区,帮助网站优化。
- 等等
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
# 生成示例数据
data = np.random.rand(10, 12)
# 创建热力图
sns.heatmap(data, annot=True, cmap='coolwarm')
# 显示图表
plt.show()
 Credits
Credits
- Icons made by Becris from www.flaticon.com
- Icons from Icons8.com - https://icons8.com
- Datasets from Kaggle - https://www.kaggle.com/
- Examples and code snippets were taken from "Hands-On Machine Learning with Scikit-Learn and TensorFlow"
- Tal Daniel
作者
arwin.yu.98@gmail.com