SphereNet

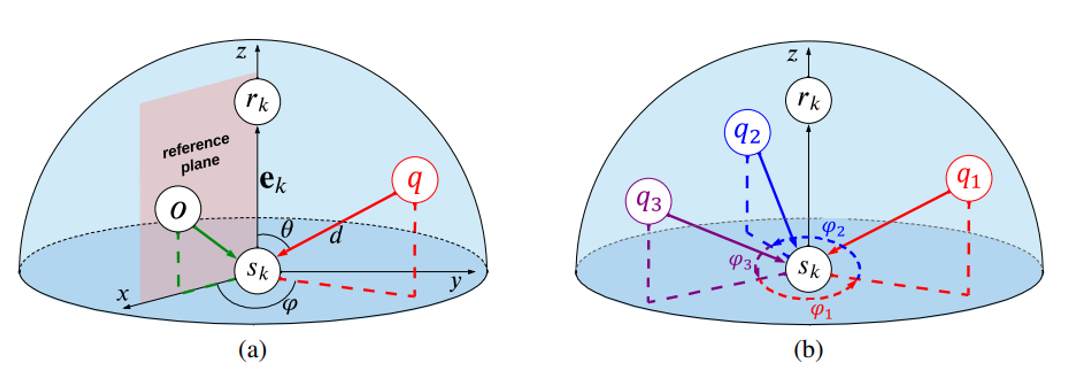
为了更好的描述解释SphereNet的二面角计算方式，我们首先正式定义一个三维分子图，通常表示为一个四元组\(G=(u,V,E,P)\)。其中\(u\in R^{d_{u}}\)是分子图的全局特征向量。$ V=\left\{\boldsymbol{v}_{i}\right\}_{i=1}^{n} $是原子特征集，其中每个\(v_{i}\in R^{d_{\nu}}\)是原子i的特征向量。$E = \left\{ (e_k, r_k, s_k)\right\}_{k=1}^{m}$是边集，其中每个\(e_k\in\mathbb{R}^{d_c}\)是特征向量，\(r_{k}\)是接收原子的索引，而\({s_{k}}\)是发送边k的原子的索引。$P= \left\{ p_h\right\}_{h=1}^{n}$是包含每个原子三维空间信息的三维笛卡尔坐标集。另外，我们使用$E = \left\{ (e_k, r_k, s_k)\right\}_{k=1}^{m}$表示指向原子i的边集，\(N_{i}\)表示进入原子i 的节点的索引集。信息传递过程后的输出包括更新的全局特征向量\(u^{^{\prime}}\in R^{d_u}\)、更新的原子特征$V' = \{ v_i' \}_{i=1}^{n}$和更新的边$\boldsymbol{E}' = \{ (\boldsymbol{e}_k', r_k', s_k') \}_{k=1}^{m}$，SphereNet的二面角计算方式如图1所示。

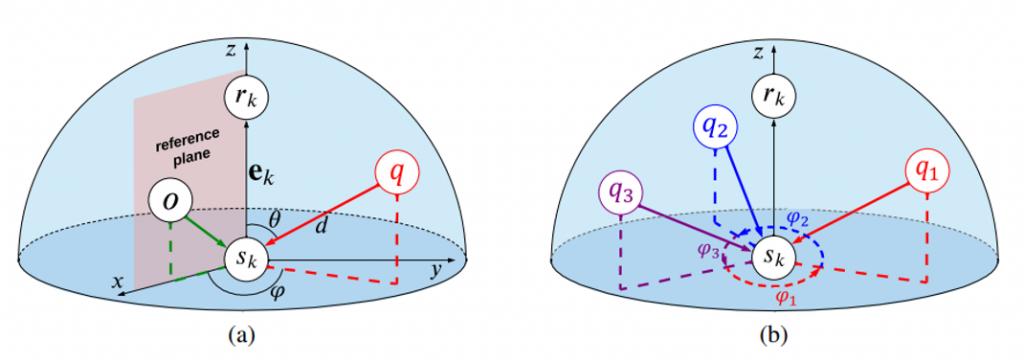
如图1(a)所示，此时的目标是更新原子\(r_{k}\)的嵌入。具体来说，通过先聚合其邻居原子\(s_{k}\)的邻居信息，得到聚合结果\(e_{k}\)来更新原子\(r_{k}\)的嵌入。消息\(e_{k}\)是基于\(E_{s_{\dot{\kappa}}}\)，即所有指向原子\(s_{k}\)的进入消息集合更新的。此时，可以定义一个局部笛卡尔坐标系，其中\(s_{k}\)作为原点，\(e_{k}\)的消息方向作为z轴，定义原子\(s_{k}\)的一个邻原子O作为参考平面，该平面由三个原子\(s_{k},r_{k}\)和O形成，进一步的定义原子O和\(s_{k}\)的投影为x轴。对于原子q，它的位置由图1(a)所示的元组\((d,\theta,\phi)\)唯一定义。具体来说：d确定了它与原子\(s_{k}\)的距离， \(\theta \)指定了它与\(r_{k}\)的夹角，\(\phi \)由定义的参考平面和由原子\(s_{k},r_{k}\)和q构成的平面之间的二面角。这是一种典型的极坐标定义方式，可以全面的表示距离、夹角和二面角信息。

进一步的，原子\(s_{k}\)通常可能有几个邻接原子，表示为\(q_1,\ldots,q_t\)。SphereNet基于极坐标的方式使得计算这些原子的二面角很容易的。具体来说，将所有的t个原子投影到垂直于\(e_{k}\)并与之交叉的平面上来计算二面角。在这个平面上，二面角是以预定义的方向形成的，如逆时针方向。这样做的话，任意一个原子自然就成为其下一个原子的参考原子。值得注意的是，这些t扭转角的总和是\(2\pi \)。一个简化的案例如图1(b)所示，原子\(s_{k}\)有三个邻接原子\(q_1,q_2\)和\(q_3\)，此时可以定义\(q_3\)是\(q_1\)的参考原子，它们形成\(\phi_{1}\)；同理，\(q_1\)是\(q_2\)的参考原子，它们形成\(\phi_{2}\)；同样，\(q_2\)是\(q_3\)的参考原子，它们形成\(\phi_{3}\)。很明显，\(\phi_{1},\phi_{2}\)和\(\phi_{3}\)的总和是\(2\pi \)。由于二面角是相对定义的，初始参考邻居可以任意选取，这不会影响信息传递方案的输出。值得注意的是，通过设计每个原子作为下一个原子的参考原子，这其中隐式的对不变性进行了有效的实现，这是因为参考原子是自然相对的，并不会因为取的初始参照点不同而影响聚合后消息传递的结果。

实际上，SphereNet基于极坐标的方式使得计算二面角是一种简化的更高效的计算方式。在传统的计算方式中，计算二面角（扭转角）通常涉及四个依次相连的原子。传统方法会直接根据这四个原子的三维坐标来计算二面角。这种计算方式虽然直接，但涉及到复杂的几何和三角函数导致计算成本急剧上升。SphereNet采用了投影的方式来计算二面角。这里的“投影”通常是指将这四个原子中的两个（或更多）投影到一个特定的平面，可以将求二面角问题转化为求夹角问题，进而减少计算每个二面角时的计算量。从另一个角度来说，在不投影的情况下，每个邻居间的二面角都需要单独计算，这会导致大量重复计算。而在投影方法中，由于所有邻居都相对于一个共同的参考平面来考虑，这就减少了需要独立计算的次数。