Gemnet

GemNet专门设计用于精准预测分子之间的相互作用，相比之前广泛使用的DimeNet，GemNet通过引入几何二面角信息，使其能够更好的捕捉原子之间复杂的空间关系，考虑它们的位置和类型。

1.1 引入二面角信息

对比DimeNet的消息传递机制，GemNet 的思路比较好理解，既然在DimeNet中，引入方向性的夹角消息传递能够提升精度，那么引入更高维的二面角信息理论上应该能更进一步，如图1所示。

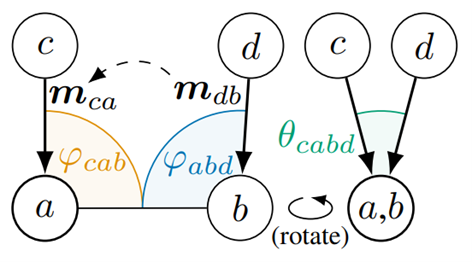
（1）角度表示：图1中展示了三种角度类型：\(\phi_{\mathrm{cab}},\phi_{\mathrm{abd}}\)和二面角\(\theta_{\mathrm{cabd}}\)。这些角度被用来更新原子a和b之间的嵌入\(m_{\mathrm{ca}}\)和\(m_{\mathrm{db}}\)。

（2）二面角的可视化：当分子被旋转使得原子a和b重合时，二面角\(\theta_{\mathrm{cabd}}\)变得可见。二面角是由四个原子a,b,c和d形成的，它关乎两个平面之间的角度，这在化学结构中非常重要，因为它影响了分子的形状和功能。

GemNet中，上述角度信息的公式化表述如公式1、2、3所示，每个公式都定义了特定的数学函数，用于计算原子间相互作用的几何特征。

\(\boldsymbol{e}_{{_{{\mathrm{RBF},n}}}}(x_{{_{{\mathrm{db}}}}})=\sqrt{\frac{2}{c_{{_{{\mathrm{emb}}}}}}}\frac{\sin(\frac{n\pi}{c_{{_{{\mathrm{emb}}}}}}x_{{_{{\mathrm{db}}}}})}{x_{{_{{\mathrm{db}}}}}}\)

\(e_{\mathrm{CBF,ln}}(x_{\mathrm{ba}},\varphi_{\mathrm{abd}})=\sqrt{\frac2{c_{\mathrm{int}}^3j_{l+1}^2(z_{\mathrm{ln}})}}j_l(\frac{z_{\mathrm{ln}}}{c_{\mathrm{int}}}x_{\mathrm{ba}})Y_{\mathrm{l0}}(\varphi_{\mathrm{abd}})\)

\(e_{\mathrm{SBF,lnm}}(x_{\mathrm{ca}},\varphi_{\mathrm{cab}},\theta_{\mathrm{cabd}})=\sqrt{\frac2{c_{\mathrm{emb}}^3j_{l+1}^2(z_{\mathrm{ln}})}}j_l(\frac{z_{\mathrm{ln}}}{c_{\mathrm{emb}}}x_{\mathrm{ca}})Y_{\mathrm{lm}}(\varphi_{\mathrm{cab}},\theta_{\mathrm{cabd}})\)

公式1称为径向基函数，其中\(e_{\mathrm{RBF},n}(x_{\mathrm{db}})\)是第n个径向基函数，用于编码两个原子d和b之间的距离\(x_{\mathrm{db}}\)。\(c_{\mathrm{emb}}\)是归一化常数，用于调整函数的周期性。公式1的作用是捕捉原子对之间的距离信息，它通过正弦函数形式的径向基函数来表示原子间距的信息，并将该信息编码为神经网络可以处理的形式，这种编码对于理解原子对之间的相互作用是重要的。

公式2称为复合基函数（Continuous Filter，CBF），这个表达式结合了球贝塞尔函数\(j_{l}\)和第l阶的球谐函数\(Y_{_{l 0}}\)，以编码原子b和a之间的距离\(x_{\mathrm{ba}}\)，以及它们与第三个原子d形成的角度\(\varphi_{\mathrm{abd}}\)。\(c_{\mathrm{int}}\)是另一个归一化常数，而\(z_{ln}\)表示l阶球贝塞尔函数的第n个零点。公式2结合了球贝塞尔函数和球谐函数，它的作用是捕捉原子三元组之间的角度关系，用于表征由三个原子构成的角度特征，这些信息对于定义分子结构中的角度依赖性特征至关重要。

公式3称为结构基函数（Structural Basis Function，SBF），这个公式用于编码原子c和a之间的距离\(x_{\mathrm{ca}}\)，以及它们与其他两个原子b和d形成的角度\(\varphi_{\mathrm{cab}}\)和二面角\(\theta_{\mathrm{cabd}}\)。这里使用了l阶球贝塞尔函数和l阶m次球谐函数\(Y_{\mathrm{lm}}\)。类似于CBF，SBF的作用是通过考虑更多的角度信息（如二面角）来编码原子四元组间的空间关系，这种复合的基函数允许模型捕捉分子结构的更复杂几何特征，如扭曲和立体排列。

值得注意的是，在公式3中，球谐函数的参数m，当m=0时，球谐函数\(Y_{l}^{m}\left(\theta,\varphi\right)\)只依赖于极角\(\theta \)，与方位角\(\varphi \)无关。这意味着函数在方位角\(\varphi \)方向上是对称的，即在绕z轴旋转时保持不变。而且，公式2的主要作用是衡量角度信息，对于这种简单的角度信息描述，一个基本的对称性分量就足够描述了。另一方面，在公式3中，其主要目的是衡量二面角信息，二面角更为复杂，因为它涉及三个平面之间的角度。因此，我们需要捕捉更多的角度信息，这需要球谐函数的多个分量。具体来说，球谐函数\(Y_{l}^{m}\left(\theta,\varphi\right)\)中的m取值范围为 -l到l ，以捕捉到所有可能的对称性和角度变化。

1.2 GemNet消息传递机制

GemNet的消息传递机制是通过加权和组合前面提到的基函数来构造的，这些消息将在图神经网络中流动。消息传递方案负责聚合和更新节点（原子）的特征信息，从而允许模型学习和预测复杂的分子性质，几何消息传递的方案如下公式：

1.3 模型结构

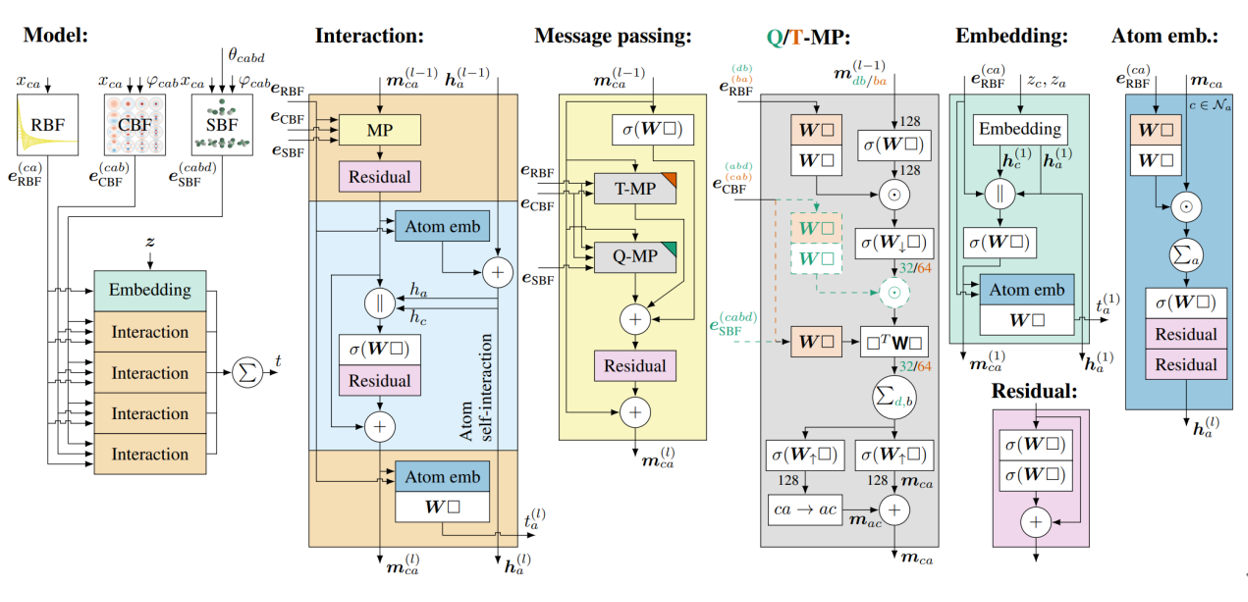
GemNet的模型整体结构如图2(a)所示，DimeNet的模型整体结构如图2 (b)所示。

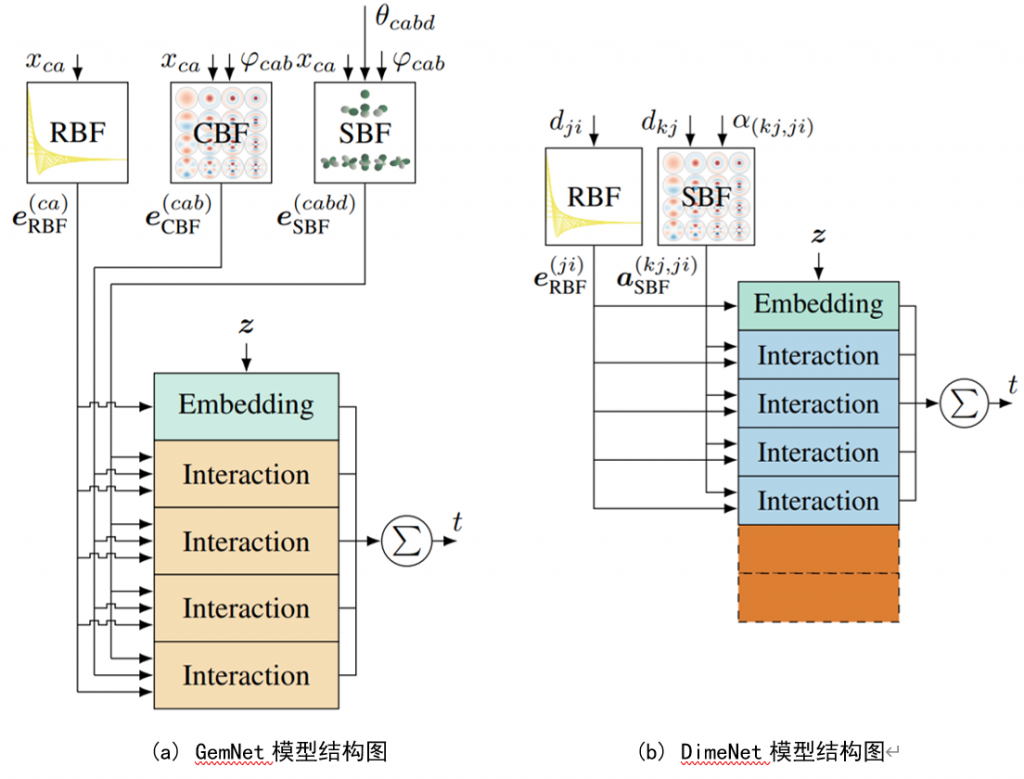
从图2可以看出，两个模型整体的结构很相似，都是一个嵌入层（Embedding）后跟了四个信息交互层（Interaction）做进一步的信息处理，然后把每个交互层处理后的结构求和作为模型最终的输出结果。

不同的是，GemNet通过引入二面角\(\theta_{\mathrm{cabd}}\)的信息，进一步增强了模型处理复杂分子结构的能力。二面角是分子结构中四个原子形成的两个平面之间的夹角，是描述分子空间形状的重要参数之一。在分子动力学和结构生物学中，二面角对于理解分子如何折叠和相互作用至关重要。GemNet的嵌入层（Embedding）如图3(a)所示，DimeNet的嵌入层（Embedding）如图3(b)所示。

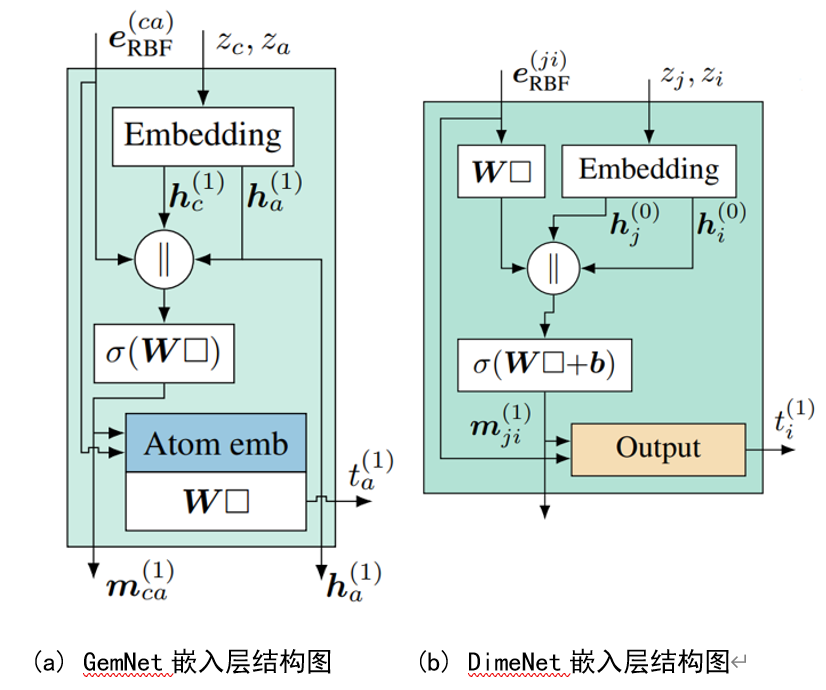
从图3可以看出，两个模型接受的输入数据的一样的，都是基于径向函数的距离信息和两点自身的特征向量。对比DimeNet，GemNet在接下来的操作中，\(e_{\mathrm{RBF}}\)没有经过线性变换，而是直接与节点向量\(\boldsymbol{h}_{c}\)和\(\boldsymbol{h}_{a}\)进行拼接，节点向量\(\boldsymbol{h}_{a}\)除了参与拼接操作外，此时也会复制一份直接作为Embedding层的输出。而拼接后的信息则经过一个神经网络做进一步的学习映射，得到的结果\(m_{\mathrm{ca}}^{(1)}\) 作为该嵌入模块送入后续交互模型的信息。这一步与DimeNet相同，不同的是，该嵌入模块的输出结果t不是m经过Output层得到的，而是经过Atom emb层计算得到的，Output层和Atom emb层如图4所示。

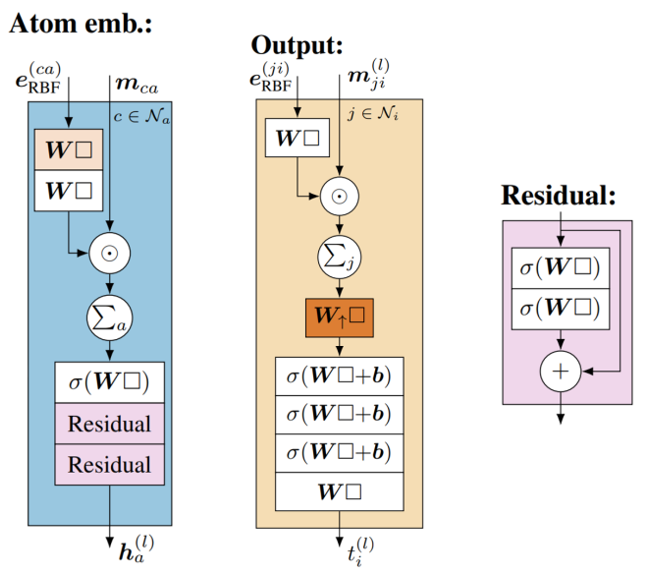
可以看出，只是GemNet的嵌入模块比DimeNet的嵌入模块多了一些线性层与残差结构而已。

GemNet的交互模块如图5所示。

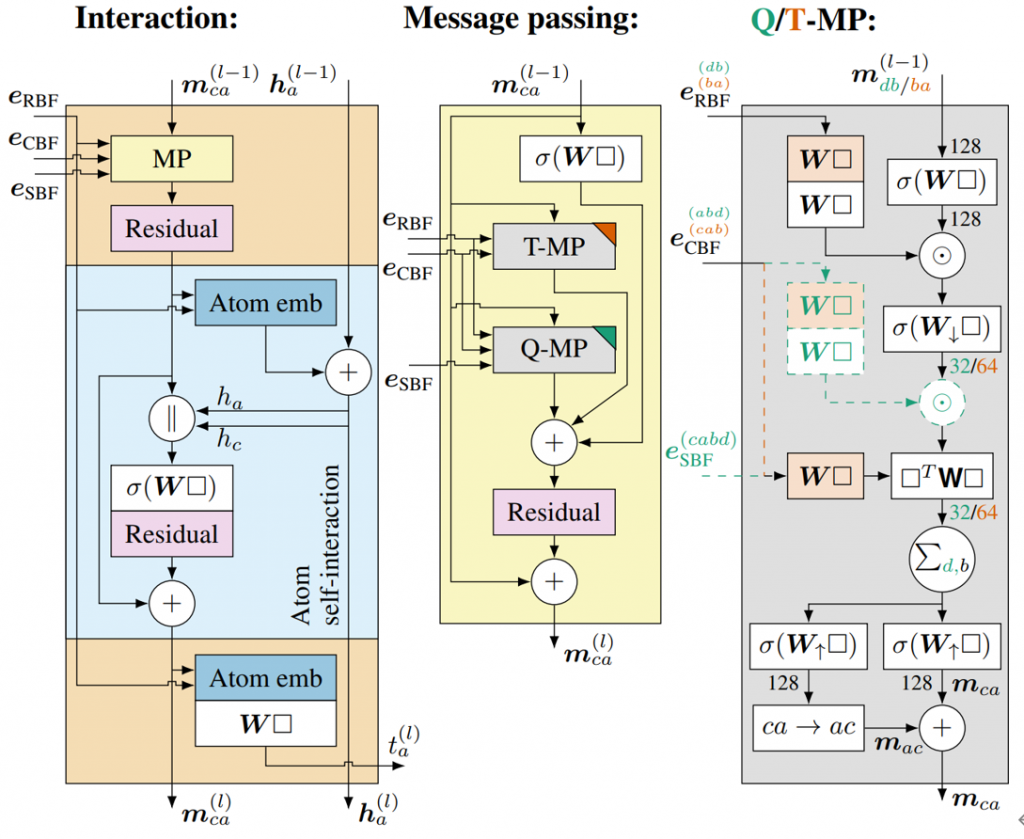
在交互模型的上层，可以发现\(m_{ca}^{(l-1)}h_{a}^{(l-1)}\)的输入，它们分别代表上一层传递下来的消息和原子的特征向量。消息传递（MP）模块利用基于不同阶的球谐基函数\(e_{\mathrm{CBF}}\)和\(e_{\mathrm{SBF}}\)，以及基于径向基函数的\(e_{\mathrm{RBF}}\)来处理这些消息，以便捕获原子间的角度和距离信息。经过MP模块和残差连接（Residual）后，消息\(m_{ca}\)被更新。

MP模块（Message passing）的结构如图5的中间部分，输入信息\(m_{ca}^{(l-1)}\)从上一层传来的消息，是原子c到原子a的消息嵌入。它包含了先前层中两原子之间相互作用的信息。该信息在被处理之前会复制一份用于MP模块底部的残差连接，防止深层网络中出现梯度消失或梯度爆炸的问题。

T-MP和Q-MP这两个模块代表了不同类型的消息传递方式。Q-MP代表“四元组”消息传递，处理四个原子间（即二面角）的相互作用；而T-MP可代表“三元组”消息传递，处理三个原子间（即角度）的相互作用。这些模块均使用球谐基函数和径向基函数的信息来更新消息，T-MP和Q-MP这两个模块详见图5的右侧。

以Q-MP为例，输入特征包括原子对特征\(e_{\mathrm{RBF}}\)，原子三元组夹角特征\(e_{\mathrm{CBF}}\)，原子四元组二面角特征\(e_{\mathrm{SBF}}\)以及上一层的消息m。消息m首先经过神经网络层的处理，这一步将输入特征m映射到一个新的表示空间。然后与经过线性变化后的原子对特征\(e_{\mathrm{RBF}}\)进行逐元素乘，目的是让消息m的更新考虑原子对的距离特征。接下来，再次经过神经网络层的处理，与经过线性变化后的三元组夹角特征\(e_{\mathrm{CBF}}\)进行逐元素相乘，这一步的目的是让消息m的更新进一步考虑方向夹角的特征。下一步，计算后的结果会与四元组二面角特征\(e_{\mathrm{SBF}}\)一起送入双线性层做进一步的特征融合，通过求和聚合所有相关d和b的处理后信息。聚合后的消息被复制成两份分别送入两个神经网络层做处理，最后相加结果得到最终的输出，即更新后的消息m。

值得注意的是，\(ca\to ac\)这一步骤指的是将原子对的方向嵌入从一个方向转换到相反方向的过程。这是因为消息传递通常是方向性的，这意味着从原子c到原子a的信息流是与从原子a到原子c的信息流不同的。然而，由于物理相互作用的对称性，原子c对a的影响在本质上与原子a对c的影响是相同的，只是方向相反。GemNet在更新方向性嵌入\(m_{ca}\)时，它们也会同时考虑对称的嵌入 。为了避免重复计算，GemNet 通过简单的重索引操作来区分方向。这样做可以保持两个方向嵌入之间的区别，同时避免不必要的计算负担。因此，\(ca\to ac\)的作用是在模型内部执行一个转换，确保对于每对原子，信息在两个方向上都得到更新，而不需要进行两次独立的计算。这不仅提高了计算效率，还保持了模型对分子内相互作用对称性的考虑。

在MP模块的最后，T-MP、Q-MP和经过神经网络层处理的\(m_{ca}^{(l-1)}\)将进行相加，送入残差模型做进一步的计算处理得到MP模型的计算结果，即更新信息后的\(m_{ca}^{(l)}\)。在MP模块计算结束后，计算结果会进一步的送入原子自相互作用模块（Atom Self-interaction），其结构如图6所示。

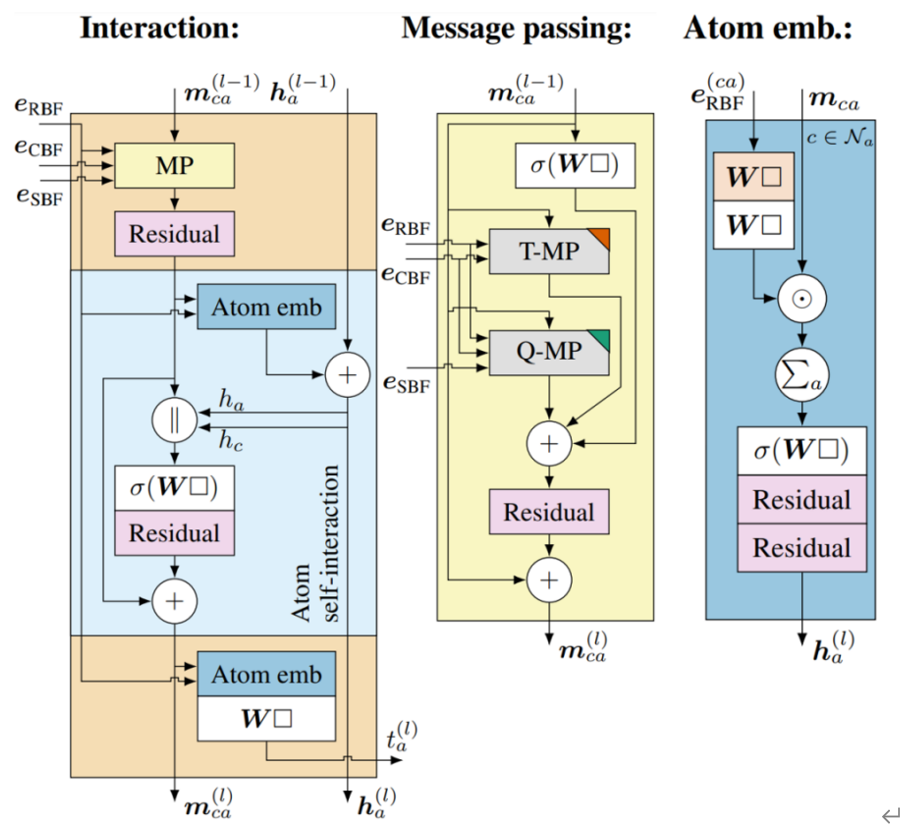
由图6可知，MP模块的计算结果将复制成两份进入两个分支。其中一个分支将与距离信息\(e_{\mathrm{RBF}}\)一起被送入Atom emb层进行进一步的的学习映射，Atom emb层的内部实现就是一些简单的神经网络层，这种形式的消息传递仅考虑每个原子a与其直接相邻的邻居c之间的相互作用。Atom emb层的计算结果将与 相加得到更新后的原子a的特征表示 。MP模块计算的另一个分支将与原子a和c的特征向量进行拼接，然后送入一个神经网络层和残差模块进行进一步的信息处理，得到的结果 ，作为当前模块的计算结果。同时，也被复制成一份，经过Atom emb层和线性层的处理作为当前模型的输出 。值得注意的是，MP的计算结果与原子a和c的特征向量进行拼接后送入一个神经网络层，这一步是不涉及任何空间信息的，只有原子自身信息的交互，这也是该模块被称为原子自相互作用模块的原因。

GimNet的模型架构与细节如图7所示。

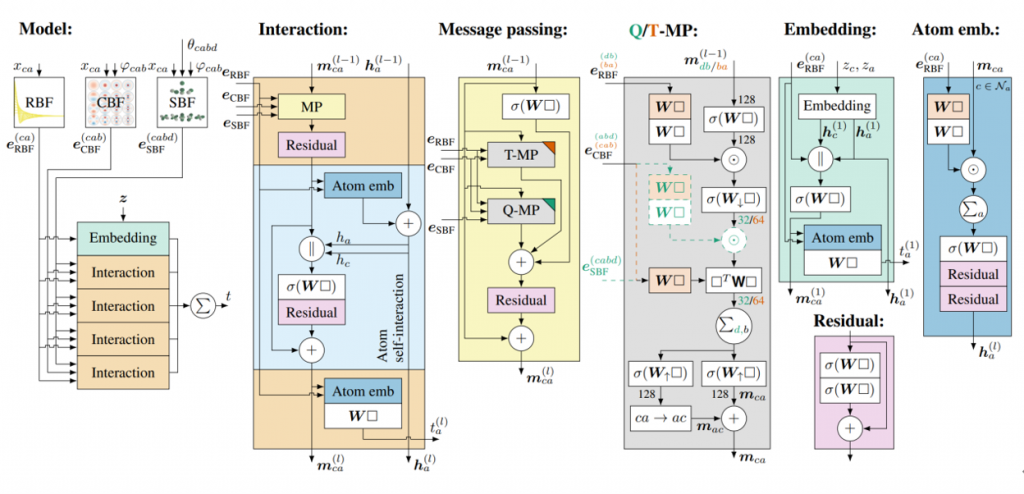
总的来说，对比DimeNet++，GimNet通过引入二面角的信息，以便更好的对几何结构进行建模。在交互模块中，存在三种信息交互方式。第一种是原子自相互作用模块（Atom Self-interaction），仅对原子本身的特征向量进行交互更新，不涉及空间属性；第二种是MP模块中的T-MP，通过对相邻的原子三元组基于径向模型和球谐函数进行建模，引入距离和夹角信息，以更好的进行几何结构的表示；第三种是MP模块中的Q-MP，与T-MP类似，通过引入二面角信息来更好的表示几何空间结构。模型最后的输出方式与DimeNet++类似，通过对所有交互模块的结果求和得到模型最终的输出结果。